Bez czwórkwadratów

5 listopada 2022
Marek Penszko

W regułach kilkunastu rodzajów zadań (zwłaszcza tych z japońskim rodowodem), polegających na dzieleniu pokratkowanego diagramu na części, znajduje się warunek, aby wszystkie lub niektóre z tych części nie obejmowały kwadratu złożonego z czterech kratek (2×2). Warunek bywa obecny po to, by rozwiązanie było jedno, ale zwykle jest bardziej istotny i wielokrotnie wykorzystywany w trakcie rozwiązywania, jak na przykład w zapewne najpopularniejszym typie zadania, który go zawiera – nurikabe. Niekiedy zakaz obecności czwórkwadratu pojawia się jako dodatek, tworzący wariant zadania. Tak właśnie jest w przypadku jednej z odmian pokropki.
Przypomnijmy: pokropka polega na wrysowaniu w siatkę kwadratową linii łamanej zamkniętej, czyli pętli, pokrywającej się z liniami siatki i nie goszczącej dwukrotnie w tym samym punkcie; każda cyfra oznacza, ile boków zawierającej ją kratki (jeden, dwa, trzy lub zero) powinno być fragmentami łamanej.
Tę instrukcję uzupełnia wspomniany warunek: wewnątrz pętli nie powinno być kwadratu 2×2. Albo inaczej: pętla nie może otaczać żadnej „wolnej” niebieskiej kropki, czyli nie należącej do pętli.
Przykład:

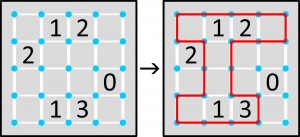
Zadanie:

Jako rozwiązanie wystarczy podać liczbę błękitnych kropek nie objętych pętlą.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.