Kwartet kwintetów

Wiele formalnie prostych, schematycznych, niewyszukanych łamigłówek liczbowych bywa mimo to (a może właśnie dlatego) wciągających. W pierwszej chwili na myśl przychodzą zadania typowe dla testów Mensy w rodzaju „uzupełnij właściwą liczbą…” (jakiś układ liczb lub ciąg). Niektórzy wytrwale ślęczą nad takimi drobiazgami – a te mogą stawiać zaciekły opór. Nierzadko wywołują też „burzliwe” dyskusje, gdy okazuje się, że na upartego rozwiązań można podać więcej niż jedno autorskie. Takie zadania bywają zwykle prezentowane w jakoby uatrakcyjniającej je formie graficznej. Oto przykład.

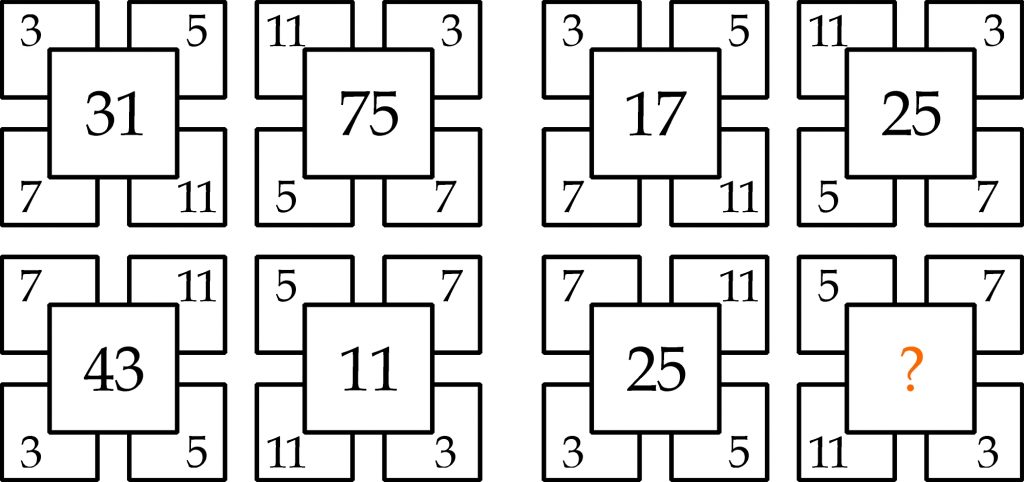
Lewy rysunek to wzór: liczby rozmieszczone w czterech kwintetach kwadratów – w każdym kwintecie zgodnie z taką samą zasadą. Tego samego rodzaju zasada (ale nie dokładnie taka sama) obowiązuje w kwintetach na prawym rysunku, ale w środku ostatniego jest znak zapytania. Należy go zastąpić właściwą liczbą.
Bez dodatkowych informacji zadanie jest benedyktyńskie i raczej odstręcza niż wciąga. Można się wprawdzie domyślić, że liczba w środku każdego kwintetu jest wynikiem działań na otaczających ją czterech liczbach, których wartości w kwintetach są niezmienne, ale rozmieszczenie różne.
Kluczem do rozwiązania może być następująca wybrakowana równość, dotycząca pierwszego kwintetu lewego diagramu:
11 ? 3 ? 5 ? 7 = 31
Brakuje w nim trzech znaków działania (z zakresu czterech podstawowych) między czterema liczbami i ewentualnie nawiasów, natomiast podana jest kolejność liczb w działaniu, odpowiadająca położeniu małych kwadratów z tymi liczbami (prawy dolny > lewy górny > prawy górny > lewy dolny) i obowiązująca w pozostałych kwintetach.
Teraz już nietrudno uzupełnić podaną równość i upewnić się, że jej schemat jest właściwy, rozwiązując działania odpowiadające trzem pozostałym kwintetom:
11 × 3 + 5 – 7 = 31
7 × 11 + 3 – 5 = 75
5 × 7 + 11 – 3 = 43
3 × 5 + 7 – 11 = 11
Jak widać we wszystkich działaniach obowiązuje nie tylko kolejność liczb zgodna z podaną wyżej kolejnością kwadratów, ale także jednakowy układ znaków (uwzględniając także nawiasy – jeśli się pojawią).
A zatem: jaka liczba powinna zastąpić znak zapytania na powyższym prawym rysunku?

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.

Komentarze

[lukasz_m]

(11 – 7) x 3 + 5 = 17
(7 – 5) x 11 + 3 = 25
(5 – 3) x 7 + 11 = 25
(3 – 11) x 5 + 7 = -33

[xswedc]

-33

(11-7)*3+5 = 17
(7-5)*11+3 = 25
(5-3)*7+11 = 25
(3-11)*5+7 =-33

[izabella]

-33

Mało eleganckie, ale się zgadza. Może jest więcej rozwiązań?

[apartado]

Minus 33.

[Antyp1958]

Schemat Lg-Pg-Ld-Pd

5+3x(11-7)=17
7+3x(11-5)=25
11+7x(5-3)=25
7+5x(3-11)=-33

?=-33

[tomash]

Dobry wieczór,

moja odpowiedź to 5*(3-11) + 7 = -33

3 * (11-7) + 5 = 17
11 * (7-5) + 3 = 25
7 * (5-3) + 11 = 25

Jestem ciekaw czy to jedyna dobra 🙂
Pozdrawiam,

Na razie innej nie znaleziono. Dam znać, gdy się pojawi.
mp

[BartoszC]

Wyszło mi -33. Przykładowe działanie (LG oznacza lewy gór róg, itd.):
PG + LG * (PD – LD)

5 + 3 * (11 – 7) = 17
3 + 11 * ( 7 – 5) = 25
11 + 7 * ( 5 – 3) = 25
7 + 5 * ( 3 – 11) = -33

Można zamienić znaki i dostać inne działanie: PG – LG * (LD – PD). Manipulując kolejnością można otrzymać więcej wersji tego działania, każda dająca wynik -33,
Nie znalazłem żadnego działania nie wykorzystującego nawiasów.

[ersonasolidna]

Znak zapytania powinna zastąpić liczba – 33 (trochę tu mam wątpliwość, bo liczba wychodzi ujemna, ale nie było w zadaniu warunku, że ma być naturalna).

No ale:
(1 1 – 7) × 3 + 5 = 17
(7 – 5) × 11 + 3 = 25
(5 – 3) × 7 + 11 = 25
(3 – 11) × 5 + 7 = – 33

Gdyby okazało się, że ujemna liczba to faktycznie poprawne rozwiązanie, to poniżej dzielę się sposobem dojścia do niego.

Wspomnienie w artykule o „ewentualnych nawiasach” od razu rzuca podejrzenie na rozwiązanie, które rzeczone nawiasy zawiera. Ponieważ 17 jest liczbą pierwszą, nie może to być iloczyn w rodzaju (a+b) × (c-d) lub coś podobnego. Doszedłem do wniosku, że może zostaje iloraz, ale po przemyśleniu wszystkich wielokrotności liczby 17 (51, 85, 119), stwierdziłem, że bardziej prawdopodobny jest jeden z 3 wariantów: (a + b) × c – d, (a – b) × c – d lub (a – b) × c + d. (a + b) × c + d wykluczyłem, bo wtedy te liczby wychodzą zbyt wielkie.

No i okazało się, że pierwszy promyczek nadziei padł przy (7-11)*3-5, co daje -17. Przy obróceniu znaku, czyli -((7-11)*3-5) mamy szukane 17, i faktycznie znajdziemy pozostałe 25 i 25, ale to jest to samo, co bardziej eleganckie (11-7)*3+5=17. Zatem ostatni z 3 wzorców (a – b) × c + d jest tym właściwym.

[xswedc]

@ersonasolidna
Czy rozważałaś, jako mężczyzna, zmianę nicka na ersonasolidny? Wprawdzie byłoby niegramatycznie, ale za to prawdziwiej i bardziej intrygująco…

[ersonasolidna]

@xswedc
Dziękuję, że dałeś mi okazję, aby zwrócić uwagę na (nieświadomego tego faktu) autora tej ksywy, którym jest genialny tłumacz z języka angielskiego – Krzysztof Bartnicki. Bartnickiemu 10 lat pracy zajęło tłumaczenie książki „Finnegans Wake” Jamesa Joyce’a. Tłumaczenie pojawiło się 2012 roku. Sama książka jest generalnie bełkotem i nie ma sensu jej przeczytać, ale warto zestawić obok siebie 2 egzemplarze: oryginał i tłumaczenie. Na pierwszej stronie tytułowy Finnegan jest nazywany „Finnegan, erse solid man”, z którego Bartnicki stworzył „Finnegana, ersonę solidną jak zadko”. „Finneganów Tren”, bo tak brzmi polski tytuł, pełen jest takich smaczków – nie sposób nie zachwycić się kunsztem tłumacza. Więc zachwycałem się, dzieliłem się różnymi fragmentami wśród znajomych z pracy, aż ktoś – gdy zrealizowałem coś w terminie – powiedział mi, że jestem „ersoną solidną jak zadko!” No i tak zostało.

[xswedc]

@ersonasolidna
Więc jednak nie kryje się za tym banalna literówka, lecz ciekawa historyjka kalamburogenna. W innej książce ten sam autor zachęca: „Obnaż ostrza swych definicji” – i właśnie tak zrobiłeś swoim nickiem. Odtąd, już bezstresowo będę czytał twoje wpisy…