Zero dziewięć
Tegoroczny letni „Omnibus” miał spore wzięcie, więc jeśli autor podoła, to w przyszłym roku będzie następny, już szesnasty. Informacje o wzięciu są dla mnie jak zwykle równie miłe, co zaskakujące – głównie dlatego, że zadania w „Omnibusach” do łatwych nie należą, więc jeśli służą zabijaniu czasu, to stanowią zapewne dla części rozwiązujących morderstwa z premedytacją o odcieniu masochistycznym. Ściśle rzecz biorąc, w miarę proste zadania stanowią w tych zeszytach wyraźną mniejszość.
Poniżej dwa przykłady, należące do goszczącego czasem w „Omnibusach” gatunku arytmetyki szkieletowej. Pierwszy zaliczyłbym do wspomnianej prostej mniejszości, drugi – do orzechów ekstremalnej twardości omnibusowej.
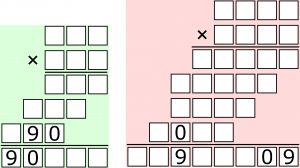
Przypomnę, że chodzi o rozszyfrowanie mnożeń, w słupkowym zapisie których ujawniono tylko cztery cyfry – pozostałe zastąpiono kratkami. Wypada dodać, że pojawienie się jeszcze jakichś zer i dziewiątek w pustych kratkach nie jest wykluczone.

Komentarze
178×511=90958, 9091×1199=10900109
9091
*1199
—–
81819
81819
9091
9091
——–
10900109
Drugie zadanie miodzio, ale przeoczyłem pierwsze zadanko.
Chciałbym to teraz nadrobić, lecz mam zgryz. Znalazłem dwa rozwiązania różniące się o X, gdzie X zapisane w systemach szóstkowym, siódemkowym i ósemkowym, jest w każdym z nich palindromem.
Czy dobrze rozwiązałem to zadanie?
Z jakiegoś powodu Gospodarz wstrzymał mój neutralny komentarz do zadania pierwszego, więc skoro już „po ptakach” ujawniam obydwa rozwiązania:
http://pokazywarka.pl/zero_dziewiec/
Różnica pomiędzy iloczynami to
X=90958-90780=178
178_(10) = 454_(6)
178_(10) = 343_(7)
178_(10) = 262_(8)
Nie sprawdzałem wszystkich liczb trzycyfrowych, ale coś mi podpowiada, że 178 jest jedyną taką liczbą, która ma trzy palindromy w innych systemach. Jeśli to prawda, to można ją uznać za liczbę „prawie ciekawą” (jest taka kategoria? 🙂 ).
Co do rozwiązania obydwóch zadań – kluczem, w moim przypadku była analiza przeniesień. W zadaniu 1: na A3 (nad ósemką) musi być przeniesienie 1, bo w B1 jest 0. Stąd A2 to 8. Mamy więc w wierszu 2 liczbę 890=2*5*89. Jeden z czynników mnożenia to 890/2=445 lub 890/5=178. 445 od razu odpada (dlaczego?), więc to 178. Pozostaje tylko dopasować drugi czynnik. Na D5 musi być 1, aby B3+B2 dało na B1 cyfrę 0. Po krótkim sprawdzeniu okazuje się, że warunki zadania na drugi czynnik spełniają dwie liczby: 510 i 511.
Drugie zadanie rozwiązuje się, co do metody, identycznie. Kluczowe są przeniesienia, z których wynika cała reszta rozwiązania.
Uciekło mi jedno zdanie po „Pozostaje tylko dopasować drugi czynnik”:
Jego pierwszą cyfrą na C5 musi być 5.