Polidoku
Wszystkie łamigłówki, polegające na wpisywaniu cyfr w kratki, w których jako rozwiązanie powstaje kwadrat łaciński, można uznać za spokrewnione z sudoku. Tylko koligacje mogą być bliższe lub dalsze. Ostatnio obracam się wśród bliskich krewnych, których cechą wspólną i ogólną jest podział pokratkowanego diagramu na niewielkie polimina, czyli wielokąty obejmujące kilka kratek. W kratki wpisuje się cyfry zgodnie z regułami, które są cechą specyficzną danego rodzaju zadania. Zapewne najbliższy sudoku jest rodzaj polizadania (polidoku?), którego przykład wygląda tak:
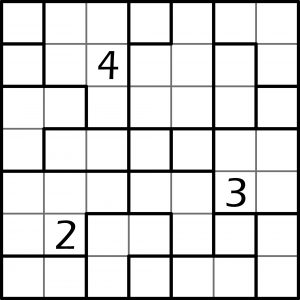
Jak zwykle w kwadracie łacińskim n×n, cyfry od 1 do n (w tym przypadku n=7) należy wpisać w kratki tak, aby w każdym wierszu i w każdej kolumnie występowało siedem różnych cyfr. Zaś warunek ekstra jest następujący: w każdym poliminie, czyli działce otoczonej grubą linią (są wśród nich także samotne kratki, czyli monomina), powinny się znaleźć kolejne cyfry, a więc stanowiące fragment ciągu liczb naturalnych; ich rozmieszczenie w działce może być dowolne (oczywiście z uwzględnieniem nadrzędnej podstawowej cechy kwadratu łacińskiego).
Łamigłówka, jako rodzaj, wydaje mi się ciekawsza niż sudoku, bo jej logika jest bogatsza i bardziej zakręcona.
Powyższe zadanie jest dziełkiem japońskiego speca od łamania głowy Inaby Naoki’ego, więc dwóch rzeczy można być pewnym: jest perfekcyjne autorsko i niełatwe. W rozwiązaniu wystarczy podać cyfry, które znajdą się w rogach diagramu.

Komentarze
Mówi się „nie chwal dnia przed zachodem Słońca”, ale chyba wolno pochwalić łamigłówkę zanim się ją rozwiązało ?.
Jest wyśmienita.
Nie było specjalnie trudne
7132456
1543267
4325671
2671345
5416732
3267514
6754123
76
63
Pozdrawiam 🙂
Czy może się zdarzyć, że dwa przyległe polimina chociaż są rozdzielone, mogą być połączone? Na przykład jedno polimino zawiera (2,3,4) a drugie (1) i przylegają do siebie bokiem?
Oczywiście, to jest możliwe (tak zresztą jest w kilku miejscach w tym zadaniu).
mp
7132456
1543267
4325671
2671345
5416732
3267514
6754123
Znam tę łamigłówkę pod nazwą Renban, mam ją nawet w generatorze łamigłówek, tylko dawno nie rozwiązywałam. Ale teraz dzięki Łamiblogowi przypomniałam sobie, jaka jest fajna, i wygenerowałam kilka trudnych przykładów. Będą wyśmienite na jazdę pociągiem, która mnie dziś czeka 😉
7 1 3 2 4 5 6
1 5 4 3 2 6 7
4 3 2 5 6 7 1
2 6 7 1 3 4 5
5 4 1 6 7 3 2
3 2 6 7 5 1 4
6 7 5 4 1 2 3
7132456
1543267
4325671
2671345
5416732
3267514
6754123
Mniej więcej do połowy (trochę mniejszej) rozwiązywało się płynnie, aż natrafiłem na korek. Od tego momentu rozpatrywałem różne warianty, ale na dalszym etapie zauważyłem przegapiony wcześniej element. A to oznacza, że jutro wracam do zadania i poszukuję jasnej ścieżki od początku do końca 🙂
7663
Na pierwszy rzut oka wydaje się, że jest za mało informacji i da się wydedukować tylko kilka cyfr, ale później okazuje się, że logicznie można wywnioskować wszystko.
„A to oznacza, że jutro wracam do zadania i poszukuję jasnej ścieżki od początku do końca”
Ścieżka istnieje 🙂
Od góry: 7132456; 1543267; 4325671; 2671345; 5416732; 3267514; 6754123.
Ciekawa byłaby wersja „cykliczna”, czyli 1 jako sąsiad 7 i możliwe układy typu 7123, 671.
Pozdrawiam.
@Ola GM
Podziel się przykładami 🙂
Na wyspie Zagadkowej, żyje sobie wiele gatunków drapieżników.
Część z nich to kanibale, czyli w menu takiego gatunku możemy znaleźć tenże gatunek, być może, miedzy innymi gatunkami.
Oczywiście w menu gatunków, które kanibalami nie są, nie odnajdziemy tegoż gatunku.
Po zaobserwowaniu tych faktów, profesor Szaradek postawił następujące pytanie:
Czy istnieje taki podzbiór gatunków, który nie może stanowić menu dla żadnego gatunku ?
😉
A dlaczego nie ma nowego wpisu autora
Z powodu choroby autora wpisy będą przez kilka tygodni pojawiać się mniej więcej dwukrotnie rzadziej
mp
Niby trudne, a w pewnym momencie rozwiązanie jakoś leci samo 🙂
7132456
1543267
4325671
2671345
5416732
3267514
6754123
@Spytko z Melsztyna
> Czy istnieje taki podzbiór gatunków, który nie może stanowić
> menu dla żadnego gatunku ?
Innymi słowy: czy istnieje drapieżnik, którego nikt nie je? Może istnieć. Jest największy, nikt go nie je, on sam tylko zje to i owo. Czy to jest dobra odpowiedź?
@OlaGM:
Niech zapis g1 -> {g2, g3, g4} oznacza, że menu gatunku g1 stanowi podzbiór gatunków {g2, g3, g4}
Dla krótkości zapisu będziemy używać samych liczb.
Tak więc zapis: 2 -> {2,7, 11} oznacza, że 2 jest kanibalem bo zjada 2 ale nie gardzi również 7 i 11.
Natomiast z zapisu 3 -> {2, 5, 9, 13} wynika, że 3 nie jest kanibalem bo w menu nie ma 3.
W ten sposób możemy skonstruować menu dla każdego gatunku.
Po wykonaniu tej pracy stwierdzimy, że użyty przez nas podzbiór N rozpada się a na dwa zbiory KANIBALE i NIEKANIBALE.
Wyobraźmy sobie teraz, że na wyspę zawitał światowej sławy dietetyk i postanowił zreformować nieco zastany porządek.
Upatrzył sobie jakiś gatunek x (np. któregoś kanibala) i postanowił, że od jutra będzie się ten gatunek (x) odżywiał wyłącznie podzbiorem NIEKANIBALI.
Jednak po chwili zastanowienia spostrzegł, że jest to nie możliwe ze względów logicznych. Spróbował więc przyporządkować to menu (podzbiór NIEKANIBALI) innemu gatunkowi y (który tym razem jest niekanibalem).
Z przykrością musiał i tym razem stwierdzić, że jest to również nie możliwe ze względów logicznych.
Załamany czym prędzej opuścił wyspę i zwierzęta żyły długo i szczęśliwie w niezaburzonym środowisku naturalnym.
Ćwiczenie polega na sprawdzeniu niemożliwości przeprowadzenia tej reformy 🙂