Maluch ABC
Zaczynamy od narysowania trójkąta ABC „giganta”. Żeby było elegancko – równobocznego, choć nie jest to konieczne. Następnie dzielimy giganta na mniejsze trójkąty tak, by każde dwa „maluchy” miały albo wspólny bok, albo tylko wierzchołek, albo nie miały nic wspólnego. Inaczej mówiąc, chodzi o to, by bok żadnego malucha nie był częścią boku innego malucha.
Następnie oznaczamy literami A, B, C wszystkie wierzchołki maluchów leżące wewnątrz giganta ABC i na jego bokach. Warunek jest tylko jeden: żaden wierzchołek malucha, znajdujący się na boku x giganta, nie może zostać oznaczony taką samą literą, jaką oznaczony jest wierzchołek giganta leżący naprzeciw boku x.
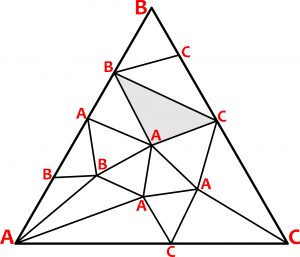
Efekt końcowy może być na przykład taki:
Dlaczego, mimo sporego luzu w oznaczaniu wierzchołków, wśród maluchów zawsze pojawi się przynajmniej jeden trójkąt ABC? – oto jest pytanie. Innymi słowy: czy ktoś potrafi dowieść (możliwie elegancko), że tak być musi?

Komentarze
Wierzchołki maluchów leżące na brzegu trójkąta będziemy określać jako punkty brzegowe/zewnętrzne, pozostałe jako punkty wewnętrzne.
Mówiąc „gigant” będziemy mieli na myśli wielokąt, którego wierzchołkami są wszystkie punkty zewnętrzne (początkowo gigant będzie zdeformowany, tzn. przy niektórych jego wierzchołkach kąt będzie półpełny).
W każdej chwili na brzegu giganta będą wyróżnione trzy punkty A, B i C, o własności podanej w treści zadania jako warunek, tzn. wszystkie wierzchołki giganta znajdujące się na brzegu pomiędzy punktami A i B będą oznaczone jedną z liter A, B (i podobnie dla dwóch pozostałych fragmentów brzegu AC i BC).
Dodatkowo zapis X=A będziemy rozumieli tak, że punkt, który oznaczyliśmy jako X, jest oznaczony literą A (co nie musi oznaczać, że jest to punkt A z podziału brzegu giganta).
W pojedynczym kroku będziemy wyrzucać z giganta jednego malucha, modyfikując brzeg w taki sposób, aby zachowany był warunek podziału brzegu na 3 części.
Niech punkt X jest wierzchołkiem giganta na boku AB znajdującym się najbliżej punktu A. Punkt Y to trzeci punkt malucha o boku AX.
Z giganta usuwamy malucha AXY. Jeśli ten maluch jest ABC, to jest szukanym maluchem.
Mamy 4 możliwości:
– X=A oraz Y leży na brzegu AC. Wtedy usuwamy z brzegu giganta odcinki AX oraz AY oraz dodajemy odcinek XY. Ponieważ usunęliśmy z giganta punkt podziału brzegu A, więc nowym punktem podziału staje się punkt X(=A).
– X=B oraz Y leży na brzegu AC. Jeśli Y=C to maluch AXY jest szukanym maluchem ABC. W przeciwnym przypadku Y=A. Usuwamy z brzegu odcinki AX i AY, dodajemy XY, a nowym punktem podziału brzegu staje się punkt Y(=A).
– X=A oraz Y jest punktem wewnętrznym. Z brzegu usuwamy odcinek AX, dodajemy odcinki AY i XY. Teraz jeśli Y=C, to punkt podziału brzegu A przesuwamy do X(=A). Jeśli natomiast Y=B lub Y=A, to punkt podziału zostaje w oryginalnym miejscu.
– X=B oraz Y jest punktem wewnętrznym. Jeśli Y=C, to AXY jest szukanym maluchem. W przeciwnym przypadku z brzegu usuwamy odcinek AX, dodajemy odcinki AY i XY. Punkt podziału brzegu pozostaje w punkcie A.
W ten sposób, jeśli początkowo było n maluchów, w każdym kroku usuwamy jednego malucha. Albo w którymś kroku znajdziemy malucha ABC, albo po n-1 krokach nasz gigant stanie się maluchem. Będzie on oczywiście maluchem ABC, to zawsze na brzegu giganta były punkty A, B i C.
To jest znany fakt, tzw. lemat Spernera (wykorzystywany w dowodzie tw. Brouwera o punkcie stałym). Oto jego zgrabny dowód (nie mój, niestety):
Jest jasne, że liczba (małych) krawędzi AB na boku dużego trójkąta jest nieparzysta (idąc wzdłuż dużej krawędzi od wierzchołka A do B musimy zmienić literę nieparzystą liczbę razy). Wędrujemy przez duży trójkąt, traktując małe trójkąty jako pokoje, a krawędzie AB jako drzwi. Każdy trójkąt ABC ma jedne drzwi, każdy inny 0 lub 2. Stąd wynika, że każda maksymalna ścieżka jest wyznaczona jednoznacznie (kiedy wchodzimy do małego trójkąta innego niż ABC, to możemy z niego wyjść tylko na jeden sposób), a jej końce są na zewnątrz dużego trójkąta, albo w jakimś małym trójkącie ABC. Wszystkie maksymalne ścieżki o obu końcach na zewnątrz dużego trójkąta „zużywają” parzystą liczbę krawędzi AB z jego brzegu, więc musi istnieć również taka ścieżka kończąca się w małym trójkącie ABC. (Tak naprawdę pokazaliśmy trochę więcej: że liczba małych trójkątów ABC jest nieparzysta).
Startujemy z dolnego boku. Mamy tam przynajmniej jeden odcinek AC.
Przeciwległy do tego boku wierzchołek nie może być B więc musi być albo A albo C. Czyli jedno z ramion tego trójkąta musi być AC. Powtarzamy ten proces aż dojdziemy do któregoś z ramion trójkąta giganta. Jeśli będzie to bok AB to wierzchołek leżący tam możemy oznaczyć tylko jako A, jeśli BC to tylko jako C. W ten sposób otrzymujemy na lewym ramieniu ciąg liter A a na prawym ciąg liter C. Na samej górze otrzymujemy więc trójkąt ABC.
Podsumowując:
Wskazaliśmy skończony ciąg operacji w wyniku których oznaczaliśmy kolejne wierzchołki: wewnętrzne jako A lub C, leżące na lewym ramieniu giganta jako A, leżące na prawym ramieniu giganta jako C.
Ponieważ proces ten zatrzymuje się przy wierzchołku B giganta otrzymujemy trójkąt o podstawie AC czego sobie nie życzyliśmy a mamy 🙂
Niedawno wpadł mi w oko filmik opowiadający zacytowany przeze mnie dowód, wraz z „praktycznym” zastosowaniem lematu: https://www.youtube.com/watch?v=7s-YM-kcKME