Jeszcze 2017
Wszystkie liczby dzielą się na dwie grupy: samorodki i rodki. Liczba S jest samorodkiem, jeśli nie ma takiej liczby, która powiększona o sumę jej cyfr byłaby równa S. Wszystkie pozostałe liczby to rodki. Od samorodków zaczynają się ciągi rodków – każda następna liczba w takim ciągu równa jest sumie poprzedniej i sumy jej cyfr. Ciągi te często się łączą, ponieważ ten sam rodek może pojawiać się w dwóch lub więcej ciągach, zaczynających się od różnych samorodków. Na przykład, samorodki 1 i 7 dają początek dwóm ciągom, które w 107 zlewają się, niczym rzeki bliźniacze, w jeden ciąg:
Liczba 2017 jest rodkiem, występującym w czterech ciągach. Dwa z nich łączą się przed 2017 w „węźle” 1918 – z tych dwóch jeden zaczyna się samorodkiem 1862:
1862→1879→1904→1918→1937→1957→1979→2005→2012→2017,
a drugi samorodkiem 1895:
1895→1918→… (dalej jak wyżej)
Trzeci ciąg dociera do ciągu będącego połączeniem dwu poprzednich w węźle 2012, a więc tuż przed 2017, a zaczyna się od najmniejszego samorodka równego 1840:
1840→1853→1870→1886→1909→1928→1948→1970→1987→2012→2017.
Czwarty ciąg zaczyna się największym z czterech samorodków, wiodących ku 2017. Jakim?
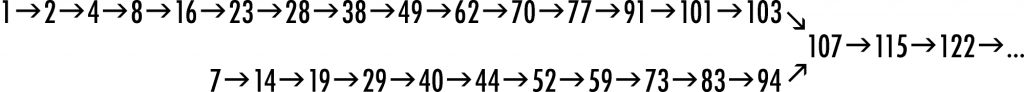

Komentarze
1952 -> 1969 -> 1994 -> 2017
Poszukiwany samorodek to 1952.
Brakujący samorodek to 1952.
1952->1969->1994->2017
1952 – 1969 – 1994 – 2017
1952 => 1969 => 1994 => 2017
Sposób rozwiązywania: wrzucamy do wora 2017 i przechodzimy do N=2016. Sprawdzamy, co urodzi N i jeśli to liczba z worka, to ją tam dorzucamy. Liczby z worka, które jeszcze nie zostały urodzone przez kolejne N, są potencjalnymi samorodkami. Pomniejszamy N o 1 i ponawiamy rodzenie i workowanie. I tak aż do momentu, gdy N będzie odpowiednio mniejsze od największego potencjalnego samorodka (wystarczy różnica 28 dla 1999 i mniejszych). W tym momencie nabieramy pewności.
I tak kolejno wrzucamy do worka:
2017
2012 => 2017
2005 => 2012
1994 => 2017
1987 => 2012
1979 => 2005
1970 => 1987
1969 => 1994
1957 => 1979
1948 => 1970
1952 => 1969
1937 => 1957
1928 => 1948
Przy 1924 stop. Ostatnie trzy liczby były podejrzane, a 1952 się przyznała.
Wychodzi na to, że jest 1952-1969-1994-2017.
1952 -> 1969 -> 1994 -> 2017
Dla tych co zrobili zadanie domowe proponuję zadanie dodatkowe 🙂
Dwóch graczy gra w Chińczyka ale DWOMA kostkami. Każdy z graczy ma dwa piony ustawione w następujący sposób:
……1XX22X1XXXXXXXXXX…..
1-pion pierwszego gracza
2-pion drugiego gracza
X-wolne pole
Gracz 2 wyrzucił właśnie 4 oczka.
Którym pionem powinien wykonać ruch gracz 2 aby gracz 1 miał mniejszą szansę zbicia któregoś z jego pionów w kolejnym swoim ruchu ?
1952
@Spytko
Jeśli się ruszy pierwszym z dwóch pionków to gracz 1 będzie mógł zbić tylko jak wyrzuci 4 albo 7 (szansa jak 9 z 36). A jak ruszy się drugim pionkiem to zbity może być przy wynikach 2, 3, 8 (szansa jak 8 z 36), czyli powinien się ruszyć drugim.
1XXX2X12XXXXXXXXX [4] [7] [1]
9 możliwości:
1+3, 3+1, 2+2, 1+6, 6+1, 2+5, 5+2, 3+4, 4+3
1XX2XX1X2XXXXXXXX [3] [8] [2]
8 możliwości:
1+2, 2+1, 2+6, 6+2, 3+5, 5+3, 4+4, 1+1
Lepiej ruszyć pionem stojącym dalej.
Jeśli dobrze zrozumiałam zadanie 🙂
Zadanie @Spytka:
Chyba to dobrze obliczyliście. Ja postanowiłem nie liczyć, tylko spontanicznie wykonać ruch tak jakbym naprawdę grał. Byłbym skłonny ruszyć pionek pierwszy, ponieważ będzie on wtedy dalej i bliżej domku. To może skompensować tę niewielką różnicę 1/36.
Wiktor10p.
Liczba 2005-2012-2017. Liczba 2005 jest samorodkiem .
@aps1968
Obliczenia czwartexa i OliGM są dobre. Pytanie dotyczyło TYLKO jednej kolejki ruchów.
Ale masz rację, całościowa strategia Chińczyka musi znajdować złoty środek między:
a) pogonią do przodu wszystkimi pionami jak najrównomierniej a
b) pozostawaniem za pionami przeciwnika w odległości dla których p-wo trafienia jest jak największe i
c) pozostawaniem przed pionami przeciwnika w odległościach dających jak najmniejsze p-wo trafienia
Myślę, że Chińczyk 2-kostkowy jest dużo ciekawszy od 1-kostkowego.
Ważną sprawą jest też dobór ilości pól planszy dla odpowiednio 2, 3, 4,….graczy.
@chińczyk
A co z dodatkowym ruchem po 6-tce lub wprowadzeniem kolejnego pionka? Trochę to zmienia bo dopuszczalne są ruchy typu: 6+4 (z wyprowadzeniem) lub znikają wszystkie dwuelementowe układy z 6-ką i pojawiają się ruch typu 5+2+1, 6+1+1 (w sytuacji dodatkowego ruchu).
@Wiktor10p
1895-1918-1937-1957-1979-2005
1862-1879-1904-1918-1937-1957-1979-2005
@Wiktor10p
Liczba 2005 nie jest samorodkiem, ponieważ 1979+1+9+7+9=2005
To ja również dorzucę zadanie z kostkami:
Należy spreparować trzy kości do gry (ozn. A, B i C), tzn. dobrać wartości na każdej z sześciu ścian tych kości, tak aby:
WIN(A,B) > 0.5
WIN(B,C) > 0.5
WIN(C,A) > 0.5,
gdzie WIN(X,Y) oznacza prawdopodobieństwo, że w jednokrotnym rzucie kośćmi X i Y na kości X wypadło więcej, niż na kości Y.
Mówiąc nieformalnie: kość A ma być lepsza od kości B, kość B lepsza od C oraz C lepsza od A.
1952-1969-1994-2017
@timon
Wydaje mi się, że jeśli rzucamy dwiema kostkami, to sprawa z powtórnym ruchem po szóstce staje się nieaktualna. Bo jak to rozumieć: że raz wypada 6? Że dwa razy wypada 6? Że w sumie wypada 6, np. 3+3? A może rzucamy najpierw i jak wypada 6 to potem jeszcze nie raz tylko 2 razy? Itd? Najprędzej chyba wariant „12”, czyli 6+6. Ale to już @Spytko ustala reguły.
@miodziu
Moja propozycja:
A => 1, 4, 4, 4, 4, 4
B => 3, 3, 3, 3, 5, 7
C => 2, 2, 2, 6, 6, 6
Żeby uniknąć sporów w przypadku wyrzucenia równej liczby oczek, rozłożyłem je tak, żeby to nie było możliwe.
Jest wiele układów spełniających warunki zadania, więc można je jeszcze doprecyzować tak: przeciwnik jako pierwszy wybiera kostkę. Dobrać wartości tak, aby zmaksymalizować szansę na wygraną (zakładając optymalną grę przeciwnika). Czyli zmaksymalizować MIN (WIN (A, B), WIN (B, C), WIN (C, A)).
U mnie ta wartość wynosi 5/9. Kto da więcej?
https://dotnetfiddle.net/Widget/ouLp30
Wiktor10p
OlaGM. Przepraszam za moje niedopatrzenie. Liczba 1952 jest samorodkiem i rozwiązaniem. Pozdrawiam.
@zadania dodatkowe
Nie wziąłem powtórnego ruchu po”szóstce” pod uwagę.
Rzeczywiście trzeba by było najpierw skonkretyzować co znaczy „wyrzucić szóstkę”. Rachunki byłyby nieco bardziej rozbudowane ale do zrobienia.
W ten sposób otwarło się szerokie pole do kombinacji 🙂 ale myślę, że na tym poprzestaniemy bo weszlibyśmy w zawiłości rachunkowe a chodziło mi tylko o zasygnalizowanie tematu 😉
Zadanie Miodzia świetne !!!
Od razu się nasuwa, że liczby na różnych kościach powinny tworzyć zbiory rozłączne bo wtedy trudniej o remisy i trudniej osiągnąć >.5
Zacząłem szukać kości 3-ściennych i bardzo łatwo ręcznie znalazłem rozwiązanie
A – 1, 5, 9
B – 2, 6, 7
C – 3, 4, 8
A wygrywa z C
C wygrywa z B
B wygrywa z A
Teraz wystarczy na każdej kości zdublować dany układ i gotowe.
Takich kombinacji jest pewnie więcej ale nie sprawdzałem komputerem.
Dla kości 2-ściennej (czyli monety) łatwo pokazać niewykonalność tego zadania.
@Miodziu
kostka A: 1,1,4,4,4,4
kostka B: 2,2,2,2,5,5
kostka C: 3,3,3,3,3,6
Przy preparowaniu trzech kości da się osiągnąć wszystkie współczynniki WIN = 21/36, np. tak:
A: 2,5,5,5,5,5
B: 1,4,4,4,7,7
C: 3,3,3,6,6,6
Zadanie można rozszerzyć na 4, 5, 6, … kostek ułożonych w cykl (sprawdzałem komputerem dla max 8 kości – rozwiązania istnieją – proponuję spróbować znaleźć jakieś ręcznie).
I kolejna wersja: przygotować 2n+1 kości tak, aby każda kość była lepsza od dokładnie n innych kości oraz gorsza od dokładnie n innych kości. Warto zauważyć, że dla n=1 otrzymujemy oryginalne zadanie 🙂
1952?
Wracając do ciągów rodków, zastanawiam się, czy byłoby tak, że każde dwa ciągi od różnych samorodków kiedyś się spotkają. A jeśli nie, to czy istnieje sposób na zidentyfikowanie na podstawie iluś tam początkowych wyrazów, że nie, te dwa na pewno się nie spotkają.
Ciekawy problem. Nie znam odpowiedzi.
mp
@aps1968
Wydaje mi się samorodek podzielny przez 9 i samorodek niepodzielny przez 9 generują ciągi, które się nie zbiegną.
Brawo Pani Olu! Istotnie, jeśli samorodek jest wielokrotnością 9, to wszystko co „rodzi” też jest podzielne przez 9. I odwrotnie – samorodek rodka podzielnego przez 9 musi być podzielny przez 9. Zatem żaden samorodek niepodzielny przez 9 nie wygeneruje rodka podzielnego przez 9.
mp
Podobnie jest dla samorodków podzielnych przez 3, a niepodzielnych przez 9 – również stanowią osobną grupę.
Eksperymentalnie sprawdziłem, że do miliona wszystkie ciągi dołączają do jednego z trzech wywodzących się od 1, 3 lub 9. Czasem są długie okresy niezależności (80219 zbiega się z 1 w 101108). Każde przekroczenie okrągłej liczby powoduje rzeź w dotychczas rozłącznych ciągach. Im bardziej okrągła granica, tym większa rzeź (100 jest bardziej okrągłe, niż 200, 1000 bardziej, niż 900).
Super! Teoria rodków w rozkwicie 🙂
mp
@OlaGM, @y-b
Dziękuję i również gratuluję. Nie ma to jak postawić dobre pytanie 🙂
Oczywiście na sytuację ma wpływ, że poruszamy się w systemie dziesiętnym. W systemie np. 9-tkowym byłoby 1-2-4-8-17-26, co się tłumaczy w dziesiętnym jako 1-2-4-8-16-24, od tego momentu dla samorodka 1 inaczej niż podano wyżej w przykładzie. Tutaj by nie działała taka cecha podzielności jak to jest w przypadku podzielności przez 9 w systemie dziesiętnym.
Ponieważ być może było to już ostatnie zadanie na liczbę 2017, chciałbym się pochwalić, że rozwiązałem problem z Omnibusa Zimowego:
1 2 3 4 5 6 7 8 9 = 2017
Trzeba wstawić po lewej stronie pomiędzy dwie cyfry jeden z czterech znaków działań, a jak nie wstawimy, to liczba się skleja, np. 45 albo 789. Pomiędzy, a więc zabroniony jest „-” przed jedynką. Oczywiście żadnych przecinków, silni, itp, żadnych nawiasów – trzeba pilnować kolejności działań.
Uściślę: Nie tyle „trzeba wstawić pomiędzy dwie cyfry”, co „można wstawić między każde dwie cyfry”, a trzeba między niektóre – tak, aby wynik się zgadzał. Byłbym zaskoczony, gdyby znalezione rozwiązanie było inne, niż podane w Omnibusie.
mp
Niestety, aż tak to nie zaskoczę 🙂