Lepsze zmiany
„Lepsze”, czyli większe niż „dobre” z poprzedniego wpisu, a ściślej – rodzaj łamigłówki taki sam, ale diagram nieco większy. To zadanie rozwiązywali uczestnicy finału łamigłówkowych mistrzostw Polski w roku 2001 i – jak wspomniałem poprzednio – wiele osób określiło je jako „irytujące”, ponieważ (zdaniem jednego z finalistów) w trakcie rozwiązywania od pewnego momentu „się głupieje”. Moim zdaniem autorowi tej lakonicznej opinii chodziło o to, że po ustaleniu kilku liczb-pewniaków, nie podlegających zmianie, logika zawodzi i trzeba wspomóc się próbowaniem i błądzeniem. Niewykluczone jednak, że komuś z Państwa uda się dostrzec jakąś ukrytą w gąszczu liter, wiodącą do celu wąską ścieżkę logiczną.
Przypominam, co jest grane:
Cyfra nad każdą kolumną i przed każdym wierszem oznacza, ile liter należy w tym rzędzie zmienić na inne. Celem zmian jest utworzenie kwadratu łacińskiego, czyli w każdym wierszu i w każdej kolumnie powinno występować osiem różnych liter – A, B, C, D, E, F, G, H.
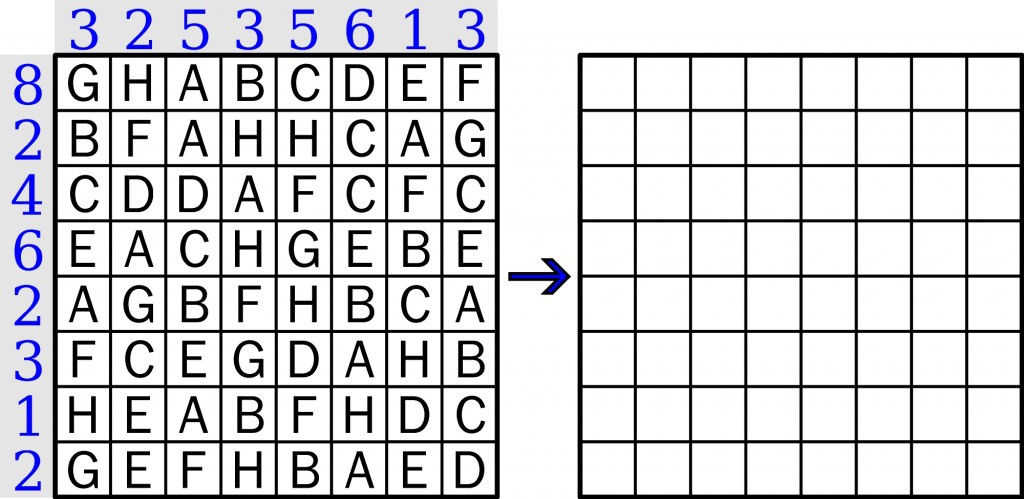

Komentarze
ABCDEFGH
BFEHDCAG
CDHAGEFB
DAGECHBF
EGBFHDCA
FCDGABHE
HEABFGDC
GHFCBAED
„Lepsza zmiana” poszła mi lepiej niż „dobra zmiana”.
Jak dla mnie zamiast wąskiej ścieżki jest szeroka szosa.
Klucz polegał na tym by znaleźć wszystkie komórki, które należy zmienić (bez świadomości na co); do tego bardzo się przydał 1. rząd (a później 4. rząd i 6. kolumna). A potem szło jak z płatka.
Rozwiązanie:
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
Mam nadzieje, ze się nie pomyliłem.
Całość poszła jak po sznurku, bez przestoju. Nie zgłupiałem :d
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
Mnie ta łamigłówka niezmiennie nie irytuje 😉 Zgłupienie też nie miało miejsca. Wręcz – podoba mi się!
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
Przypuszczam, że tamten rozwiązujący popełniał z grubsza taki błąd logiczny: „skoro jest w tym rzędzie tylko jedno B, a w każdym rzędzie musi być jakieś B, to owo B zostaje na swoim miejscu”. Potem się okazywało, że to B wypada. Stąd zgłupienie…
No, teraz było trochę trudniej. Ze dwie godziny trzeba było się zmagać. Trudniej bo większe liczby, wielkość diagramu ma dużo mniejsze znaczenie.
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
Metoda ta sama, najpierw zaznaczanie stałych liter, potem markowanie liter do zmiany, a na koniec wypełnianie. Bez jakichs specjalnych nowości, może pozatym że przy dużej ilości liter do zmiany (8 i 6) należy zacząć myśleć „odwrotnie” – ułatwia to markowanie pól do zmiany.
Jak najbardziej, da się bez żadnego strzelania, logicznie po sznurku, i zadanie nie jest wcale trudne, trzeba tylko umieć zaznaczać pewniaki do zmiany i ‚niepewniaki’:
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
Zadanie da się rozwiązać bez zgadywanek, ale na razie podam tylko końcowe rozwiązanie. Jeśli czas pozwoli napiszę więcej.
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
W pierwszym rzędzie ABCDEFGH a potem juz leci…
Doczytałem pierwszy akapit. Naprawdę irytujące? I aż z finału? To jest łatwe, acz żmudne zadanie. Rozwiązywałem w paincie. Na czerwono zaznaczałem pola, które na pewno trzeba zmienić (np. cały pierwszy wiersz) a na zielono te, które na pewno są na miejscu. Mające te dodatkowe informacje dość szybko ustala się barwę każdej litery oraz wartości kilku zmienionych liter. Mając kolor pola, zadanie sprowadza się do takiego łatwiejszego sudoku.
Też trudne nie było. Co prawda rozwiązywałem przez kilka dni, bo w czasie wolnym w pracy, ale nie strzelałem nigdzie. Początkowo zaznaczyłem litery, które muszą być zmienione, mogą być zmienione i te, które na pewno trzeba przepisać do czystego diagramu. Później operowałem na wpisanych literach już w czystym diagramie, gdzie postępowałem jak z diagramem sudoku. Wszystko poszło jak po sznureczku.
ABCDEFGH
BFEHDCAG
CDHAGBFE
DAGECHBF
EGBFHDCA
FCDGAEHB
HEABFGDC
GHFCBAED
Dzisiaj wyjaśniam obrazkowo:
http://pokazywarka.pl/lepszazmiana/
Zielone zostają na swoim miejscu, czerwone do zmiany.
Kratka po kratce zamalowujemy całą planszę bez ustalenia choćby jednej nowej literki. W tym momencie ustalenie końcowego rozwiązania jest już proste.
A B C D E F G H
B F E H D C A G
C D H A G B F E
D A G E C H B F
E G B F H D C A
F C D G A E H B
H E A B F G D C
G H F C B A E D
W żadnym momencie nie trzeba zgadywać, chyba że za zgadywanie potraktujemy metodę „nie wprost” – założenie, że w danej komórce będzie litera X i dojście do niemożności uzupełnienia innej kolumny.
Pomożecie? 🙂 Na pewno! 🙂
Chodzi o to zadanie:
http://pokazywarka.pl/yg3a6y/
Na każdym boku trójkąta ma być ciąg arytmetyczny, złożony z liczb całkowitych, dodatnich, różnych od 0.
Próbowałam ją rozwiązać metodą prób i błędów – i nic. Potem ułożyłam układ 3 równań z 3 niewiadomymi i tym sposobem znalazłam właściwe rozwiązanie. Tylko że autor twierdzi, że to jest łamigłówka… dla dzieci. A one nie znają układów równań.
Czy istnieje jakiś prosty, sprytny, łamigłówkowy, dostępny także dziecięcej wyobraźni sposób, żeby ją rozwiązać? Na co tu trzeba wpaść?
OlaGM, musisz wpaść na to, że jak wpiszesz jakąś liczbę po lewej stronie u dołu, to górna będzie o 8 większa od tej z prawej u dołu. Zatem różnica ciągu w boku z 59 wynosi 4 🙂
@OlaGM
Suma skrajnych cyfr na boku trójkąta musi być równa podwójnej liczbie środkowej.
Zatem, jeśli górna liczbę oznaczony przez x, to na dole po lewej mamy 82-x, po prawej 118-x.
Ich suma to 2*37, skąd 200-2x=74 i x=63.
@OlaGM
A teraz ten sam pomysł, ale bez równania.
Górna liczba to A, lewa dolna to B, prawa dolna to C
Różnice R1 = B – 37 oraz R2 = 37 – C muszą być równe.
Wstawiamy A=0, wtedy
B=82
C=118
R1 = 45
R2 = -81
Wstawiamy A=1, wtedy
B=81
C=117
R1 = 44
R2 = -80
Widzimy, że zwiększenie wartości A o 1 powoduje zbliżenie się do siebie wartości różnic o 2.
Zatem początkową odległość różnic (45 – (-81)) = 126 dla A=0 zniwelujemy po 126 / 2 = 63 krokach, skąd A=63
Budfy, dziękuję 🙂 Teraz rozumiem. Ogólnie rzecz biorąc, różnica między liczbami znajdującymi się w środkach dwóch boków jest różnicą ciągu na boku trzecim.
Miodziu, dziękuję 🙂 To niezłe rozumowanie, ale jak się jest biegłym w algebrze. Dziecku nieznającemu algebry nie mogę powiedzieć: „tu wstaw x, tam wstaw A i zobacz, że…”. Dzieciaki to jakoś robią bez algebry.
Pytałam kiedyś syna (9-10-letniego), jak obliczył zadanie typu ktoś ma ileś lat, inna osoba ileś więcej, a za parę lat będzie ileś razy starsza, ale nie umiał dokładnie wytłumaczyć. Powiedział, że porównuje liczby i je dobiera w głowie. Ja w takich wypadkach rzecz jasna natychmiast sięgam po algebrę.
Ta podlinkowana łamigłówka jest „9+”, a więc tylko jakieś dobieranie wchodzi w grę. Oczywiście nie zupełnie dowolne, ale ukierunkowane.
@OlaGM
Nie zgodzę się z Tobą. Algebra w moim przypadku posłużyła jedynie do zapisania myśli. Równie dobrze mógłbym zamiast
„Wstawiamy A=0, wtedy B=82, C=118, R1=45, R2=-81”
napisać
„Wpiszemy w górne pole diagramu liczbę 0. Wtedy pole na dole po lewej musi mieć 82 oraz pole na dole po prawej 118. Przy lewej części dolnego boku wpiszemy różnice pomiędzy wartością lewego dolnego pola oraz dolnego środkowego pola, czyli 45. Podobnie przy prawej części dolnego boku wpiszemy różnice między wartością dolnego środkowego pola i pola dolnego po prawej, to wychodzi -81.”
Czy oba wpisy opisują różne pomysły?
Miodziu, tak, miałeś rację. Sprawdziłam to na innym przykładzie, który również był bardzo trudny. Można to tłumaczyć na zasadzie: „wpisz dowolnie wybraną liczbę w jedno z okienek i spójrz, jak się zmieniają pozostałe”. Nie trzeba algebrą.