Po strzałkach
Od czasu epidemii sudoku kwadrat łaciński jako podstawa łamigłówek został wyeksploatowany do imentu. Opatrzył mi się, a raczej „orozwiązywał” do tego stopnia, że kiedy mam wpisywać liczby w kratki tak, aby w rzędach się nie powtarzały, to włącza się lekkie hamowanie. Do pewnego stopnia podziwiam nałogowców, którzy przynajmniej od kilku lat ślęczą w wolnych chwilach nad diagramami sudoku.
Jednak z drugiej strony od dawna poluję na oryginalne wariacje na temat łacińskokwadratowy, czyli takie, w których zgrany schemat będzie spleciony z jakimś świeżym, odkrywczym pomysłem. Jak dotąd moim faworytem jest zadanie, które nazwałem „Po strzałkach”. Autorem tego ciekawego splotu, który na pierwszy rzut oka nawet się z kwadratem łacińskim nie kojarzy, jest japoński puzzlemaster Inaba Naoki (wspominałem już o nim w jednym z poprzednich wpisów). Ale do rzeczy.
W czterech polach w każdym wierszu i w każdej kolumnie powinna znaleźć się strzałka; część pól pozostanie więc pusta. Każda strzałka w danym wierszu (kolumnie) powinna wskazywać w innym kierunku – w lewo, w prawo, w górę lub w dół.
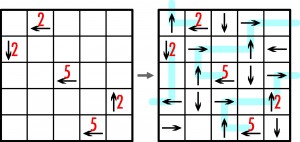
Kilka strzałek jest już na swoich miejscach, a cyfra obok każdej oznacza, ile strzałek jest w ciągu, zaczynającym się od strzałki z cyfrą. Każda kolejna strzałka w tym ciągu jest najbliższą wskazaną przez poprzednią strzałkę, a ostatnia wskazuje bezpośrednio poza diagram. W rozwiązaniu przykładu wszystkie ciągi oznaczone są jasnoniebieską linią. Poza tym, jak widać, nie wszystkie strzałki należą do ciągów.
Przykład
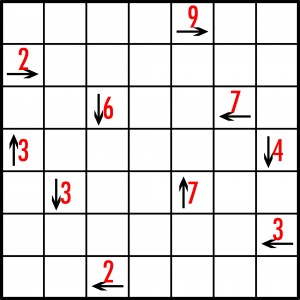
Zadanie
W rozwiązaniu wystarczy podać liczby strzałek na przekątnych, wskazujących w każdym z czterech kierunków (N-?, S-?, W-?, E-?).

Komentarze
N3 S2 W1 E1
WXXNESX
EXNSWXX
XNSXXWE
NWEXXXS
XSXWNEX
XEXXSNW
SXWEXXN
N-3, S-2, W-1, E-1
Tempus nostrum est.
Jest trochę późno, ale wydaje mi się, że… no nie wiem, pewnie popełniłem błąd, ale na rysunku czerwone strzałki to te ‚wymuszone’, zielone to te dodane ‚bo tak wypada’ i… pozostaje jedno jedyne miejsce wolne… ale niestety na drodze, na której nie powinno nic być! stawiam na 99% mój błąd, ale ten 1% zostawiam, że to jakas pomyłka w zadaniu.
Oto moja próba:
http://s30.postimg.org/iit3hf9v5/szcza_ki.png
Powinienem już uwolnić, ale jednak sporo strzałek jest w porządku, więc nie uwalniam.
mp
P.S. załóżmy, że to nie mój błąd, to mogą być 2 rozwiązania:
lewy górny róg jest 2->, i zaraz z prawej strony strzałka czerwona w górę, a nad nią w lewo, zielona. przesunac czerwona o pole w prawo a zielona o pole w lewo. Czerwona strzałka spada z przekątnej, co zmienia liczbę strzałek na przekątnych.
Liczę, że to jednak mój błąd!
Nawet nie zgadywałem 🙂
Jeśli dobrze liczę, to N-3, S-2, W-1, E-1.
{ _ _ ^ } v _
} _ ^ v { _ _
_ ^ v _ _ { }
^ { } _ _ _ v
_ v _ { ^ } _
_ } _ _ v ^ {
v _ { } _ _ ^
Pewnie się rozjedzie, więc trzeba skopiować do notatnika lub innego narzędzia XXI w. Klamerki, to strzałki w lewo, prawo. Zapewniam, że i tak jest bardziej czytelne, niż to, co sam nabazgrałem w paincie.
Dzięki za dobre słowo! Z czystego lenistwa nie drążyłem tematu, ale jak napisał mi Pan, że źle to szybciutko doszedłem do miejsca gdzie drogi wnioskowania sie rozwidlają, w tym wypadku jest to lewa górna dwójka wskazująca na prawo. W pierwszej próbie postawiłem strzałkę zaraz przy dwójce, a teraz o jedna kratke dalej:
http://s28.postimg.org/eukmu9h0d/Po_strza_kach_amiblog.jpg
Czy ciągi mogą się zlewać/schodzić/łączyć ? Nie widać zakazu w treści zadania. Może do tego prowadzić np. taki układ strzałek:prawo, dół, lewo.
Mogą. Poniewczasie doszedłem do wniosku, że lepszy byłby przykład, w którym dwa ciągi by się przecinały.
mp
lxxgpdx
pxgdlxx
xgdxxlp
glpxxxd
xdxlgpx
xpxxdgl
dxlpxxg
Odetchnąłem ! Ja też poniewczasie doszedłem do wniosku, że samo schodzenie się ciągów to jeszcze za mało i potrzebne jest ich przecinanie. Bez przecinania nie ma rozwiązania 🙂
@ Spytko z Melsztyna
A może odrobina zlewania/ schodzenia/ łączenia /krzyżowania?
______________________
|__|2v|__|__|__|__|__|__|
|__|__|__|6v|__|__|__|__|
|__|__|__|__|__|__|6v|__|
|__|__|__|__|__|__|__|3v|
|__|__|__|__|__|3v|__|__|
|8>|__|__|__|__|__|__|__|
|__|__|__|__|4>|__|__|__|
|__|__|__|3^|__|__|__|__|
Oczywiście ucieszą mnie „wrażenia” całej Społeczności, ze szczególnym uwzględnieniem Gospodarza.
Gospodarz jeszcze nie rozwiązywał, ale niebawem porozwiązuje – jak sobie ładnie narysuje 🙂
mp
Gospodarz już zmógł. Dla potwierdzenia podam, co chyba nie będzie podpowiedzią, że skrzyżowań strzałkowych ciągów jest pięć.
mp