Słupek 2016
Nie mogę się rozstać z liczbą 2016, zwłaszcza że znajomość bywa owocna. Oto ostatni owoc.
Do pustych kratek należy wpisać dziesięć różnych cyfr tak, aby powstało poprawne dodawanie liczb jedno-, dwu-, trzy- i czterocyfrowej. Temu, aby rozwiązanie było jedno, służą następujące dwa warunki dodatkowe:
– każda – oprócz jednej – para kolejnych cyfr (różniących się o 1) powinna się znaleźć w sąsiednich kratkach (stykających się bokiem lub tylko rogiem);
– żaden składnik nie może być liczbą pierwszą.
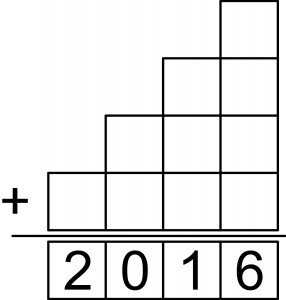

Komentarze
Rozwiązaniem może być słupek:
2
93
845
1076
Wtedy 1 i 2 są parą oddaloną od siebie, a wszystkie inne są po sąsiedzku.
Ciepło, ciepło,… ale 2 jest liczbą pierwszą
mp
OK, faktycznie zapomniałem, że 2 jest pierwsza.
Ale 1 musi być liczbą tysięcy w liczbie czterocyfrowej.
Wtedy suma liczb setek w liczbach 3 – 4 cyfrowych musi być równa 8. A żeby liczby mogły tworzyć „węża” z jedną nieciągłością, to muszą być 8 i 0.
Potem liczby dziesiątek muszą się sumować do 20, a jedności do 16.
Poprzednia wersja miała już właściwe liczby we właściwych kolumnach, ale na szczycie tę pierwszą 2.
Teraz pomieszałem je w pionie i wyszło:
6
75
843
1092
i przerwa w „wężu” też między 1 a 2.
6+75+843+1092=2016.
Świetne zadanie. Jeśli sumę cyfr tysięcy oznaczymy przez T, setek przez S, dziesiątek D a jednostek J, to oczywiście T = 1. Skoro obiema cyframi setek nie mogą być 0 i 2, wiemy na pewno, że jedną z par kolejnych cyfr niesąsiadujących będzie 1 i 0 lub 1 i 2. S może być równe 9 lub w ostateczności 8.
1) Dla S = 9, D = 9 i J = 26. S = 2+7 lub 0+9. 8 musi być cyfrą jedności, nie będzie więc na pewno graniczyć z 9 lub 7.
2) Dla S = 8, D = 20 i J = 16. S = 2+6 lub 0+8. W pierwszym przypadku cyfra 3 musi być na pozycji dziesiątek, by graniczyć z 2, a więc D = 3+9+8 (jedyna możliwość) i 5 na pozycji jedności nie graniczy z 6. Bardziej obiecujący okazuje się wariant S = 0+8. Po małej zabawie w przestawianie cyferek otrzymujemy wynik, w którym kółko się nawet zamyka (9 koło zera), a składniki nie są pierwsze choćby dlatego, że wszystkie dzielą się przez 3.
Łatwe do rozwiązania na piechotę kolumnami. W pierwszej kolumnie musi być 1, które wraz z jedynką z przeniesienia da 2. W drugiej – 8 i 0, które wraz z dwójką z przeniesienia da 10. W ostatniej kolumnie będzie zatem 2347 lub 2356, żeby sumą było 16. Ostatecznie wyszło tak:
– – – 2
– – 9 3
– 8 4 5
1 0 7 6
——–
2 0 1 6
Zapomniała Pani (nie jedyna zresztą), że 2 jest liczbą pierwszą.
mp
___6
__75
_843
1092
Na „piechotę” chyba trochę za żmudne (?)
Automatyczne Techniki Obliczeniowe też trochę muszą się nadłubać.
Jak zwykle próbuje rozwiązać zadanie w głowie. I nic mi nie wychodzi.
Do łamigłówek potrzeba kartki, ołówka i spokoju. Bez tego z reguły ani rusz.
Dodatkowo musze przyznać, że trik „wszystkie oprócz Jednego” strasznie przeszkadza. Jest to zatem dobry sposób dla autorów zadań: podać regułę, która jest prawdziwa w całym diagramie, poza jednym miejscem
… To strasznie przeszkadza 😉
Już się poprawiam 😉 Wystarczy poprzestawiać w kolumnach:
– – – 6
– – 7 5
– 8 4 3
1 0 9 2
——–
2 0 1 6
___9
__X8
_765
1234
W miejscu oznaczonym „X” miało być zero, ale przecież „zero to jest takie coś, czego nie ma” 😉
W każdym razie uznałem, że ładna, warta pokazania ciekawostka typu „o mało co”.
6+75+843+1092=2016
Jest tylko jedno rozwiązanie:
6 + 75 + 843 + 1092 = 2016
Szybko idzie rachunkiem modulo dla sum cyfr w kolumnach (pół formatu A4 obliczeń) 🙂
6 + 75 + 843 + 1092 = 2016
Jedynka musi być w kolumnie tysięcy. W kolumnie setek musi być albo 0, albo 2, bo obie na raz nie mogą być. Pozostałe wszystkie kolejne cyfry muszą być obok siebie. Stawiając na 0 obok 1 umieszczemy je na dole. Powyżej może być 8 lub 9. Wstawiając 9 okazuje się, że suma pozostałych cyfr w dwóch kolumnach jest zbyt duża (z dokładnością do przeniesienia między jednoścismi i dzięsiątkami). Pozostaje 8. Wtedy w kolumnie dziesiątek musi być 7 i 9 oraz dopełniająca do właściwej sumy 4. Teraz to już 126 sekund kombinacji, żeby właściwe cyfry były obok siebie i każdy składnik nie był pierwszą (stąd 6 będzie liczbą jednocyfrową). Dostajemy 6, 75, 843 i 1092. Ponieważ ma być jedno rozwiązanie, nie sprawdzamy już wersji z 2 obok 1 🙂