Z odpadkami
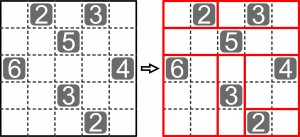
Łamiblog trochę kuleje, bo gospodarz ma sporo zajęć (dzieci, wnuki, psy, koty i takie tam podobne familijne), ale wczoraj było luźniej, więc zająłem się shikaku. Przypomnę, że to dość prosta łamigłówka z podstawowego pakietu japońskiego. Diagram należy podzielić wzdłuż przerywanych linii na prostokąty tak, aby w każdym znalazła się jedna liczba – równa liczbie kratek, tworzących ten prostokąt. Poniżej mały przykład.
Shikaku jest proste z natury. Rzec by można, nie ma siły, aby go nie rozwiązać, jakie by nie było. Właściwie jest dłubaniną dla spostrzegawczych i lekko myślących (ale nie lekkomyślnych) – zwykle trzeba tylko szukać na diagramie kolejnych pewniaków. Kusi, aby to dzierganie mniejszych i większych oczek ciut skomplikować. Przed paru laty w Łamiblogu gościły już odmiany shihaku dla nieco tęższych głów. Pora na jeszcze jedną, chyba najmniej odbiegającą od oryginału.
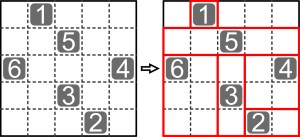
Z diagramu należy wydzielić wzdłuż linii przerywanych prostokąty – w każdym powinna się znaleźć jedna liczba równa liczbie kratek, tworzących dany prostokąt.
Przykład:
Różnica między wersją podstawową a odmianą jest więc tylko taka, że w podstawowej na prostokąty dzielony jest cały diagram, a w odmianie pozostają „odpadki” – części diagramu bez liczb.
Zapraszam do rozwiązywania odmiany.
W rozwiązaniu wystarczy podać, w ilu miejscach linie dzielące diagram krzyżują się (w przykładzie nie ma takich miejsc).


Komentarze
http://pokazywarka.pl/fd9enu/
4 ścinki, 3 skrzyżowania – o ile nie pomyliłam się w liczeniu. Trudniej wyszukać skrzyżowania i je policzyć niż rozwiązać łamigłówkę 😉
http://pokazywarka.pl/shikaku/
Obawiam się, że w tym przypadku próba skomplikowania zadania nie do końca się powiodła. Wystarczy skupić się na szóstkach i ósemce, szybko eliminuje się błędne tropy i już jest prosta ścieżka do rozwiązania.
Krzyżówek jest trzy.
Są trzy skrzyżowania.
http://pokazywarka.pl/fv0qsk/
Są trzy skrzyżowania
http://pokazywarka.pl/v8utkt/
Z poprzedniego komentarza wyżarło mi rysunek.
Są trzy takie miejsca w diagramie:
– w lewym górnym rogu pierwszej jedynki
– w prawym dolnym rogu drugiej jedynki
– w lewym dolnym rogu dwójki z przedostatniego wiersza
pozdrawiam
Suma wszystkich liczb w diagramie to 77, czyli tylko 4 pola pozostają jako odpadki.
Zaznaczyłem je na żółto-zielono.
https://drive.google.com/file/d/0Bwo1QFzne66rMnc2T29uRGktSFk/view?usp=sharing
Nie do końca rozumiem, o co chodzi z tymi krzyżującymi się liniami.
Odpowiedź to 3?
Bo mam 3 takie punkty, od których linie graniczne obszarów odchodzą we wszystkie 4 strony.
Właśnie o to chodzi – są 3 „krzyże”.
mp
Największy problem mam z poleceniem: „podać, w ilu miejscach linie się krzyżują” 🙂 Podam więc od góry rzędami od lewej do prawej, do której liczby należy dane pole, a jak do żadnej, to 0: 522084d4p43 (4d to 4 w dół, 4p w prawo, analogicznie g i l, może być też np. pg-w prawo w górę). Drugi rząd: 54d01844pg4g3. Trzeci: 54d4484103. Czwarty: 544g4lg84g044. Piąty: 54g6686644lg. Szósty: 446686634. Siódmy: 44g668663g4, Ósmy: 23338223g4. Dziewiąty: 244443334. Aby ułatwić, podam, że z trzech największych liczb, 8 jest w pionowym prostokącie 1×8 (z polem na górze, bez pola na dole), a obie 6 w prostokątach 2×3, symetrycznie, lewa w rogu lewym dolnym, prawa w prawym dolnym. Rozwiązywanie zaczęło mi się od lewej strony na dole, relacji wzajemnych 6, 3 i dolnej 4.
Linie krzyżują się 3 razy. Puste kratki: nad i po lewej kwadracika z „1” z drugiej linii oraz pod i po prawej „1” z trzeciej linii.
Linie krzyżują się w trzech miejscach.
3 skrzyżowania +
4 odpadki 1×1
http://s2.postimg.org/js8heb1nt/odpadki.jpg
Wygląda prosto.
Trzy pełne skrzyżowania:
https://app.box.com/s/9gs33jgcqmrlt0xvjqo5c7n2x6p93cz4
Pozdrawiam 🙂