Zapałek do zapałek
Korzystając z Państwa komentarzy do zapałczanego wpisu z 22 lipca, zrobiłem zapałczany rachunek sumienia, czyli coś w rodzaju erraty do rozwiązań Zapałczanek arabskich zamieszczonych w Omnibusie wakacyjnym. Uzupełniłem moje rozwiązania nadesłanymi przez komentatorów – tymi, które bez wahania można uznać za poprawne (pominąłem naciągane lub półżartobliwe). Być może ktoś z Państwa jeszcze coś doda do poniższego zestawu rozwiązań.
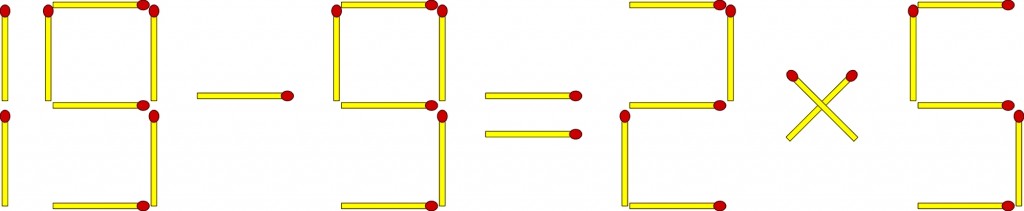
Zadanie C (równość powinna pozostać poprawna po przełożeniu dwu zapałek):
Rozwiązania są cztery (a nie trzy): 16-6=2×5, 15+3=2×9, 10-0=2×5, 18-3=3×5. I piąte: 9+9=2×9.
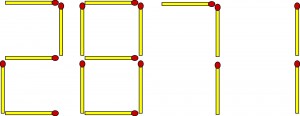
Zadanie D (liczbę należy zmienić w najmniejszą możliwą, przekładając dwie zapałki):
Rozwiązanie: 283 (a nie 2014); odpadają jako naciągane m. in. 0071 i liczby ujemne.
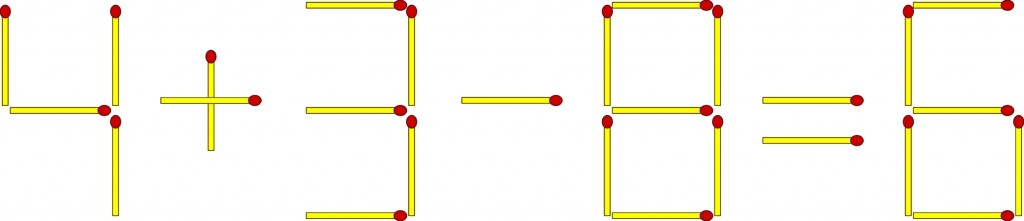
Zadanie E (do poprawnej równości prowadzi przełożenie dwóch zapałek):
Rozwiązań jest pięć (a nie dwa): 4-3+8=9, 4+2+0=6, 3+3-0=6, 9-3-0=6, 4+9-5=8.
Zadanie G (poprawna równość powstaje po przemieszczeniu dwóch zapałek):
Rozwiązania są trzy (a nie jedno): 62-59=63/21, 63+63=63×2, 62+56=59×2
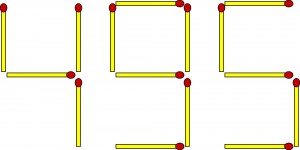
A na deser moje zapałczane zadanko z łamów amerykańskiego miesięcznika Games:
Przemieszczając dwie zapałki należy utworzyć kwadrat:
Ile jest rozwiązań?


Komentarze
484 , 1156 i 196 jedynka z ukośnym daszkiem.
Widzę dwa rozwiązania, ale pewnie jest ich z pięć…
Trzy rozwiązania: http://pokazywarka.pl/4epf9s/
W takim razie są (przynajmniej?) cztery, bo 49^2 (świetne!) było dotąd nieznane. Czwarte także jest z lekkim przymrużeniem oka.
m
W kategorii nie na poważnie też mam jedną propozycję 🙂 Ciekawe, czy to ta sama, którą Pan ma na myśli.
http://pokazywarka.pl/e9kf06/
Byłoby fajne, gdyby nie to, że konieczność przesunięcia plusa trochę „zniesmacza”. Czyli to nie to, które mam na myśli:).
mp
tylko trzy trzycyfrowe kwadraty da się ułożyć dokładnie 15 zapałkami:
225 (trzeba przełożyć 4 zapałki)
484 (trzeba przełożyć 2 zapałki)
676 (trzeba przełożyć 4 zapałki)
Czyli trzeba odrobinę poprzymrużać oko.
mp
Mam jeszcze dwa przykłady z kategorii niepoważnych, w tym jedno z niesmacznym przesunięciem, a drugie z elementem z innej czcionki:
http://pokazywarka.pl/117xsl/
196 – to jest to czwarte, które mam na myśli:)
mp
C:
9 + 9 = 2 x 9
Dopisałem (że też nikt wcześniej na to nie wpadł).
mp
po przymrużeniu oka jeszcze 1156
Dla mnie to jest bez przymrużenia. No, ewentualnie z takim malutkim 😉
mp
Cieszę się, że udało mi się znaleźć to czwarte rozwiązanie. Tymczasem mam jeszcze dwa żartobliwe: http://pokazywarka.pl/54vnzj/
Żarciki w kategorii ekstremalne 🙂
mp
a co z 11+3-8=6 ? (E)
1+13-8=6 ?
Oba są moim zdaniem „przegięte”. To z 11 powstaje po przełożeniu jednej zapałki (oczywiście, wykonując „pusty” ruch można przełożyć dwie), a w tym z 13 nie widzi mi się wciskanie 1 między + a 3.
mp
1156
po bandzie: 45/5
Widzę 2 rozwiązania w pełni spełniające założenia: 484 oraz 1156. Gdyby dopuścić „przemieszczenie” jednej zapałki poza „obszar” to można zrobić jeszcze 196. Gdyby dodatkowo spojrzeć na liczbę „do góry nogami” to z poprzednim warunkiem da się złożyć 961. Nie mogę nic wymyśleć, żeby było pięć rozwiązań, jak pisała OlaGM 🙂
Rozwiązanie najoczywistsze to 484. Rozwiązanie eleganckie to 1156. Rozwiązanie naciągane: likwidujemy dwie zapałki z czwórki tak by została jedynka i jedną z nich domykamy szóstkę, otrzymując 196. Drugą możemy skośnie dołożyć, „poprawiając” jedynkę, żeby wyglądała jak 1, a nie jak l. Albo możemy pogrubić gdziekolwiek, ale to jeszcze bardziej naciągane.
a czemu nie od razu dwa kwadraty? 🙂
49,4
49^2 (!!!)
Tak, to jest super (wcześniej wpadła na to OlaGM) i nie było mi znane.
m
484=22^2
Czyli jak na razie znamy 3 akceptowalne rozwiązania?
Jeśli w zadaniu C dopuszczałby Pan 3-elementowe jedynki, to rozwiązań byłoby więcej, np. 15-3=2×6 albo 15-9=2×3.
– 196 = (16i)^2