Pięć pierwszych
Czy pamiętają Państwo łamigłówkę KenKen? Przypomnę na mini-przykładzie na czym polega.
W pola kwadratu n×n (w tym przypadku 4×4) należy wpisać liczby od 1 do n tak, aby w każdym wierszu i w każdej kolumnie znalazły się różne liczby. Kluczem do rozwiązania jest podział kwadratu na działki złożone z kilku pól – w rogu każdej znajduje się wynik działania na wszystkich liczbach, które powinny się w tej działce pojawić. Rodzaj działania określa znak obok wyniku.
Prawdopodobnie los KenKen byłby taki, jak mnóstwa innych łamigłówek, czyli utkwiłaby ona na łamach niszowych pisemek i stron internetowych, gdyby przed sześciu laty nie przygarnął jej New York Times. A co istotniejsze, hołubi do dziś – w każdym numerze tego szacownego dziennika można znaleźć dwa zadania o różnym stopniu trudności. To prasowy ewenement. Żadne czasopismo tak wytrwale nie lansowało nowej łamigłówki.
KenKen poza rozrywkowymi ma także spore walory edukacyjne, nic więc dziwnego, że za sprawą rubryczki w NYT zaczął uatrakcyjniać lekcje arytmetyki nie tylko w amerykańskich szkołach. Przed miesiącem odbył się w Nowym Jorku pierwszy międzynarodowy turniej dla uczniów nazwany szumnie mistrzostwami świata w KenKen.
Z autorskiego, merytorycznego punktu widzenia standardowa łamigłówka ma jedną słabą stronę – nadmiar informacji. Sporo znaków działania, a niekiedy także niektóre wyniki można usunąć z diagramu, a rozwiązanie nadal będzie jedno. W ambitniejszych formach zadań ta wada bywa ograniczana lub eliminowana. Pojawiają się też mocno zakręcone odmiany KenKen. Oto jedna z nich.
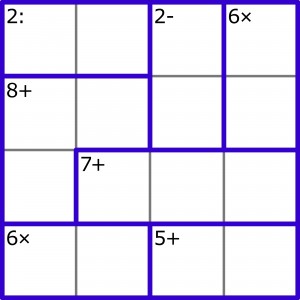
Do diagramu należy wpisać pięć różnych liczb pierwszych – oczywiście każdą pięciokrotnie i tak, aby w żadnym wierszu ani kolumnie nie było powtórek. Podane są wyniki działań, ale brak znaków określających ich rodzaje.
Czy wyniki tworzą zbiór krytyczny, tzn. czy usunięcie któregoś zwiększyłoby liczbę rozwiązań? – oto jest pytanie dodatkowe.


Komentarze
Czy nie ma błędu w tym zadaniu ? Suma liczb wiersza 4 wynosi 36 a wiersza 5 to 53. Ponieważ w obu wierszach są takie same liczby to te sumy powinny być równe. No chyba, że się mocno mylę.
Błędu nie ma. Dlaczego?
mp
Przynajmniej wiadomo, że nie ma dzielenia 😉
znak ‚-‚ oraz ‚:’ mogą znajdować się tylko w polach zawierających dokładnie dwie komórki, dobrze rozumuję?
wróć.. ‚:’ w ogóle nie może występować, wszak to liczby pierwsze…
5,17,19,2,3
19,2,5,3,17
17,19,3,5,2
2,3,17,19,5
3,5,2,17,19
Mamy jedno odejmowanie (14), dwa mnożenia (15, 18), a reszta jest dodawaniem.
Rozwiązywałem przy założeniu, że bloki trzech liczb nie mogą się opierać na odejmowaniu. Nie wiem, czy dopuszczenie np. 27=37-7-3 nie pozwoli odnaleźć innego rozwiązania. Ale to już przekracza moje dzisiejsze (i pewnie nie tylko) siły.
Początek drogi do rozwiązania:
1. 27 – wykluczamy iloczyn, bo to potęga trójki, zostaje suma. Wykluczamy z tego bloku 2, bo pozostałe pierwsze są nieparzyste i nie dadzą razem sumy nieparzystej. Gdyby wykluczyć 3, to nie uda się już zbudować sumy, więc mamy pierwszą liczbę.
2. 22 – wykluczamy iloczyn (11×2), bo jest tylko z dwóch liczb pierwszych. Możliwe tylko dwie sumy: 2+3+17 i 2+7+13.
3. 38 – wykluczamy iloczyn (19×2), j.w. Suma musi zawierać 2, bo jest parzysta.
4. Wykluczamy sumę, bo w bloku 38 jest już 2, a potrzebujemy parzystego składnika, to samo z różnicą. Zostaje iloczyn 3×5 (mamy już trzy liczby: 2, 3, 5).
5. 14 – wykluczamy iloczyn (2×7), bo dwójka jest już w bloku 22. Jedyna możliwa suma, to 3+11, ale jest jeszcze odejmowanie. W żadnej z sum 22 nie ma 5, musi być tutaj, a więc: 19-5. W takim razie blok 22 musi zawierać 3, czyli: 2+3+17. Mamy pełen zestaw liczb: 2, 3, 5, 17, 19.
Dalej już z górki.
Bo w diagramie są mnożenia i odejmowania, acz pierwszością łatwo uzasadnić brak dzieleń.
Są to następujące liczby pierwsze: 2, 3, 5, 17, 19. Liczby z działaniami: 24+, 27+, 18x, 55+, 24+, 22+,14-, 15x,38+.
5 17 19 2 3
19 2 5 3 17
17 19 3 5 2
2 3 17 19 5
3 5 2 17 19
5,17,19,2,3
19,2,5,3,17
17,19,3,5,2
2,3,17,19,5
3,5,2,17,19
Świetne zadanko Panie Marku !
Poniżej metodologia rozwiązywania krok po kroku.
1. Oczywistym jest, że w diagramie nie użyjemy dzielenia.
2. Odejmowanie może (ale nie musi) wystąpić tylko w polach składających się dwóch liczb w dolnych rzędach.
3. Chwilowo rozpatrujemy tylko trzy górne rzędy. Podane w nich liczby sumują się do 148 ale ponieważ 148 nie jest podzielne przez 3 wiadomo, że w co najmniej jednym z pól należy użyć mnożenia a nie dodawania.
4. Spośród wszystkich pięciu pól tylko 18 da się przedstawić za pomocą mnożenia. 18=2x3x3 (wpisujemy w diagram)
5. Zatem liczby pierwsze w trzech górnych rzędach sumują się do 138. 138/3=46 i tyle musi wynieść suma naszych poszukiwanych liczb pierwszych.
6. Znamy już 2 i 3. Szukamy więc trójki liczb, których suma daje 41.
Jest tylko pięć możliwości:
5+7+29
5+13+23
7+11+23
5+17+19
11+13+17
7. Liczba 55 nie może być uzyskana z żadnych trzech różnych liczb. Wiadomo więc, że jedna z liczb musi się powtórzyć. Drogą eliminacji dochodzimy do tego, że jedynie trójka 7, 17, 19 spełnia oczekiwania a 55 przedstawiamy jako sumę 19+17+19 (wpisujemy w diagram)
8. Liczba 27 wyrażona jest jednoznacznie sumą 19+5+3 (wpisujemy w diagram, kolejność również jednoznaczna)
9. Liczba 24 (po lewej) również przedstawiona jest jednoznacznie jako suma 17+5+2 (wpisujemy w diagram)
10. Liczba 24 (po prawej) podobnie jak pkt. 9
11. Przechodzimy do dwóch dolnych rzędów. 22+14 nie jest równe 46 więc 22 musi być wyrażona jako różnica lub iloczyn. Iloczynu nie da się stworzyć, zatem różnica 17-3 lub 19-5. 17-3 odpada gdyż 3 występuje już zarówno w czwartej jak i piatej kolumnie. Zatem 19-5 i kolejność wpisania do diagramu jest wymuszona.
12. Liczba 22 jest sumą 17+3+2 (wpisujemy liczby)
13. Dolny rząd uzupełniamy tak aby każda liczba występowała w każdej kolumnie.
Z diagramu na pewno można usunąć liczny z dolnego rzędu. Zdaje się, że można również usunąć liczbę 22 z rzędu czwartego.
Przypadkowo zajrzałam tu dzisiaj i widzę moje ulubione ken-ken. Miło, no to mogę się pochwalić? Rozwiązuję te łamigłówki właśnie w „NYT Magazine” – tygodniowym dodatku do codziennej gazety. Jedna wersja jest 5×5, druga 7×7. Wersja 7×7 nie jest wiele trudniejsza, gdyż liczba „7” dużo ułatwia. Natomiast w codziennej darmowej nowojorskiej gazecie AMNewYork jest każdego dnia ken ken w wersji 6×6. Łapię w tunelu metra rozdawaną gazetę i już mam zajęcie na część jazdy,
Podane w drugim diagramie wyniki działań nie tworzą zbioru krytycznego. Usunięcie trzech liczb, tj. : 24, 27 i 24 nie spowoduje utraty jednoznaczności rozwiązania.
Jaki jest zbiór krytyczny? Tego nie wiem.
Zgadzam się z Andrzejem, praktycznie wszystko rozwiązują dwa dolne wiersze i obszary z jedynymi możliwymi liczbami i ich powtórkami: 55 i 18.
Rozwiązanie
_5_17_19__ 2__3
19__2__5__3_ 17
17_19__3__5__2
_2__3_17_19__5
_3__5__2_17_19
Oprócz liczb podanych przez Andrzeja można usunąć jeszcze 38.
Mój pierwszy komentarz był bez sensu.
@Andrzej, Wiąz: zależy jak kto rozwiązuje, ja usunąłbym 3 liczby spośród 4 w dwóch dolnych rzędach 😉
W dolnym wierszu albo 15 jest iloczynem i 38 jest sumą, albo 15 jest sumą/różnicą i 38 ilorazem (zakładamy, że w użyciu są dość „małe” liczby i raczej różnica nie wchodzi w rachubę), bo występuje tylko jedna parzysta liczba pierwsza. 38 nie może być ilorazem trzech różnych liczb pierwszych, więc w diagramie występują liczby 3, 5, 2 i dwie, których suma wynosi 36. Z trzech możliwości tylko 17 i 19 pozwalają uzyskać liczby w drugim wierszu od dołu. Teraz już łatwo wpisać w diagram wszystkie liczby w następujący sposób:
5 17 19 2 3
19 2 5 3 17
17 19 3 5 2
2 3 17 19 2
3 5 2 17 19
W poprzednich komentarzach chciano usuwać liczby z dolnych wierszy. Moim zdaniem bez nich nie można odgadnąć liczb w diagramie mimo, że na pewno liczby wpisałem dopiero do poletka z liczbą 55.
5, 17, 19, 2, 3
19, 2, 5, 3, 17
17, 19, 3, 5, 2
2, 3, 17, 19, 5
3, 5, 2, 17, 19
🙂
Od góry rzędami:
5, 17, 19, 2, 3
19, 2, 5, 3, 17
17, 19, 3, 5, 2
2, 3, 17, 19, 5
3, 5, 2, 17, 19
Trochę się spóźniłem z wpisem, ale rozwiązałem wcześniej.
Zacząłem od dołu: 38 jest na pewno sumą z udziałem 2, a więc 15 może być tylko iloczynem 3 i 5. Oprócz 38, także 22 i 55 muszą być sumami, co pozwala wpaść na 17 i 19. Itd.