ABCD
W ósmym Omnibusie, z którym właśnie się uporałem i przesłałem do makietowania, będzie trochę nowych rodzajów zadań. Niektóre są mojego pomysłu, ale nie upierałbym się, że to ewidentne nowalijki, bo nie są na tyle odkrywcze, aby ktoś inny nie mógł na nie wcześniej wpaść. Niewykluczone więc, że ktoś z Państwa wskaże na przykład źródło, w którym jakiś czas temu pojawił się poniższy wariant pokropki.
Najpierw przypomnienie i objaśnienie dla nowicjuszy reguł podstawowego wariantu zabawy.
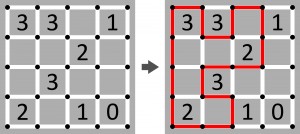
Na diagramie należy narysować linię łamaną zamkniętą, łączącą niektóre kropki i biegnącą białymi korytarzami. Kluczem do tego są cyfry umieszczone w niektórych kratkach – każda oznacza, przez ile boków danej kratki powinna przebiegać łamana. Linia nie może gościć dwukrotnie w tej samej kropce.
Przykład:
Zmiana jest niewielka: cztery różne cyfry w diagramie zastąpiono literami.
Czy teraz zadanie jest trochę czy znacznie trudniejsze?
W rozwiązaniu wystarczy podać cyfry odpowiadające poszczególnym literom.


Komentarze
trochę trudniejsze
A=3
B=0
C=1
D=2
Zamiana na literki w tym wypadku nie utrudniła zadania.
ABCD->3012
http://postimg.org/image/a0nmwygyp/
Trudno mi odpowiedzieć na pytanie, czy zadanie jest trochę czy znacznie trudniejsze, ponieważ ja zwykle nie umiem rozwiązać pokropki. Jakoś wybitnie mi to zadanie nie leży. A tę rozwiązałam, więc chyba była niezwykle łatwa…
A-3, B-0, C-1, D-2
A=3
B=0
C=1
D=2
http://oi60.tinypic.com/2yn00no.jpg
Dałem rady, więc było banalne 😉
Tak patrząc na to zadanie to nie ma znaczenia w jakim miejscu umieścimy litery i jaka będzie ich liczba. Jednoznaczność zadania i tak warunkują ujawnione liczby.
Zadanie rozwiązuje sie nie zwracając uwagi na litery. Dopiero po rozwiązaniu zadania trzeba spojrzeć gdzie są litery tylko po to, żeby podać rozwiązanie.
P.S. trzebaby mocno pokombinować w tworzeniu zadania, żeby warunek, że każda litera zastępuje inną liczbę, możnaby wykorzystać przy rozwiązywaniu.
To zadanie po usunięciu liter nadal jest jednoznaczne. Trzebaby zastąpić jakieś ujawnione liczby, które zastąpione tylko różnymi liczbami dadzą jednoznaczne rozwiązanie, a to jest chyba większe wyzwanie niż rozwiązanie jakiegokolwiek pokropka.
P.P.S. Cofam co napisałem! 🙂 ‚2’ koło ‚C’. prowadzą linie drugą stroną dwójki, koło ‚C’ dałoby rozwiązanie 3022! Wycofuję się! Warunek, że każda litera to różna liczba jest potrzebny!
A -3
B-1
C-1
D-1
Zadanie nie wydaje się trudniejszym pomimo braku czterech cyfr.
A=3; B=0; C=1; D=2;
Bez wpisania tych liczb zadanie ma 5 rozwiązań. A i D mogą mieć tylko
podane wartości. B może być równe 0 lub 1. C 1 lub 2.
A=3, B=0, C=1, D=2.
ABCD=3122
Cyfry powinny być różne.
mp
Ooops 🙁
Z tym dodatkowym warunkiem, który przeoczyłem, zadanie jest duużo łatwiejsze:
ABCD=3012
abcd = 3012
A=1
B=0
C=1
D=2
Zadanie rzeczywiście jest nieco trudniejsze.
Rozwiązanie błędne, ale nie uwalniam od razu, bo błędna jest tylko jedna cyfra (cyfry powinny być różne).
mp
Trudność zadania chyba taka sama jak przy podaniu wszystkich cyfr chociaż znając wartość A byłoby ciut łatwiej. ABCD=3012
„Czy teraz zadanie jest trochę czy znacznie trudniejsze?”
Informacja, że A,B,C i D są wzajemnie różne ustala poziom trudności zadania na właściwym, rekreacyjnym poziomie, rozwiązanie można wydedukować.
Racja, pomyliłem się:
A=3
B=0
C=1
D=2