Jeszcze dwa
Od niedawna dysponuję nowym miejscem do popełniania błędów. Chodzi o sobotni dodatek do Wyborczej „Na pamięć”, który zadebiutował pod koniec czerwca. Trochę wbrew tytułowi jest on nie tylko „lekarstwem” na pamięć, ale dotyczy wszystkiego, co może sprzyjać lepszej pracy naszych główek. Miła i urodziwa pani redaktor naczelna uznała, że powinienem uprawiać tam działkę logiczno-matematyczną, na co chętnie przystałem, a ostatnio wpadły mi jeszcze quizy.
Wracając do błędów, jak dotąd nic grubszego mi się nie przydarzyło, ale jednym mniejszego kalibru chciałbym się pochwalić.
Wśród zadań zamieszczonych 2 sierpnia znalazło się następujące:
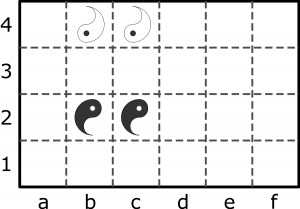
Podziel diagram wzdłuż linii przerywanych na dwie części o jednakowym kształcie i wielkości. W każdej części powinien się znaleźć jeden znak jin i jeden znak jang. Zadanie ma dwa rozwiązania. Warto spróbować znaleźć oba.
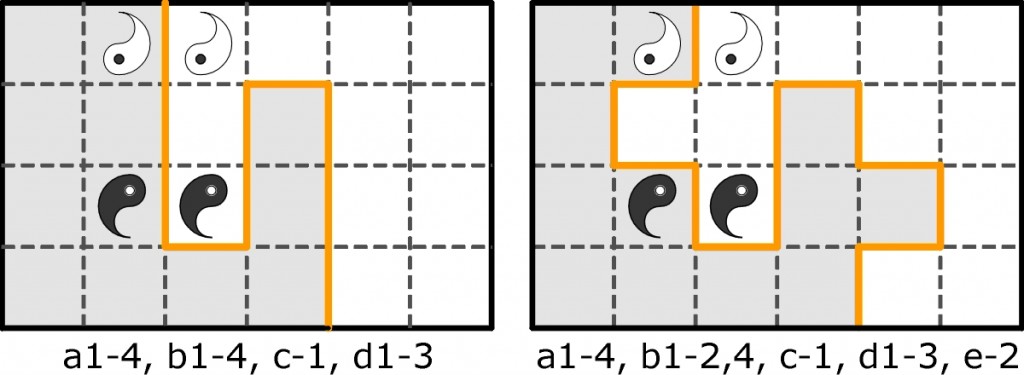
W numerze zamieszczono poniższe rozwiązania:
Tymczasem wnikliwi czytelnicy odkryli jeszcze dwa inne sposoby podziału. Proszę spróbować je znaleźć.

Komentarze
1: a1-4, b1-4, c1,3, d1,3
2: a1-4, b1,4, c1-2, d1-2, e2-3
a1-4, b1-4, c1,3, d1,3
a1-4, b1,4, c1-2, d1-2, e2-3
aabbbb
aaaabb
aabbbb
aaaabb
oraz
aabbbb
abbbab
abaaab
aaaabb
Dwa inne sposoby podziału:
ooxxxx
oxxxox
oxooox
ooooxx
ooxxxx
ooooxx
ooxxxx
ooooxx
Ja sobie to zadanie zostawiłem na potem, tzn. znalazłem jedno rozwiązanie, a nad drugim myślałem, aż tu dostałem na tacy jeszcze dwa. Moje pierwsze to było takie „kominowe”: do pierwszej części ab, do drugiej ef, i ponadto cd nieparzyste do pierwszej, parzyste do drugiej. W końcu zmobilizowałem się także do znalezienia ostatniego rozwiązania, o tyle ciekawego, że w tej samej połowie znajdują się znaki położone po przekątnej: całe a; b1,4; c1,2; d1,2; e2,3. No ale niektóre zadania z weekendowych dodatków do GW trzeba przyznać są trudne i trzeba się uciec do pomocy komputera, np. to bardzo skądinąd ciekawe z rękopisem i sumami częściowymi ciągów.
Oto pozostałe 2 rozwiązania:
XX____
XX_X__
XX_X__
XXXX__
XX____
X___X_
X_XXX_
XXXX__
Ech… przez pomyłkę wpisałem rozwiązanie podane w treści zadania 🙂
Oczywiście w zamiast niego powinno być:
XX____
XXXX__
XX____
XXXX__
a1-4, b-1,4, c3-4, d3-4. e2-3 oraz a1-4, b1-4, c-1,3, d-1,3
Zagadka ciekawa jako zadanie programistyczne. Umożliwia poćwiczenie i abstrakcyjnego myślenia, i zdolności programistycznych, i spostrzegawczości.
Warto najpierw zauważyć, że jednakowość części oznacza, że jedną figurę otrzymuje się z drugiej poprzez odbicie względem środka symetrii. A zatem problem można przeformułować jako takie oznaczenie pól zerami i jedynkami, aby odpowiadały temu figury spełniające warunki zadania.
Zatem można się ograniczyć tylko do górnej połówki – każde z 2^12 przypisań zer i jedynek do jej pól daje figury spełniające warunek przystawania do siebie. Następnie to, że każda z figur ma zawierać po jednym jinie i jednym jangu oznacza, że pola b4 i c4 oraz d3 i e3 muszą być oznaczone innymi cyframi (oznaczenie dwóch ostatnich pól poprzez symetrię od razu implikuje oznaczenie pól b2 i c2).
Samo to ogranicza ilość przypisań do przebadania do 2^10. Ponieważ zera i jedynki można zamienić miejscami, bez straty ogólności możemy zmniejszyć tę liczbę do 2^9, ustalając, że dla pola a4 przypisujemy jedynkę.
Spośród tej puli prosty algorytm odrzucający ułożenia z „samotnymi jedynkami”, a więc takimi, które nie stykają się z żadną inną, pozwala wybrać 115. A tę liczbę już bez trudu można samodzielnie przejrzeć i wybrać 4 rozwiązania, gdzie figury są „w całości”.
jedno znalezione 🙂
http://bankfotek.pl/view/1776492
jest i drugie 🙂
http://bankfotek.pl/view/1776497
Jedno rozwiazanie widać od razu: a1-4, b1-4, c1,3, d1,3.
Drugie jest nieco ciekawsze: a1-4, b1,4, c1-2, d1-2, e2-3.
Pozdrawiam.
XXOOOO
XOOOXO
XOXXXO
XXXXOO