Zerofilia
Zero jest dyskryminowane. W łamigłówkach polegających na wpisywaniu cyfr pojawia się rzadko, a często w ogóle się je wyklucza. Najlepszy przykład – sudoku. Organizacji zrzeszającej miłośników tej cyfry brak, więc protestować nie ma kto. Nie ma także Dnia Zera (bywa tylko „dzień zero”); a jest np. Dzień Liczby Pi, choć – moim zdaniem – zero jako „wynalazek” bardziej zasługuje na upamiętnienie. Szukałem w sieci zerofilów, ale trafiłem tylko na Zerofilię – komedię poniekąd science-fiction, której pikantnej fabuły z tytułu nikt by się nie domyślił. Zapewne ze względu na tę fabułę film nie był w Polsce wyświetlany.
A skoro wspomniałem o sudoku: jeszcze w roku 2004, czyli przed sudokową epidemią, japońscy zerofile i miłośnicy tej zabawy przemycili do diagramu zera – sprytnie i pomysłowo, tworząc szlachetną odmianę łamigłówki. Szlachetną, ponieważ zmienia się niewiele, rzec by można jest prawie to samo, ale „prawie robi sporą różnicę”. Potem zerowe sudoku pojawiało się od czasu do czasu na turniejach i w konkursach. Jeśli ktoś do tej pory nie miał okazji go posmakować, to nadarza się okazja.
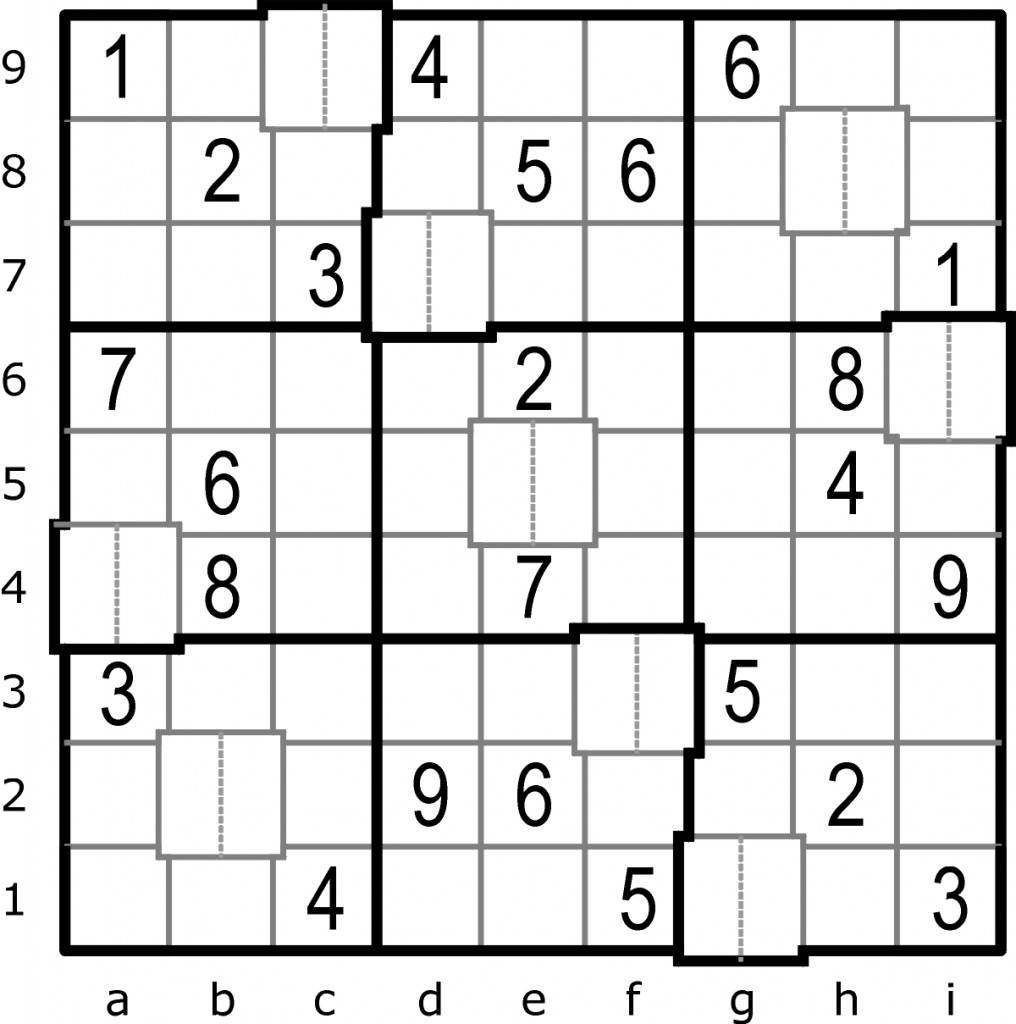
W każdym wierszu, kolumnie i sektorze obwiedzionym grubą linią powinny znaleźć się wszystkie cyfry od 0 do 9. W nieco większe pola należy wpisywać dwie cyfry.
Ogólnie rzecz biorąc, sudoku z zerami jest nieco trudniejsze od zwykłego. Nie wszystkie tradycyjne sposoby rozwiązywania działają, choć początek rozwiązywania bywa podobny. Potem trzeba bardziej uważać i pamiętać o zerze.
W rozwiązaniu – gdyby ktoś zechciał się podzielić sukcesem – wystarczy podać współrzędne pól z zerem solo.

Komentarze
a5, b9, c2, d3, e7, f4, g1, h8, i6
Moim zdaniem zadanie ma dwa rozwiązania, niewiele się od siebie różniące. W obu zero występuje na polach e7, a5, f4 i d3, a w jednym dodatkowo b9 i c2 (wymiennie z cyfrą 5)
a5, b9, c2, d3, e7, f4
lub
a5, d3, e7, f4
10(57)438692
9281563(07)4
643(27)09851
73952418(06)
0623(89)1745
(45)81670239
39604(27)518
8(15)0963427
274815(09)63
albo
15(07)438692
9281563(07)4
643(27)09851
73952418(06)
0623(89)1745
(45)81670239
39604(27)518
8(01)5963427
274815(09)63
Znalazłem dwa rozwiązania, w których zera solo znajdują się w następujących polach:
Rozw. 1.: 3d, 4f, 5a, 7e.
Rozw. 2.: 2c, 3d, 4f, 5a, 7e, 9b.
Próbowałem na piechotę i nic nie wychodziło (zbyt mało czasu). Po napisaniu programu odkryłem, że łamigłówka nie jest jednoznaczna… Wszystkie układy umieszczam tutaj: http://www.gg.pl/dysk/zjFuyn3TmN1QzzFuyn3TiPQ/out.txt
W przyjętej notacji zapisuję tylko po jednej wartości dla pól powiększonych – druga wartość to ta, która nie występuje w danym wierszu/kolumnie/kwadracie
Zaciekawił mnie fakt, że rozwiązań jest dokładnie 1024 = 2^10 – może wszystkie te diagramy są takie same z dokładnością do kilku pól, w których można na 2 różne sposoby dokonać wyboru?
Ostatnio lubię się chwalić, więc pochwalę się ponownie. Tym razem w formie zagadki, kto zgadnie proszę nie ujawniać rozwiązania, w razie czego rzucę podpowiedź a rozwiązanie w komentarzach do następnego wpisu na blogu 🙂
++++++++++++++++[>+++>++>++++++>+++++++<<<+++.–.>.>>—.+++++.<++.–.>+++.—.—.+++++++++++.<+++++.+++.+.—-.>——-.<.—-.>.++++++.———–.<<.>——————.>++++++.-.—-.<<.>++.—-.++.<.>——.>–.<<+.
Nie no… znowu forum zmodyfikowało treść mojego komentarza :/
Wklejam jeszcze raz, licząc na poprawne wyświetlenie:
++++++++++++++++[>+++>++>++++++>+++++++<<<+++.–.>.>>—.+++++.<++.–.>+++.—.—.+++++++++++.<+++++.+++.+.—-.>——-.<.—-.>.++++++.———–.<<.>——————.>++++++.-.—-.<<.>++.—-.++.<.>——.>–.<<+.
Skoro forum nie współpracuje, to zagadkę umieszczam tutaj: http://www.gg.pl/dysk/YLmtFN3_G-5QYbmtFN3_C8c/zagadka.txt
Czy zagadka ma dwa rozwiązania?
a5, b9, c2, d3, e7, f4 lub a5, d3, e7, f4
Rozwiązałem diagram i na końcu do wpisania zostało mi dwa razy 5 i dwa razy 0 przy wolnych polach b2, b9 oraz c2, c9. Błędu nie znalazłem.
Tak, dwa.
mp
Solowe zera są na polach : e7 , a5 , f4 , d3 oraz (b9 albo c2) .
A ponieważ „zero solo” to brzmi prawie jak „Han Solo” , to zadanie jak najbardziej na czasie 🙂
Pozdrawiam
AC
Albo czegoś nie widzę, albo jest w tym rozpulchnionym sudoku prawdą, że mogą być dwa rozwiązania: 0 i 5 w wierszach 2. i 9., kolumny b i c, znaczy jak 0 w b2 i c9, to 5 w c2 i b9, i odwrotnie. Pozostałe pola z singlowym zerem to d3, f4, e7 i a5. Być może po dodaniu zera taka podwójność musi mieć miejsce. Rozwiązywało się właściwie jak normalne sudoku.
Rozwiązanie są dwa:
2c;3d;4f;5a;7e;9b
3d;5a;4f;7e;
W wierszach 2 i 9 można zamienić miejscami 0 i 5.
1,0,(7,5),4,3,8,6,9,2
9,2,8,1,5,6,3,(0,7),4
6,4,3,(2,7),0,9,8,5,1
7,3,9,5,2,4,1,8,(6,0)
0,6,2,3,(8,9),1,7,4,5
(5,4),8,1,6,7,0,2,3,9
3,9,6,0,4,(2,7),5,1,8
8,(1,5),0,9,6,3,4,2,7
2,7,4,8,1,5,(0,9),6,3
Drugie
1,5,(7,0),4,3,8,6,9,2
9,2,8,1,5,6,3,(0,7),4
6,4,3,(2,7),0,9,8,5,1
7,3,9,5,2,4,1,8,(6,0)
0,6,2,3,(8,9),1,7,4,5
(5,4),8,1,6,7,0,2,3,9
3,9,6,0,4,(2,7),5,1,8
8,(1,0),5,9,6,3,4,2,7
2,7,4,8,1,5,(0,9),6,3
nie wiem dlaczego, ale tak niefajnie wychodzą mi 2 rozwiązania: poza zerami w e7 a5 f4 d3 mamy do wyboru: b9 lub c2
@miodziu
Gratulacje! 🙂