W Math-Pays
Jeden ze stałych gości Łamibloga zwrócił moją uwagę na dość trudne zadanie zamieszczone w tegorocznym zestawie eliminacyjnym do Mistrzostw w Grach Matematycznych i Logicznych. Eliminacje zakończyły się w styczniu (zestaw jest nadal do pobrania na stronie mistrzostw), więc z czystym sumieniem można się zająć wspomnianym zadaniem – ciekawym i oryginalnym.
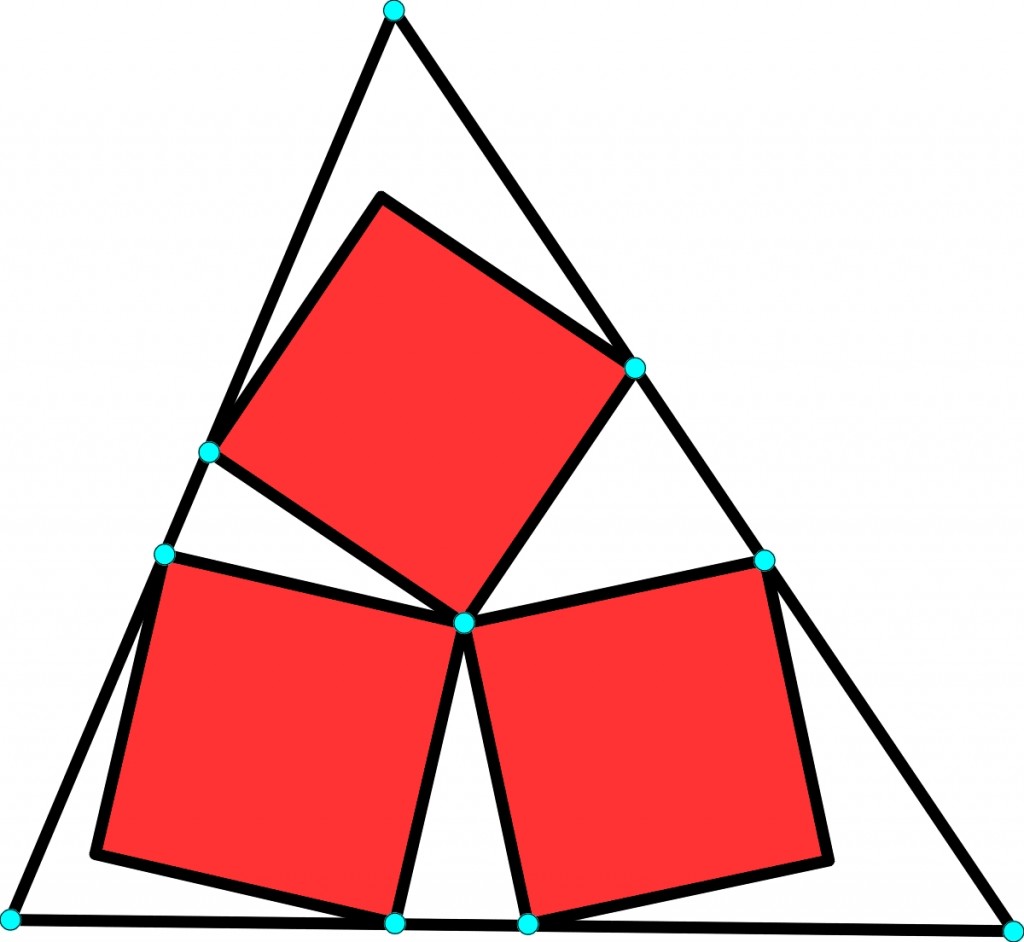
Znak drogowy w Math-Pays, sygnalizujący spadanie kamieni ze zboczy, ma kształt trójkąta. Trzy kolorowe kwadraty nie zachodzą na siebie, mają wspólny wierzchołek i każdy z nich ma dwa wierzchołki na boku trójkąta. Bok każdego z trzech kwadratów ma długość 2,8 decymetra. Kąt trójkąta, przeciwległy do boku o długości 10,8 decymetra ma 75 stopni. Jakie jest, w cm2, pole trójkąta? Figura na rysunku nie przedstawia dokładnie ani kątów ani proporcji.
Konkretne rozwiązanie jest znane – 3749 cm2, chodzi natomiast o podanie wzoru ogólnego na S (pole trójkąta) w zależności od długości a (boku kwadratu) i b (boku trójkąta leżącego naprzeciw kąta równego 75 stopni).
Ani sam wzór, ani znalezienie go nie jest proste.

Komentarze
No to sie pochwalę: byłem kiedyś Mistrzem Polski w Grach Matematycznych i Logicznych.
Potem przestałem w tym startować, bo coraz częściej zadania były nieprecyzyjnie sformułowane i osobiście kilka razy straciłem przez to ważne punkty. Może ostatnio coś się zmieniło na lepsze? Warto zobaczyć…
Niech p = sqrt(3).
Wtedy wysokość trójkąta h opuszczona na bok o długości b wyraża się wzorem h = ab(1+p) / (2b – 2ap)
Wtedy pole trójkąta to oczywiście P = bh/2 = ab^2(1+p) / (4b-4ap)
Po podstawieniu a=28cm, b=108cm wychodzi P=3748.85415268, co po zaokrągleniu zgadzałoby się z podaną wartością 3749.
Panie Marku, proszę o potwierdzenie wzoru. Jeśli będzie ok, postaram się przygotować poglądowy opis uzyskania wzoru.
Potwierdzam – jest OK.
mp
Poniższy opis jest poglądowy, mam nadzieję, że zainteresowani zrozumieją moje intencje.
Rysunek do opisu znajduje się tu: http://www.gg.pl/dysk/F1L57yFIKV9QFlL57yFIOXY/rys.jpg
Przyjmujemy p=sqrt(3)
Na rysunku zostały oznaczone punkty, punkt wspólny kwadratów to J (słabo widać na rysunku). Dodatkowo zakładamy, że miarę 75 stopni posiada górny kąt trójkąta ABC, czyli ten przy wierzchołku A.
Punkt K jest środkiem odcinka DE, L środkiem FG, M środkiem HI. Ponieważ trójkąt DEJ jest równoramienny (równość boków JD i JE), zatem punkt K jest również spodkiem wysokości tego trójkąta opuszczonej z punktu J. Wiemy zatem, że prosta JK jest prostopadła do prostej AC.
Na rysunku zaznaczono również kąty DJK oraz EJK – w związku z powyższym miary obu kątów są równe, a ich miarę oznaczam jako x (również zaznaczone na rysunku)
Analogicznie mamy dla punktów L i M. Na rysunku oznaczono miary kątów FJL i GJL jako y oraz miary kątów HJM i IJM jako z.
Teraz nieco obliczeń: kąt pełny przy punkcie J ma miarę 360 stopni. W jego skład wchodzą 3 kąty proste zawarte w kwadratach oraz 2(x+y+z). Stąd mamy 2(x+y+z) = 360 – 3*90 = 90, czyli x+y+z=45.
Suma kątów czworokąta AKJM wynosi 360, a składają się na nią: kąt A trójkąta ABC, dwa kąty proste przy wierzchołkach M i K oraz kąt przy wierzchołku J o mierze x+z+90. Zatem 360 = 75+90+90+x+z+90, czyli x+z=15.
Skoro x+y+z=45 oraz x+z=15, to y=30, a to oznacza, że trójkąt GFJ jest równoboczny (nie widać tego na rysunku).
Dalej zauważamy, że punkty E i H znajdują się na tej samej wysokości (w stosunku do podstawy BC). Dodatkowo możemy wyliczyć tę wysokość, jest ona sumą wysokości wysokości trójkąta JFG (ap/2) oraz wysokości punktu H ponad punkt J. Ta ostatnia ma wartość a/2 (bowiem prosta HJ jest pochylona o 30 stopni w stosunku do BC).
Również łatwo możemy wyliczyć długość odcinka EH, jest on bowiem podwójną wysokością trójkąta równobocznego o boku a, czyli EH=ap
Teraz korzystamy z podobieństwa trójkątów ABC oraz AHE.
Wysokość trójkąta ABC to h, natomiast wysokość trójkąta AHE to h-(wysokość punktu H ponad prostą BC), czyli h-ap/2-a/2.
Korzystamy z proporcji h/b = (h-ap/2-a/2)/(ap), z której mamy
hap = (h-ap/2-a/2)b
2hap = (2h-ap-a)b
2hb – 2hap = apb+ab
h(2b-2ap) = ab(1+p)
h = ab(1+p) / (2b-2ap)
Ostatecznie, pole ABC to P = hb/2 = ab^2(1+p) / (4b-4ap)
Głowię się nad tym drugi wieczór… Panie Marku, czy nie pominął Pan jakiejś informacji potrzebnej do uzyskania rozwiązania?
Nie, niczego nie brakuje. Zadanie jest po prostu trudne, może nawet bardzo. U nas w eliminacjach rozwiązało je 27 osób, ale np. w Belgii nie rozwiązał go nikt.
mp
Mam wrażenie, że w poprzednim wpisie słabo opisałem liczenie odległości punktów H i E od prostej BC.
Umieszczam kolejny rysunek, w którym starałem się zachować rzeczywiste wartości kątów: http://www.gg.pl/dysk/I9IQZAEF58JQItIQZAEF9-s/rys2.jpg
Odległość punktu H od prostej BC z poprzednich obliczeń to a/2 + ap/2. Z rysunku widać, że ta odległość to po prostu długość odcinka OL, będąca sumą długości OJ i JL. OJ = a/2 (jako połowa boku trójkąta równobocznego o boku długości a, bowiem trójkąt HOJ jest połową trójkąta równobocznego) oraz JL = ap/2, bo jest po prostu wysokością trójkąta równobocznego o boku a.
Mam nadzieję, że teraz wszystko jest jasne.
Jak takie trudne, to sugerowałbym jeszcze dzisiaj nie uwalniać 😉 jestem chyba na tropie, ale dwa wieczory Rubika to może być za mało. Zresztą najwyżej jak zostanie uwolnione, to nie będę patrzył. Tak się robią zaległości na Łamiblogu…
Na razie rozwiązanie nadesłała jedna osoba. Uwolnię, jak się pojawi drugie rozwiązanie, czyli najwcześniej jutro (piątek).
mp
Chyba zabrnąłem za daleko, kończy się to pochodnymi, stycznymi i tw. cosinusów… Chyba, że w złą stronę poszedłem i można prościej.
Pochodne to rzeczywiście nie tędy droga.
mp
A co sądzicie o wprowadzeniu rankingu czytelników? Za każde rozwiązanie można by dostać punkt lub kilka puntków, jeśli zadanie jest trudniejsze. Ewentualnie można rozważyć punkty cząstkowe za częściowo poprawne rozwiązanie (np. gdy rozwiąże się jeden z kilku przykładów). A na koniec miesiąca podsumowanie i zwycięzca z zaszczytnym tytułem Łamigłowy miesiąca.
Miodziu, sorry, ale z różnych względów ten pomysł mi się nie widzi i nie sądzę, aby wypalił. M. in. ze względu na skromne grono rozwiązujących i komentujących oraz różne rodzaje zadań. Poza tym wolę luz niż rywalizację.
mp
Trzeba jakoś skonstruować funkcję zależną od wartości kąta pomiędzy poziomą podstawą trójkąta a bokiem lewego dolnego kwadratu. Kąt przyjmuje wartości (0 st ; 15 st) i przy wartościach granicznych długość boku b przyjmuje wartości minimalne (równe sobie, mniejsze od 108 cm). Zatem wykres długości boku zależny od kąta będzie miał postać jakiejś paraboloidy z ekstremum większym od 108. Istnieją zatem dwa możliwe kąty dla których bok b będzie miał długość 108. Zatem najpierw trzeba ustalić wzór tej funkcji a następnie dojść jeszcze do pola trójkąta. Kosmos jakiś. Poddaję się 🙁
Bez żalu poddałem się. Narysowałem sobie koło „opisujące” kwadraty i „wpisane” w trójkąt. Sparametryzowałem wszystko w układzie współrzędnych o środku w punkcie łączenia kwadratów. Skorzystałem z 75st. I wszystko wygląda w miarę znośnie aż do momentu kiedy liczę odległość między punktami, bo ten wzór wygląda parszywie… na pewno się upraszcza, ale mi się jednak już chyba nie chce.
Na liczbach to jeszcze nawet wychodzi, ale nie chce mi się przekształcać wzorów.
Zadanie jest stosunkowo proste, jeśli ma się rozszerzoną wiedzę na temat trójkątów. Jeżeli znacie i wiecie, co to jest okrąg 9-ciu punktów, to rozwiązanie jest widoczne od razu. Wychodzi się od sposobu wpisywania trzech kwadratów w trójkąt.
1. Kreślimy symetralne boków, aby znaleźć środek i promień okręgu opisanego na trójkącie nazwijmy go O.
2. Znajdujemy punkt przecięcia się wszystkich wysokości trójkąta. Ten punkt nazywa się ortocentrum P.
3. Dzielimy odcinek P O na połowę i oznaczamy ten punkt N. Punkt N jest środkiem okręgu 9-ciu punktów. Promień okręgu 9-ciu punktów jest równy połowie promienia okręgu opisanego na trójkącie. Okrąg 9-ciu punktów przecina każdy bok trójkąta w dwu punktach:
a.) Jeden punkt to środek każdego z boków trójkąta;
b.) Drugi, to jest spadek wysokości trójkąta na każdy bok.
4. Opisane powyżej punkty są tymi punktami na rysunku z zadania, gdzie kwadraty stykają się z bokami.
5. Środek okręgu 9-ciu punktów N, to punkt wspólny trzech kwadratów.
Wszystko to można znaleźć w Wikipedii pod hasłem: Okrąg 9-ciu punktów. Warto również przeczytać w Wiki tekst pod hasłem geometria trójkąta.
To są wszystkie wskazówki potrzebne do rozwiązania tego zadania.
Grace w imieniu Wiktora.
P=(b^2*x*a*sqrt(2)*sin(75)*0,5)/(x^2-2*sqrt(2)*a*cos(75)*x+2*a^2)
gdzie:
x=(b-a(-/+)sqrt(delta))/2 (obojętne czy weźmiemy plus czy minus pierwiastek z delty, wynik będzie ten sam)
delta=(b-a)^2-(2*sqrt(2)*a)^2
Prowadząc rozwiązanie trochę inną ścieżką od pewnego momentu otrzymamy inny wzór o podobnym stopniu złożoności:
P=((b^2*x)/(2*sqrt(2)*a*sin(75)))*(B^2/(A^2+B^2))
gdzie:
x=jak wyżej
A=x-a*sqrt(2)*cos(75)
B=a*sqrt(2)*sin(75)
Kluczem do rozwiązania było spostrzeżenie, że wewnątrz trójkąta wyjściowego można dostrzec trójkąty podobne do niego i siebie nawzajem. W podanym wyżej pierwszym wzorze pracuje też tw. cosinusów a w drugim wzór na sinus sumy kątów.
A jednak można! Skoro a jest bokiem kwadratu, niech trójkąt ma boki b, c i d.
1. Z rachowania kątów wynika, że trójkąt „naprzeciwko” wierzchołka 75° (z wierzchołkiem w punkcie styku 3 kwadratów i bokiem zawartym w b) jest równoboczny, oczywiście o boku a. Niech jego wierzchołki dzielą zatem bok b na odcinki b1, a i b2.
2. Teraz zwróćmy uwagę na trójkąty: b1-przekątna kwadratu-trzeci bok zawarty w d, oraz b2-przekątna kwadratu-trzeci bok zawarty w c. Znów z rachowania kątów wyjdzie nam, że kąt między b1(b2) a przekątną (o długości asqrt2) jest 75° (część „biała” 30, część „czerwona” 45). Skoro trójkąt duży i każdy z tych dwóch mają po 2 kąty równe (jeden wspólny, a drugi 75), to są to trójkąty podobne. Trzeba się przypatrzyć, by wskazać odpowiadające sobie boki i ułożyć proporcję, w każdym razie będziemy mieć: b1/asqrt2 = d/c i b2/asqrt2 = c/d. Stąd b1*b2 = 2*a*a. Natomiast b1 + b2 = b – a. Stąd obliczamy b1 i b2 w funkcji a i b, będą to pierwiastki równania kwadratowego.
3. Mamy teraz obliczony stosunek d/c (i oczywiście c/d). W dużym trójkącie znamy kąt, bok naprzeciw niego i stosunek dwóch pozostałych boków, co pozwala nam rozwiązać ten trójkąt. Na przykład tak: na ramionach kąta 75° odkładamy boki 1 i (c/d) i znajdujemy trzeci bok x takiego małego trójkąta z twierdzenia cosinusów: x^2 = 1 + (c/d)^2 – 2*(c/d)*cos 75. Teraz wystarczy obliczyć x, skalą podobieństwa będzie b/x, i przez b/x pomnożyć boki 1 i (c/d). W ten sposób obliczymy boki c i d.
4. W ostatnim kroku obliczamy pole trójkąta jako c*d*(sin 75)/2. I tu jest właśnie problem, bo w zadaniu polecenie jest, by podać wzór, i ja pozwolę sobie zaproponować taki prosty wzór, i zauważyć, że wartości c i d otrzymujemy w wyniku procedury z punktów 1-3 😉 jako dość skomplikowane, ale jednak funkcje tylko a i b. Dałoby się to odtworzyć z moich obliczeń dla podanych wartości a i b w kilkunastu komórkach excela, w każdym razie wynik wychodzi dobry, co pozwala mi uznać zadanie za rozwiązane i rozważyć, czy złożyć wniosek o przyznanie obywatelstwa belgijskiego 🙂 .
U nas w mieście są dwa licea „matematyczne”. W moim się opowiadało taki dowcip: zadano uczniom nauczenie się na pamięć książki telefonicznej. Uczniowie ze szkoły konkurencyjnej spytali na kiedy, a z mojej – po co? Więc pytam się, po co robić zadanie nie mającego eleganckiego rozwiązania? Jak w ogóle zapisać
rozwiązanie w niewielkim okienku tekstowym tego bloga?
Zakładając, że istnieje wyłącznie żmudne rozwiązanie, można je znaleźć siłowo w następujący sposób:
1. jeden z białych trójkątów na rysunku powyżej jest równoboczny (ten naprzeciwko kąta 75),
co wynika z miary 75 stopni, równoramienności białych trójkątów, sum kątów w trójkącie i czworokącie etc.
2. jeżeli poprowadzimy prostą przez przekątną dowolnego kwadratu przechodzącą przez 2
punkty leżące na trójkącie, to ta prosta odetnie z trójkąta trójkąt do niego podobny o jednym boku
mającym znaną długość a*sqrt(2), co pozwala wyrazić długości jego pozostałych boków jako proste
funkcje długości boków trójkąta i boku kwadratu.
3. Z a i b) można ułożyć równanie na długość boku leżącego naprzeciwko kąta 75 (czyli na b).
4. To jest równanie kwadratowe na iloraz c/d długości boków trójkąta przy kącie 75
o jednym pierwiastku dodatnim i 1 ujemnym; wybieramy ten dodatni, ale wzór już jest nieprzyjemny.
5. Mamy więc trójkąt o danym kącie 75, długości naprzeciwległego boku b i ilorazie długości
pozostałych boków c/d. Zadanie jest już rozwiązywalne, choć wzory nie są proste.
6. Z uogólnionego Pitagorasa piszemy wzór na b^2 i wykorzystujemy to, że znamy c/d.
Stąd można wyznaczyć długość każdego boku jako funkcję a,b i cosinusa 75.
(cos(45+30)=(sqrt(6)- sqrt(2))/4 ), podobnie z sinusem 75.
7. Mając długości 3 boków, pole otrzymujemy z Herona albo znanego wzoru z sinusem kąta 75.
8. To jest na tyle żmudna droga, że pozwolę sobie poprzestać na jej wskazaniu, za szczegóły mogą się wziąć
młodsi, zwłaszcza ci z konkurencyjnego liceum.
Echh sądziłem, że w zadaniu jest jakiś haczyk a tu proszę 🙂 czysta matematyka, wystarczyło dojść do tego, że jeden z trójkątów jest równoboczny, dalej idzie z górki,
@miodziu: dziękuję za doskonałe przedstawienie jak dojść do rozwiązania.
Mistrzostwo Polski widać nie poszło na marne 🙂
Gratulacje dla Miodzia,
Jak już się okazało, że rozwiązanie jest elementarne a końcowy wzór prosty, wziąłem kartkę papieru i przeliczyłem zadanie moją metodą, obyło się bez wyliczania delt i pierwiastków dwóch równań kwadratowych, które czyhały po drodze, wszystko się ładnie skróciło dokładnie do wzoru Miodzia.
Czy w tych zawodach Math-Pays czas był ograniczony, czy też zadania można było robić w domu?
Pierwszy etap eliminacji był domowy i trwał parę miesięcy.
mp
Zgłaszam się po terminie, bo z czasem u mnie było krucho, ale że zadanie było fajne, więc na tyle go wyskrobałam, by rozwiązać. Gratuluję Miodziu, wynik otrzymałam identyczny, ale rozwiązanie nie tak eleganckie – po prostu nie przyuważyłam podobieństwa trójkątów. Poszłam więc na łatwiznę.
Cały trójkąt umieściłam w układzie kartezjańskim, gdzie bok przeciwległy kątowi 75 st. leżał na osi OX, oś Y przecinała ją w połowie boku trójkąta równobocznego. Że równoboczny, to jasne. Potem już wystarczyło napisać odpowiednie równania boków, znaleźć punkt ich przecięcia, którego współrzędna y-kowa to szukane h. Ale!
By napisać owe równania potrzebowałam współrzędnych wierzchołków trójkąta , tych leżących na osi OX – wprowadziłam więc parametr s i wtedy A(s,0), B(s+b,0). Gdy znalazłam wierzchołek C[ap(2s+b)/(2ap-2b);ab(1+p)/ (2ap-2b)] – p to p Miodzia, zaś a to bok kwadratu – i okazało się, że trójkątów jest nieskończenie wiele – s może przyjmować wartości z pewnego przedziału, natomiast wysokość jest taka sama dla wszystkich. Oczywiste jest, że trójkąty różnią się między sobą kątem przy wierzchołku C, ale jednym z nich jest nasz kąt 75 st. I odpowiadający mu wierzchołek też ma taką samą współrzędną y-kową, a trójkąt taką samą wysokość jak pozostałe – h = ab(1+p)/(2b-2ap). Ponieważ należało znaleźć pole,nie zaś konkretne wierzchołki,więc można się nie przejmować szukaniem właściwego s, tylko obliczyć S = b*h/2
Pozdrawiam
Anka