Dürer antymagiczny
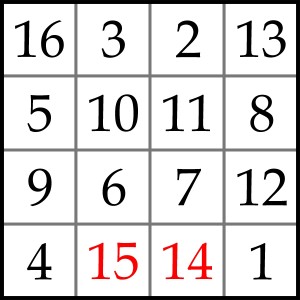
W prawym górnym rogu słynnego miedziorytu Albrechta Dürera Melancholia, znajduje się niezwykły kwadrat magiczny 4×4:
Krój cyfr jest staroświecki i nie wszystkie są wyraźne (widać np., że w pierwszym polu drugiego rzędu mistrz się kropnął i najpierw wyrył szóstkę, którą później poprawił na osobliwie wyglądającą piątkę), więc gwoli jasności obok zamieściłem elegancki współczesny monitoryt.
Kwadrat Dürera zwany jest czasem supermagicznym, bo magii jest w nim aż nadto. Sumę magiczną (34) tworzą nie tylko czwórki liczb w rzędach, kolumnach i na przekątnych, ale także znajdujące się w wielu innych regularnie rozmieszczonych kwartetach pól – na przykład w tworzących narożne i środkowy kwadraty 2×2; poza tym sumę 34 daje każda para par liczb umieszczonych symetrycznie względem środka.
W grudniowym Świecie Nauki było zadanie pozakonkursowe (trudne i żmudne), którym teraz postanowiłem poczęstować gości Łamibloga z wątłą nadzieją, że ktoś się na nie połakomi. Mówiąc krótko, chodzi o przerobienie supermagicznego kwadratu Dürera, na kwadrat antymagiczny. A nieco dłużej: należy przestawić jak najmniej cyfr liczb, czyli siedem – tak, aby wszystkie dziesięć sum (w rzędach, kolumnach i na przekątnych) było różnych i w dodatku aby sumy te tworzyły fragment ciągu liczb naturalnych. Ale to nie wszystko, bowiem Dürer zażyczył sobie także, by 15 i 14, tworzące rok powstania dzieła, były wśród dziewięciu, które pozostaną na swoich miejscach. Powstanie więc kwadrat antymagiczny Dürera.
Zadanie jest karkołomne nawet dla komputera; podejrzewam, że będzie pierwszym (jeśli mnie pamięć nie myli), którego nikt nie rozwiąże.


Komentarze
Nie do końca rozumiem zdanie: ” aby wszystkie dziesięć sum (w rzędach, kolumnach i na przekątnych) było różnych i w dodatku aby sumy te tworzyły fragment ciągu liczb naturalnych.”
(a) Czy chodzi o to, aby było to dziesięć kolejnych liczb naturalnych w dowolnej kolejności?
(b) Czy może chodzi o to, aby kolejno sumy w rzędach, potem kolumnach i na końcu przekątnych, tworzyły fragment ciągu liczb naturalnych?
Chodzi o (a); podejrzewam, że (b) jest nie do zrealizowania.
mp
Jeśli na powyższe pytanie prawidłowe jest pierwsze przypuszczenie, to chyba mam rozwiązanie:
16_03_02_13
05_10_12_06
07_04_08_11
09_15_14_01
dla którego występują wszystkie sumy od 30 do 39, każda dokładnie raz.
Gratulacje! Programem czy na piechotę? Podejrzewam, że na piechotę, bo gdyby było programem, to rozwiązań pojawiłoby się więcej.
mp
Dzięki dwóm postawionym przez Durera warunkom zadanie wydaje się nie być takie straszne…
12 8 3 13
6 10 11 2
9 5 7 16
4 15 14 1
sumy w rzędach: 36, 29, 37, 34,
sumy w kolumnach: 31, 38, 35, 32
przekątne: 30, 33
ciąg kolejnych sum: od 29 do 38
każda liczba w kwadracie (od 1 do 16) użyta raz
Czy to jest dobre rozwiązanie?
Bo wygląda na to, że jest ich sporo – imię jego czterdzieści i cztery!
Jest OK! Naprawdę są 44 rozwiązania?
mp
Rozwiązania z komputera (półtorej sekundy na leciwym laptopie).
Liczba porządkowa i kolejne wiersze oddzielone tabulatorami, na końcu w nawiasach kwadratowych najmniejsza suma (początek ciągu arytmetycznego) .
W trzech pierwszych rozwiązaniach zachowano nietknięty cały pierwszy wiersz!
1: 16 3 2 13 5 10 12 6 7 4 8 11 9 15 14 1 [30]
2: 16 3 2 13 12 4 6 8 9 11 7 10 1 15 14 5 [29]
3: 16 3 2 13 11 9 8 5 1 10 7 12 4 15 14 6 [30]
4: 16 3 2 9 10 8 11 6 1 13 7 12 4 15 14 5 [30]
5: 16 3 2 8 6 9 13 10 11 5 7 12 4 15 14 1 [29]
6: 16 3 1 13 5 10 8 9 4 11 7 12 6 15 14 2 [30]
7: 16 3 1 13 5 10 8 7 6 11 9 12 4 15 14 2 [30]
8: 16 3 1 13 4 10 11 5 9 8 6 12 2 15 14 7 [30]
9: 16 3 6 13 4 10 9 8 12 2 7 11 5 15 14 1 [29]
10: 16 3 6 13 8 10 9 4 11 5 7 12 2 15 14 1 [29]
11: 16 3 1 13 9 8 11 7 2 6 10 12 4 15 14 5 [30]
12: 16 3 6 13 4 9 10 8 11 2 7 12 5 15 14 1 [29]
13: 16 3 4 9 5 10 12 8 11 2 7 13 6 15 14 1 [29]
14: 16 3 7 12 4 10 11 8 9 2 5 13 6 15 14 1 [29]
15: 16 7 2 13 5 6 11 8 10 9 4 12 1 15 14 3 [29]
16: 16 4 2 13 5 12 11 8 6 7 10 9 3 15 14 1 [30]
17: 16 4 2 13 5 8 6 11 10 9 7 12 3 15 14 1 [29]
18: 16 7 2 13 6 5 11 8 9 4 10 12 1 15 14 3 [29]
19: 16 7 2 13 9 3 11 8 6 4 10 12 5 15 14 1 [29]
20: 16 6 2 13 10 4 11 5 9 7 8 12 3 15 14 1 [29]
21: 16 1 2 13 9 8 11 3 7 6 10 12 4 15 14 5 [30]
22: 16 5 2 13 4 11 7 8 3 6 10 12 9 15 14 1 [30]
23: 16 7 2 13 3 8 10 11 9 6 4 12 5 15 14 1 [29]
24: 16 7 2 13 8 11 10 6 9 3 5 12 4 15 14 1 [29]
25: 16 4 2 11 5 13 10 8 3 6 9 12 7 15 14 1 [30]
26: 16 1 2 11 7 10 13 3 9 6 8 12 4 15 14 5 [30]
27: 16 8 2 11 6 10 13 7 9 5 3 12 4 15 14 1 [29]
28: 16 6 2 11 8 10 13 7 9 5 3 12 4 15 14 1 [29]
29: 16 2 7 13 6 10 11 8 9 4 5 12 1 15 14 3 [29]
30: 16 5 4 13 6 10 11 8 12 2 7 9 3 15 14 1 [29]
31: 16 1 3 13 2 10 11 12 9 6 8 7 4 15 14 5 [30]
32: 16 5 4 13 8 10 11 6 9 7 2 12 3 15 14 1 [29]
33: 16 2 6 13 7 10 5 8 9 11 4 12 3 15 14 1 [29]
34: 16 2 5 13 4 10 9 8 3 6 11 12 7 15 14 1 [30]
35: 16 5 3 13 10 9 11 6 8 2 7 12 4 15 14 1 [29]
36: 16 2 6 9 3 10 11 8 13 4 7 12 5 15 14 1 [29]
37: 16 4 3 10 2 13 11 8 5 6 7 12 9 15 14 1 [30]
38: 16 5 7 10 3 11 13 8 9 6 2 12 4 15 14 1 [29]
39: 12 3 2 13 5 10 4 16 11 6 9 7 8 15 14 1 [29]
40: 11 3 2 13 5 10 7 16 12 9 8 6 4 15 14 1 [29]
41: 12 3 2 16 7 10 6 8 9 11 13 5 4 15 14 1 [30]
42: 13 7 2 16 6 10 11 8 9 4 5 12 3 15 14 1 [29]
43: 12 4 5 13 2 10 11 8 9 3 7 16 6 15 14 1 [29]
44: 12 8 3 13 6 10 11 2 9 5 7 16 4 15 14 1 [29]
Niespodzianka!
Magiczne 7 rozwiązań przy warunku, że można ruszyć tylko 6 liczb:
1: 16 3 2 13 1 10 12 8 9 7 5 11 4 15 14 6 [30]
2: 16 3 1 13 5 10 11 4 9 8 6 12 7 15 14 2 [30]
3: 16 3 1 13 5 11 10 4 9 6 7 12 8 15 14 2 [30]
4: 16 4 2 10 3 13 11 8 5 6 7 12 9 15 14 1 [30]
5: 16 1 3 13 2 10 11 7 9 6 8 12 4 15 14 5 [30]
6: 16 4 5 13 8 10 11 6 9 2 7 12 3 15 14 1 [29]
7: 11 3 2 13 6 12 10 8 9 5 7 16 4 15 14 1 [29]
Na przykład pierwsze rozwiązanie:
16 3 2 13
1 10 12 8
9 7 5 11
4 15 14 6
sumy: 34 31 32 39 (wiersze)
30 35 33 38 (kolumny)
37 36 (przekątne)
Liczby przesunięte (miejsca):
0000
1010
0111
0001
Istotnie, tylko 6 liczb ruszonych to dla mnie spore zaskoczenie. Musiałem się pomylić przy określaniu tego minimum.
mp
Dla potomności liczby rozwiązań w zależności od ilości liczb, które należy przesunąć:
1,2,3,4,5: 0
6: 7
7: 44
8: 149
9: 394
10: 1199
(dalej moje rozwiązanie robi się zbyt czasochłonne)
monitoryt 🙂 – fajne słówko
do zadanka siadam dopiero jutro w pracy 😉
Pierwsze rozwiązanie było znalezione komputerem. We wpisie umieściłem tylko jedno rozwiązanie, bo nie byłem pewny, że poprawnie zrozumiałem treść zadania.
Chwilowo brakuje mi nawet pomysłu, jak do tego usiąść na piechotę… może w wolnej chwili pomyślę.
Tymczasem komputer znalazł 44 rozwiązania:
1:
16_03_02_13
05_10_12_06
07_04_08_11
09_15_14_01
2:
16_03_02_13
11_09_08_05
01_10_07_12
04_15_14_06
3:
16_03_02_13
12_04_06_08
09_11_07_10
01_15_14_05
4:
16_03_02_08
06_09_13_10
11_05_07_12
04_15_14_01
5:
16_03_02_09
10_08_11_06
01_13_07_12
04_15_14_05
6:
16_03_06_13
08_10_09_04
11_05_07_12
02_15_14_01
7:
16_03_06_13
04_10_09_08
12_02_07_11
05_15_14_01
8:
16_03_06_13
04_09_10_08
11_02_07_12
05_15_14_01
9:
16_03_07_12
04_10_11_08
09_02_05_13
06_15_14_01
10:
16_03_04_09
05_10_12_08
11_02_07_13
06_15_14_01
11:
16_03_01_13
05_10_08_09
04_11_07_12
06_15_14_02
12:
16_03_01_13
05_10_08_07
06_11_09_12
04_15_14_02
13:
16_03_01_13
09_08_11_07
02_06_10_12
04_15_14_05
14:
16_03_01_13
04_10_11_05
09_08_06_12
02_15_14_07
15:
16_02_05_13
04_10_09_08
03_06_11_12
07_15_14_01
16:
16_02_06_13
07_10_05_08
09_11_04_12
03_15_14_01
17:
16_02_06_09
03_10_11_08
13_04_07_12
05_15_14_01
18:
16_02_07_13
06_10_11_08
09_04_05_12
01_15_14_03
19:
16_05_03_13
10_09_11_06
08_02_07_12
04_15_14_01
20:
16_05_02_13
04_11_07_08
03_06_10_12
09_15_14_01
21:
16_05_07_10
03_11_13_08
09_06_02_12
04_15_14_01
22:
16_05_04_13
08_10_11_06
09_07_02_12
03_15_14_01
23:
16_05_04_13
06_10_11_08
12_02_07_09
03_15_14_01
24:
16_08_02_11
06_10_13_07
09_05_03_12
04_15_14_01
25:
16_06_02_13
10_04_11_05
09_07_08_12
03_15_14_01
26:
16_06_02_11
08_10_13_07
09_05_03_12
04_15_14_01
27:
16_07_02_13
03_08_10_11
09_06_04_12
05_15_14_01
28:
16_07_02_13
05_06_11_08
10_09_04_12
01_15_14_03
29:
16_07_02_13
08_11_10_06
09_03_05_12
04_15_14_01
30:
16_07_02_13
09_03_11_08
06_04_10_12
05_15_14_01
31:
16_07_02_13
06_05_11_08
09_04_10_12
01_15_14_03
32:
16_04_03_10
02_13_11_08
05_06_07_12
09_15_14_01
33:
16_04_02_13
05_08_06_11
10_09_07_12
03_15_14_01
34:
16_04_02_13
05_12_11_08
06_07_10_09
03_15_14_01
35:
16_04_02_11
05_13_10_08
03_06_09_12
07_15_14_01
36:
16_01_03_13
02_10_11_12
09_06_08_07
04_15_14_05
37:
16_01_02_13
09_08_11_03
07_06_10_12
04_15_14_05
38:
16_01_02_11
07_10_13_03
09_06_08_12
04_15_14_05
39:
13_07_02_16
06_10_11_08
09_04_05_12
03_15_14_01
40:
11_03_02_13
05_10_07_16
12_09_08_06
04_15_14_01
41:
12_03_02_16
07_10_06_08
09_11_13_05
04_15_14_01
42:
12_03_02_13
05_10_04_16
11_06_09_07
08_15_14_01
43:
12_08_03_13
06_10_11_02
09_05_07_16
04_15_14_01
44:
12_04_05_13
02_10_11_08
09_03_07_16
06_15_14_01
Czy we fragmencie „…należy przestawić jak najmniej cyfr…” jest nieścisłość czy podpowiedź? Tzn. czy nie powinno być „…należy przestawić jak najmniej liczb…”?
🙂 nieścisłość (łagodnie mówiąc). Ciekawe jednak, jak wyglądałoby rozwiązanie, gdyby istotnie chodziło o cyfry.
m
16 4 3 10
2 13 11 8
5 6 7 12
9 15 14 1
Trochę szczęścia nie zaszkodziło: brute force znalazł po przeszukaniu niewiele ponad 3% permutacji (dzięki czemu młócił godzinę, a nie 30).
16__2__3_13
_9__5__7__8
_4_10_11_12
_1_15_14__6
Kwadrat ten jest antymagiczny. Liczby 15 i 14 pozostały na swoich miejscach. Ale niestety sumy nie są kolejnymi liczbami naturalnymi, chociaż niewielu brakuje (zamiast 33 jest 39).
Ten kwadrat spełnia już prawie wszystkie warunki, prócz ilości przestawień liczb
_10__4__3_13
_16__6__7__8
__1__9_11_12
__2_15_14__5
„należy przestawić jak najmniej liczb, czyli siedem” – a dlaczego siedem? 😉
Poniżej siedem rozwiązań z przestawionymi sześcioma liczbami. Mniej niż sześć już się nie da.
1:
16_03_02_13
01_10_12_08
09_07_05_11
04_15_14_06
2:
16_03_01_13
05_10_11_04
09_08_06_12
07_15_14_02
3:
16_03_01_13
05_11_10_04
09_06_07_12
08_15_14_02
4:
16_04_02_10
03_13_11_08
05_06_07_12
09_15_14_01
5:
16_04_05_13
08_10_11_06
09_02_07_12
03_15_14_01
6:
16_01_03_13
02_10_11_07
09_06_08_12
04_15_14_05
7:
11_03_02_13
06_12_10_08
09_05_07_16
04_15_14_01
16,3,1,13
5,11,10,4
9,6,7,12
8,15,14,2
16 4 2 11
5 13 10 8
3 6 9 12
7 15 14 1
wydaje się być rozwiązaniem zarówno w przypadku, gdy przestawiamy liczny, jak i cyfry (po prostu liczby dwucyfrowe zamieniamy między sobą a jednocyfrowe między sobą)
Zadanie ma 11 rozwiązań. W tym 7 gdzie suma sum liczb z wierszy, kolumn i przekątnych jest równa 335 i 4, gdzie ta suma wynosi 345.
Rozwiązania:
1)
12 3 2 13
5 10 4 16
11 6 9 7
8 15 14 1
2)
16 1 2 13
9 8 11 3
7 6 10 12
4 15 14 5
3)
16 2 5 13
4 10 9 8
3 6 11 12
7 15 14 1
4)
16 2 6 13
7 10 5 8
9 11 4 12
3 15 14 1
5)
16 2 7 13
6 10 11 8
9 4 5 12
1 15 14 3
6)
16 3 1 13
4 10 11 5
9 8 6 12
2 15 14 7
7)
16 3 2 9
10 8 11 6
1 13 7 12
4 15 14 5
8)
16 5 3 13
10 9 11 6
8 2 7 12
4 15 14 1
9)
16 5 4 13
8 10 11 6
9 7 2 12
3 15 14 1
10)
16 6 2 13
10 4 11 5
9 7 8 12
3 15 14 1
11)
16 7 2 13
6 5 11 8
9 4 10 12
1 15 14 3
A jednak te dwa warunki, a właściwie jeden, ponieważ drugi wydaje się być koniecznością, sprawiają, że zadanie jest straszne…
Po dwóch godzinach komputer wypluł 17468 kwadratów antymagicznych, w których 1514 znajduje się w odpowiednich miejscach.
Spośród nich można wybrać siedem, które różnią się od Durerowego na tylko 6 pozycjach.
Na przykład:
11 3 2 13
6 12 10 8
9 5 7 16
4 15 14 1
16 1 3 13
2 10 11 7
9 6 8 12
4 15 14 5
Takich, które różnią się na siedmiu pozycjach (jak prosił autor) jest czterdzieści i cztery 🙂
Pozdrawiam
Piotr
Koniecznie trzeba zlecić rozwiązanie tego zadania politykom i niech żaden się nie odezwie, dokąd tego nie rozsupła. I wreszcie zapanuje pokój, ład i porządek.
Czyli – czytelnicy „Polityki” górą!
Zajrzałem wczoraj – widzę ciekawe zadanie. No to zabrałem się za pisanie programu. 🙂
Zaglądam dzisiaj – niestety spóźniłem się. 🙁
Pozostaje mi potwierdzić wyniki uzyskane przez moich szanownych poprzedników.
Dopowiem tylko, że mój program nie sprawdzał wszystkich 14! permutacji, a jedynie te, zgodne z warunkami. Najpierw tworzył kombinację 14 po 7, a następnie z tych siedmiu liczb tworzył permutacje i wybierał te będące nieporządkiem (czyli takie, w której żaden element nie znajduje się na swoim miejscu). Razem daje to (14 po 7)* !7 = 6 362 928 układów do sprawdzenia (zamiast 14!=87 178 291 200).
A ja napisałem program generujący wyniki przy dodatkowym i nieuprawnionym założeniu o tym, że pierwsza podmieniana liczba wstawiana jest na miejsce drugiej, druga na miejsce trzeciej, itd. aż siódma na miejsce pierwszej. Dlatego wyszło mi 11 rozwiązań. Pełna liczba rozwiązań to rzeczywiście 44 + 7.
Ja zrobiłem mniej więcej tak, jak to opisał Witman, tyle że najpierw wygenerowałem wszystkie permutacje zbioru 7-elementowego, które nie pozostawiają żadnego elementu na swoim miejscu i gdzieś je sobie zapisałem – ich jest znacznie mniej niż 7!. Potem wygenerowałem wszystkie kombinacje pozostałych 7 elementów z 14 i dla każdej sprawdziłem każdą z permutacji wygenerowanych w poprzednim punkcie. Sprawdzenie warunku o ciągu arytmetycznym tworzonym przez sumy najłatwiej sprawdzić po ich uporządkowaniu. W ten sposób można uzyskać program działający w czasie poniżej 2 sekund.