Kwadratowo
Przeglądam stare numery – sprzed ponad półwiecza – angielskich pisemek z krzyżówkami i łamigłówkami. Forma jest mocno retro, ale treść prawie wcale się nie zestarzała. Sporo w nich zagadek typu mensowego, czyli polegających na uzupełnianiu braków. Kłopot z tym, że rozwiązania są w następnych numerach, a ja mam tylko kilkanaście niekolejnych.
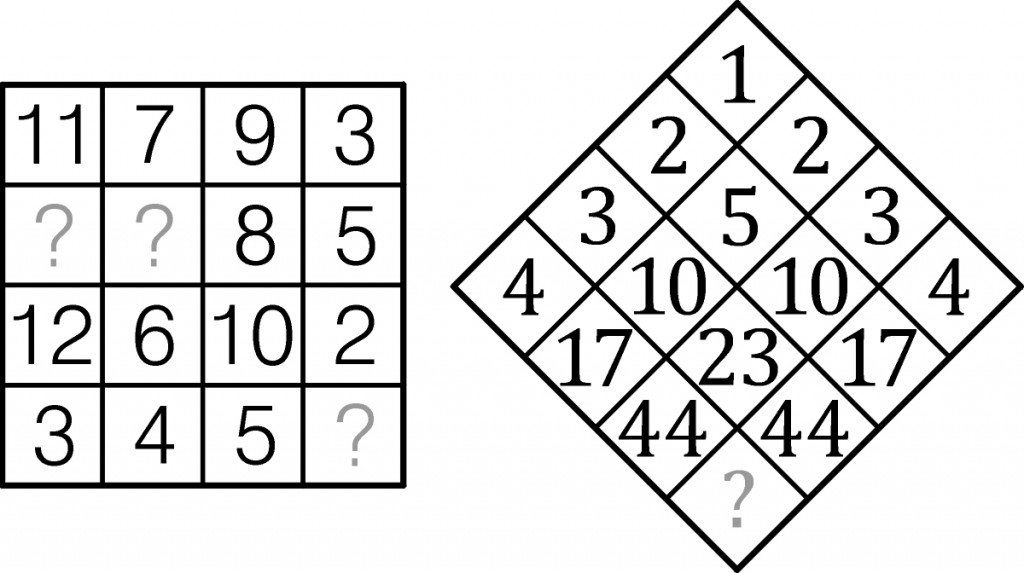
Oto dwa „kwadratowe” zadania, których rozgryzanie zajęło mi sporo czasu (no i nie mam pewności, czy jest takie, jak należy). Nie wątpię, że Państwu pójdzie szybciej. W obu chodzi o wpisanie w pola ze znakiem zapytania właściwych liczb, czyli takich, aby zasada rządząca całym układem była zachowana.
Za rozwiązanie obróconego kwadratu można było wygrać 10 funtów. Na przełomie lat 50. i 60. była to całkiem przyzwoita sumka (średnia miesięczna pensja wynosiła wówczas 65 funtów).
Na marginesie: gdybym zapytał, który kwadrat jest większy, to pewnie każdy odpowiedziałby, że obrócony; tymczasem oba są równe (złudzenie apteczne? 🙂 )

Komentarze
…już witałem się z gąską… a tu te ’44’! 🙂
Czyżby 105 w obróconym kwadracie…? Muszę to jeszcze przemyśleć…
W pierwszym kwadracie od góry do dołu, od lewej do prawej:
2; 15; 18.
W tego typu zadaniach chyba przy odrobinie wysiłku można znaleźć więcej pomysłów na rozwiązanie. Ten jest chyba najprostszy.
Czyżby w drugim zadaniu reguła była taka jak poniżej?
Liczba w polu jest sumą liczb z trzech pól położonych powyżej, najbliżej danego pola jak to możliwe, przy czym jedno z pól musi leżeć przy którejś z górnych krawędzi kwadratu?
Jeżeli nie istnieją pola spełniające powyższe warunki, do danego pola wpisuje się kolejną liczbę naturalną.
Nie wiem czy to nie za bardzo naciągane, ale daje niezłe rezultaty 😉
10 funtów nawet dzisiaj nie jest złe 😉 numer konta przesłać na priv?
Kwadrat 1 od góry od lewej: 6, 13, 20
Kwadrat 2: 97
Prawy kwadrat od razu widać: 93. Każda liczba jest równa sumie dwóch bezpośrednio powyżej plus numer wiersza. Wiersze są tak numerowane by dwójki były w wierszu zerowym.
Lewy kwadrat zajął mi trochę czasu: 6, 1, 8. Każdy podkwadrat 2×2 ma sumować się do 25.
Brawo! Pierwsza poprawna para odpowiedzi.
mp
93?
W pierwszym będzie 7, -11 i -10?
6, 1, 8. 105?
Dlaczego 105?
mp
My tu szukamy jakichś ciągów i sum a to jest zaszyfrowany klucz do odkodowania instrukcji przez agentów MI5 w jakimś afrykańskim kraju, którzy właśnie sposobią się do dokonania tam przewrotu…:)
Z którego roku jest ta gazeta ? 😉
1961
mp
To może chociaż 91 w drugim kwadracie? 😛
Liczba w kratce jest sumą dwóch liczb powyżej niej i najbardziej skrajnie położonej z co najwyżej trzech sąsiadujących z tymi dwiema z rzędu o jeden wyżej. Zasada pasuje do wszystkich poza skrajnymi. Ale chyba trochę naciągana 😉
Raczej tak, bo można prościej.
mp
a) 6, 1, 8
b) 99
Dlaczego 99?
mp
Proszę o moderację komentarzy, bo koledzy mi wprowadzają zamęt 🙂
Moderuję, tzn. uwalniam niepoprawne.
mp
93.
Lewy diagram: na zmianę liczby w trzecim rzędzie są większe bądź mniejsze od tych z rzędu pierwszego o 1. Z trzeciej kolumny wynika, że analogiczna różnica dla rzędów drugiego i czwartego wynosi 3. Będzie więc od lewej: 6, 1 i 8. Co ciekawe: suma liczb w każdej ćwiartce kwadratu wyniesie wtedy 25.
Żartuję… z drugiej strony, w tym przypadku „niepoprawne” znaczy niezgodne z Pana rozwiązaniem. Musi więc Pan mieć mocne argumenty, że dopasowanie zgadującego jest gorsze.
Mam mocne (chyba 🙂 )
mp
1961 i wszystko jasne, atak w Zatoce Świń na Kubie 🙂
W pierwszym 6,1,8
W drugim kwadracie obstawię 85 😉
Pierwszy kwadrat:
Sumy w wierszach i kolumnach są równe 30 lub 32.
(32 – w pierwszej i trzeciej kolumnie, 30 w drugiej i czwartej;
(30 – w I i III wierszu a 32 w II i IV)
Dlatego w drugim wierszu należy dopisać liczby 6 i 13, a w czwartym 20.
No tak… Po treści wpisu można było się domyślić, że reguła powinna być niebanalna i znacznie bardziej elegancka…
Cóż… Pomyślę to może wymyślę 😉
Dlaczego 99? Nie wiem dlaczego.
Chciałem znaleźć rozwiązanie korzystając z relacji pomiędzy pewnymi ciągami, ale nie potrafię teraz przypomnieć sobie mojego rozumowania dla którego otrzymałem ?=99, więc pewnie było ono błędne.
Przypuszczam, że oczekiwanym wynikiem jest ?=93.
Sposób rozwiązania jest podobny do tego z zadania pierwszego i oparty jest on na punktach węzłowych (miejsca styku czterech liczb). Punktom węzłowym można przypisać, po ustaleniu pewnej reguły, liczby. Mając już znalezione liczby węzłowe, możemy, po uwzględnieniu dodatkowego warunku, ustalić, że
(?+23)-(44+44)=28(punkt węzłowy)
?=93
antyp dokładnie tak!
w drugim kwadracie reguła jest nieco bardziej skomplikowana, mianowicie:
1 warstwa, to kolejne cyfry od 1 do 4;
2 warstwa, to suma liczb, będących bezpośrednio nad nią, uwzględniając też tą stykającą się samym rogiem;
3 i 4 warstwa, to suma liczb: będącej bezpośrednio nad nią, stykającą się samym rogiem, oraz liczb, które z tą drugą stykają się ścianką pomniejszona o sumę liczb położonych po lewej i prawej stronie liczby, która styka się samym rogiem z tą będącą nad naszą liczbą (dla 23 będzie to: 10+10+5+2+2-3-3)
A pan Marek mój pierwszy komentarz zapewne uwolnił omyłkowo 😉
Drugi kwadrat trzeba oprotestować, bo logika mówi, że powinno być 25 zamiast 23 i 52 zamiast 44. Owa rozbieżność natrętnie wbija się w mózg i prowadzi jedynie do frustracji, że z tymi 23 i 44 nic nie pasuje. Z liczbami pierwszymi np. też nic… Wczoraj wymyśliłem, że może być 91, więc napiszę, żeby nie oddawać całkiem walkowera, ale tak naprawdę to tam nic nie pasuje…
W drugim kwadracie obstawiam 93
Reguła: liczby na górnych bokach kwadratu to kolejne liczby naturalne. Pozostałe powstają jako suma wartości z obu górnych sąsiadów (sąsiadujących całym bokiem) oraz numeru kolejnego wiersza.
Mamy;
Pierwszy wiersz: 5 = 2 + 2 + 1
Drugi wiersz: 10 = 3 + 5 + 2
Trzeci wiersz: 17 = 4 + 10 + 3 oraz 23 = 10 + 10 + 3
Czwarty wiersz: 44 = 17 + 23 + 4
Piąty wiersz: ? = 44 + 44 + 5 = 93
Otóż to.
mp
Anglicy mają zwoje mózgowe zakręcone z lewej na prawo i dla tego nam z kontynentu tak trudno się wczuć w ich poczucie humoru i logikę 😉
Moim zdaniem w 2 kwadracie będzie 93.
Nad pierwszym czas pomyśleć…
p.s. liczba równa jest sumie dwóch liczb powyżej i numeru ‚rzędu’ licząc od góry i od zera.