Pento-szyfr

26 września 2012
Marek Penszko

W komentarzach do poprzedniego wpisu kilkakrotnie padło pytanie o to, w jaki sposób układa się takie zadania – chodziło oczywiście o zamieszczoną w tym wpisie odmianę sudoku. Autor, którego poprosiłem o odpowiedź, odpisał, że… nie wie, natomiast może wyjaśnić, jak jemu udało się tego dokonać. Otóż z grubsza robimy tak:

Bierzemy rozwiązanie zwykłego „antykońskiego” sudoku, dzielimy diagram na nieregularne 9-polowe obszary tak, aby w każdym znalazło się 9 różnych cyfr, usuwamy prawie całe rozwiązanie, tzn. pozostawiamy z niego „na czuja” 8 różnych cyfr i w ten sposób mamy gotowy „szkic do portretu”. Teraz trzeba sprawdzić, ile rozwiązań ma taki szkic, a następnie wybrać jedno z nich i spróbować dopisać jak najmniej cyfr tak, aby było jedno rozwiązanie osiągalne na logikę. Tutaj przydaje się – i to bardzo – rozwiązujący takie zadania program komputerowy, który autor napisał. Program sprawdza, czy po dopisaniu jakiejś cyfry rozwiązanie będzie jedno, czy więcej. Nie sprawdzi jednak, czy do rozwiązania wystarcza logika – tu potrzeba dużo cierpliwości w rozwiązywaniu na piechotę i nie mniej szczęścia. W sumie to niezły kawałek nielekkiej, ale dającej dużo satysfakcji harówki (jeśli efekt jest zadowalający).

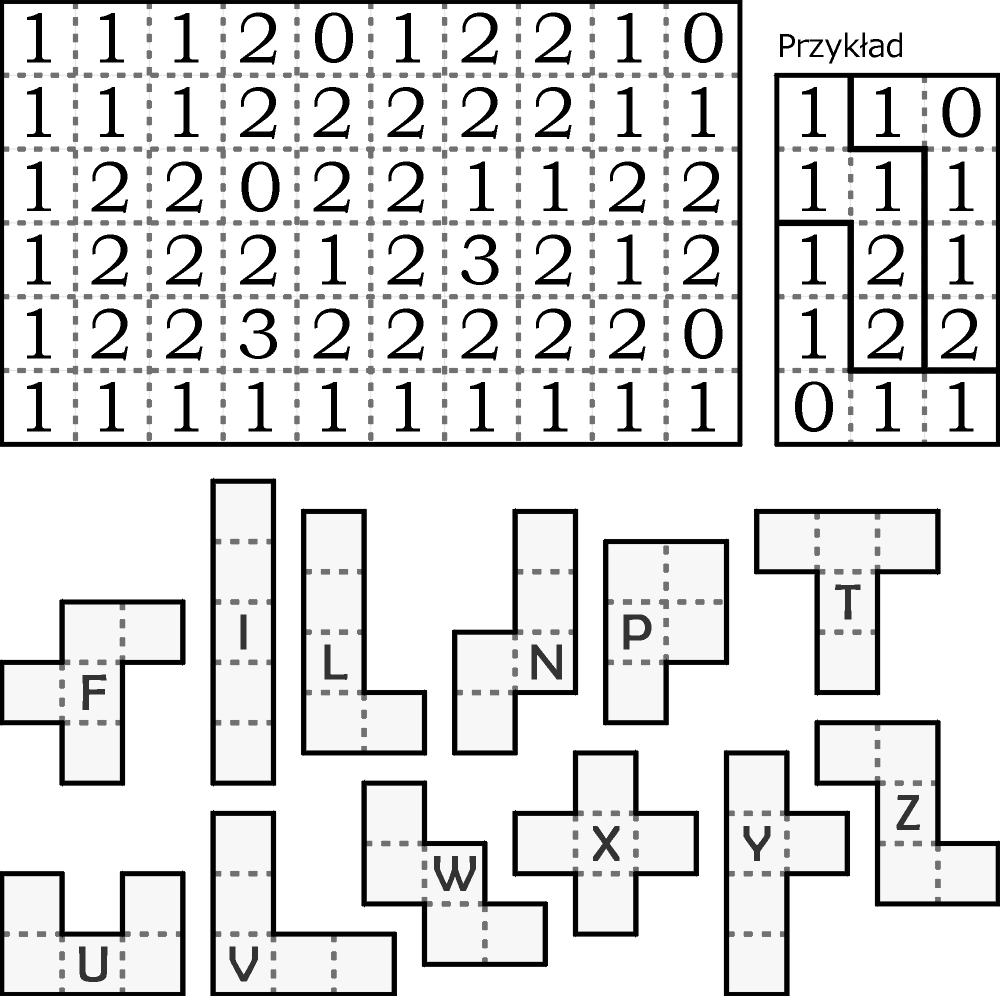
Dla odmiany proponuję jeszcze jedno zadanie Michała Stajszczaka, które otrzymałem od niego dawno temu. Napisałem „dla odmiany”, ponieważ wygląda na to, że takie zadanie powstaje niemal samo – wystarczy wybrać jeden z 2339 prostokątów 6×10 ułożonych z kamieni pentomina, „zaszyfrować” go, wpisując odpowiednie liczby (0, 1, 2, 3) w kwadraciki i – gotowe. Mogę się jednak mylić w kwestii samopowstawania, jeżeli są różne układy kamieni, którym odpowiada jednakowy układ cyfr (nie wgłębiałem się w temat, a warto, bo wiążą się z nim ciekawe problemy, np. dlaczego suma liczb dla prostokąta 6×10 jest zawsze taka sama = 87). Z drugiej strony zapewne nie zawsze jest konieczne wpisywanie cyfr we wszystkie kwadraciki, aby rozwiązanie było jednoznaczne. Jak by nie było, pomysł zadania, choć prosty, jest przedni.

Prostokąt należy podzielić na 12 znajdujących się pod nim figur (kamieni) pentomina (dozwolone są ich lustrzane odbicia). Cyfra w kwadraciku oznacza, z iloma innymi figurami sąsiaduje bokami ten kwadracik.

W rozwiązaniu – gdyby ktoś chciał się takowym pochwalić – wystarczy podać literowe nazwy kamieni, sąsiadujących z dokładnie trzema kamieniami.

Komu przypadła gra „Rancho” za rozwiązanie zakręconego sudoku, podam w następnym wpisie.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.