Numeracja oczko
Jednego z zadań konkursowych zamieszczonych w majowym „Świecie Nauki” poprawnie nie rozwiązał nikt. W ogóle spośród 117 osób uczestniczących w konkursie tylko 14 podjęło wyzwanie, ale poległo, pomijając jeden z warunków. Szczerze mówiąc, nie dziwi mnie to, bo rzecz jest karkołomna, a w dodatku ubrana była w fabułkę nieco utrudniającą dotarcie do meritum (no a poza tym nagrodami w konkursach są umiarkowanie kuszące skarby z wyższej półki – książki).
Pominę „mięsko”, czyli wspomnianą fabułkę i bardzo krótko przedstawię „szkielet” zadania w nadziei, że ktoś z Państwa spróbuje twardy orzech rozgryźć.
Mamy prostokąt 5×4:
Jak ponumerować pola liczbami od 1 do 20 w taki sposób, aby różnica między liczbami w sąsiednich polach (także stykających się tylko rogami) nigdzie nie była mniejsza niż 4?
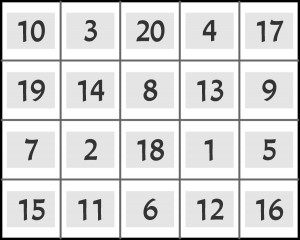
Można to zrobić na wiele sposobów, np. tak:
A teraz majowy orzech, który różni się od powyższej pestki tym, że różnica między sąsiednimi liczbami (przypominam: także sąsiadującymi przez róg) powinna być nie mniejsza niż 5. Ale nie tylko tym, bo wówczas rozwiązania by nie było. Zakres numerów jest tym razem większy – od 1 do 21. Oczywiście jedna z liczb zostanie przy numeracji pominięta.
Formalnie sprawa jest prosta, a i merytorycznie nie wydaje się, aby stawiła duży opór. Pozory mylą. Będę bardzo mocno i bardzo mile zaskoczony, jeśli ktoś znajdzie rozwiązanie.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.

Komentarze
Ostatnie zdanie zmobilizowało mnie, chyba ze dwie godziny już zajęło mi to zadanie. W najlepszym razie zostawały mi dwa wolne pola. Myślę, że bez komputera lub łutu szczęścia, zadanie jest nie do rozwiązania… ja mam dosyć, ale coś nadal każe mi wpisywać liczby w kratki…
Wydaje mi się, że komputer niewiele może tu pomóc. W każdym razie nie mam dobrego pomysłu, jak go zaprząc do roboty.
mp
Łamigłówka zabójcza. Idzie się w kółko i wszystko wydaje się na dobrej drodze aż tu pod koniec … klops.
Od strony informatycznej problem jest dośc dobrze zdefiniowany. Jest to tak zwany izomorfizm podgrafu.
Mamy dany graf G, którego wierzchołkami są liczby od 1 do 21 a krawędź istnieje pod warunkiem, że różnica jest niemniejsza od 5.
I drugi graf F, który odpowiada kratkom diagramu z krawędziami pomiędzy sąsiadującymi kratkami.
I pytanie czy istnieje podgraf G izomorficzny z F.
Problem jest oczywiście NP zupełny.
Ale na razie spróbuję rozwiązać na piechotę.
Pozdrawiam
Piotr
W pierwszej chwili myslałem, że trzeba zaprząc do tego komputer, ale po chwili zastanowienia okazało się, że zadanie jest śmiesznie łatwe:
17_12_18_13_19
_6__1__7__2__8
14_20_15_21_16
_3__9__4_10__5
Michale, gratuluję. Nikt dotąd nie nazwał tego zadania śmiesznie łatwym, ani nawet łatwym, a tym bardziej nie stwierdził, że chwila zastanowienia wystarczy, aby je rozwiązać. Po raz pierwszy ukazało się ono przed kilkunastu laty na łamach magazynu Discover jako supertrudne, a jego autor podtrzymuje tę opinię. Sądzę, że nie tylko on byłby zainteresowany wyjaśnieniem, dlaczego Twoim zdaniem to jest śmiesznie łatwe, tzn. jaki sposób rozwiązywania wynika z chwili zastanowienia.
mp
Wpisanie w prostokąt liczb nie wydaje się zadaniem bardzo trudnym. Można to zrobić na przykład tak:
11, 17, 12, 18, 13
6, 1, 7, 2, 8
19, 14, 20, 15, 21
3, 9, 4, 10, 5.
Podejrzewam, że istotnym elementem, który przyczynił się do braku rozwiązania zadania z majowego Ś.N. mogła być niełatwa do zrozumienia fabułka zadania.
PS Jestem zaskoczony ilością osób uczestniczących w konkursie. Widać, że łamigłówkologia trzyma się mocno.
Andrzeju, gratuluję i mam prośbę o kilka słów na temat sposobu rozwiązywania – jeśli oparty był na logice, a nie na próbowaniu, intuicji lub natchnieniu ;).
mp
17,12,18,13,19
_6,_1,_7,_2,_8
14,20,15,21,16
_3,_9,_4,10,_5
Przy okazji tego zadania rodziło się mnóstwo teorii, które szybko legły w gruzach. Jedną z najbardziej obiecujących była teoria kamieni domina z polami o 5 większymi 1-6, 2-7… ale pozwalała na ułożenie planszy z 2 wolnymi polami, następnie były inne układy oczek, ale wygrała inna teoria 🙂 wszystkie za to miały część wspólną: brak 11.
No i teoria kości domina sprawdziła sie częściowo: kości miały pola o 5 większe na sąsiednich częściach kości, oprócz dwóch kości gdzie różnica wynosiła ową brakującą 11 🙂
Zadanie nazwałem „śmiesznie łatwym”, ponieważ wystraszony ostatnim zdaniem opisu (będę bardzo mocno zaskoczony, gdy ktoś znajdzie rozwiązanie) oraz komentarzami Wiąza i Piotra, spodziewałem się złożonego zagadnienia programistycznego.
Ale zawsze w takich sytuacjach sprawdzam z grubsza, ile wariantów komputer musiałby sprawdzić i jak zrobić, żeby było ich jak najmniej. Dlatego zacząłem się zastanawiać, co najpierw zrobić „ręcznie”. Przyjąłem założenie, żeby wywalić 11, a skrajne liczby (1, 2, 20 i 21) umieścić w drugim i trzecim wierszu w drugich kolumnach od lewej i od prawej. Dlaczego tak? Sześć środkowych kratek ma po ośmiu sąsiadów, więc najlepiej, żeby były tam liczby, które mają mało różniących się o mniej niż 5. Potem pomyślałem, że liczby bliskie środka (9, 10, 12 i 13) trzeba umieścić w dolnym i górnym wierszu. A skoro po umieszczeniu 1 i 2 w drugim wierszu, 3, 4 i 5 musiały trafić do dolnego, do którego wpisałem też 9 i 10, to nie zostało nic innego niż przyjąć, że układ liczb 12-21 może być symetryczny do 1-10 i zadanie samo się rozwiązało.
Nie wiem, ile czasu mi to zajęło – 5 może 10 minut. W Łamiblogu często były zadania znacznie bardziej czasochłonne i stąd to określenie „śmiesznie łatwe”. Nie wiem też, ile w opisanej metodzie było logiki, a ile intuicji czy szczęścia w podejmowaniu decyzji. Zresztą nawet jeżeli to była intuicja, to być może ta intuicja oparta była na doświadczeniu w rozwiązywaniu łamigłówek (kiedyś jeden z brydżystów napisał, że w grze brydża intuicja oparta jest na doświadczeniu).
Mój sposób rozwiązywania polegał na próbowaniu. Podczas prób, zauważyłem, że kolejne liczby należy umieszczać w takich miejscach diagramu, aby „przecinały” one „grube” obszary pustych pól.
Sytuacja na diagramie po wstawieniu pierwszych dziesięciu liczb będzie wyglądała następująco:
X, X, X, X, X
6, 1, 7, 2, 8
X, X, X, X, X
3, 9, 4, 10, 5
Teraz, patrząc na częściowo wypełniony diagram, widzimy, że puste obszary są „cienkie”, a nie „grube”, więc łatwiej wypełnić je pozostałymi liczbami.
Przypuszczam, że powyższe wyjaśnienie sposobu wpisywania liczb do diagramu jest niezrozumiałe, więc obok próbowania dołożyłbym jeszcze intuicję, coś jeszcze, oraz, wbrew pozorom, odrobinę logiki.
19 13 18 12 17
8 2 7 1 6
16 21 15 20 14
5 10 3 9 4
Pierwsze rozwiązanie znalezione w niecałe 7 minut, po napisaniu programu (około 2 godziny, w tym optymalizacja) w prologu, którego zacząłem się uczyć – polecam 🙂
3 9 4 10 5
14 20 15 21 16
6 1 7 2 8
11 17 12 18 13
Swoją drogą ładne, „symetryczne” rozwiązanie…
… i najelegantsze 🙂 , bo przerwa pojawia się najpóźniej (brak 19).
mp
Ja uważam, że najelegantsze jest moje rozwiązanie 🙂
Uzasadnienie: suma liczb w wierszach skrajnych i środkowych jest taka sama, sumy liczb w kolejnych kolumnach stanowią postęp arytmetyczny, a suma liczb w środkowej kolumnie to czterdzieści i cztery 🙂
Tak na szybko wydaje mi się, że może brakować dowolnej liczby od 3 do 19.
Próbowałem też policzyć ilość możliwych rozwiązań, ale zbyt długo to trwało i nie skończyłem…
Czekam na kolejne podobne 🙂
A może w tzw. międzyczasie ktoś zechce spróbować ?:
Jak ponumerować pola prostokąta o wymiarach 6×5 liczbami od 1 do 30 w taki sposób, aby różnica między liczbami w sąsiednich polach (także stykających się tylko rogami) nigdzie nie była mniejsza niż 7?