Drzeworzędy
Przywiązałem się do drzew, więc jeszcze przez chwilę na ten temat.
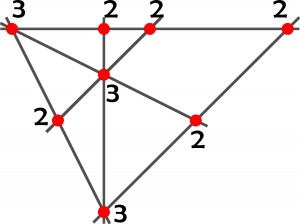
Drzewo jakie jest, każdy widzi. Przynajmniej trzy drzewa na jednej prostej to rząd. A drzeworząd? To dziwne określenie wiąże się z zadaniem, z którym nie mogę się rozstać od dwóch wpisów. Drzeworząd to drzewo-w-rzędzie, ale – drzewo na przecięciu dwóch rzędów, to dwa drzeworzędy, na przecięciu trzech – trzy itd. Jeśli więc posadzimy np. 8 drzew w 6 rzędach – tak, jak poniżej – i obok każdego wpiszemy liczbę równą liczbie rzędów, w których dane drzewo się znajduje,
to suma wszystkich liczb będzie równa liczbie drzeworzędów danego układu, czyli w tym przypadku 19.
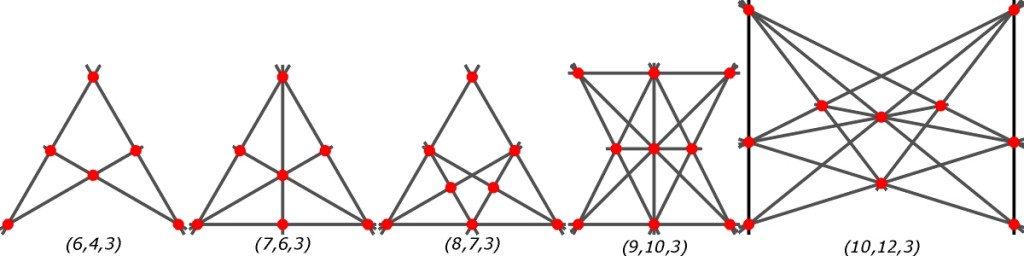
W tzw. problemie sadzenia drzew, „wyrosłym” na pograniczu geometrii dyskretnej i kombinatorycznej, chodzi o posadzenie n drzew w jak największej liczbie rzędów r po k drzewa w każdym rzędzie. Poniżej rozwiązania dla k = 3 i n = 6, 7, 8, 9 i 10.
Liczba drzeworzędów d w każdym z tych rozwiązań równa jest k*r.
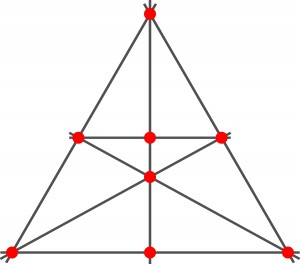
Czy jeśli pominiemy k i zapytamy o maksymalną wartość d dla danego n, to wynik będzie zawsze taki sam, jak w problemie sadzenia drzew? Z zadania goszczącego w dwóch poprzednich wpisach wynika, że nie, bowiem dla n = 8 wartość d może być o jeden większa, niż to wynika ze wzoru k*r, a więc równa 22 – w jednym rzędzie mogą znaleźć się 4 drzewa:
Jest to najmniejsza wartość d większa od tej, która wynika z problemu sadzenia drzew – czyli dla danego n, ale z pominięciem warunku, że liczba drzew k w każdym rzędzie powinna być jednakowa. Co ciekawe, jest to, jak dotąd, jedyny znany mi taki przypadek. Inaczej mówiąc, nie udało mi się zwiększyć liczby drzeworzędów w rozwiązaniu problemu sadzenia drzew dla żadnej innej wartości n i k. Gdyby ktoś z Państwa bliżej zainteresował się tym zagadnieniem i przeskoczył o jedno oczko jakieś inne d (dla danego n) wynikające ze wzoru k*r, to wdzięczny będę za informację.
A dla wszystkich znacznie prostsze zadanie, będące jakby odwrotnością problemu sadzenia drzew.
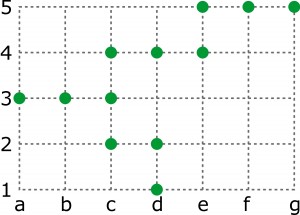
Na planie sadu drzewa znajdują się tylko w 12 węzłach siatki kwadratowej 5×7. Proszę oznaczyć trzy węzły, w których należy posadzić jeszcze 3 drzewa tak, aby po tej czynności żadne 4 z 15 drzew nie rosły w jednym rzędzie. Należy jednak zrobić to tak, aby zachowany był następujący warunek: od każdego drzewa do każdego innego powinno być możliwe dojście po liniach siatki bez konieczności przechodzenia przez „bezdrzewny” węzeł. Inaczej mówiąc, układ drzew powinien być spójny.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.

Komentarze
1) a2,e1,f1
2) e1,f1,f2
„Drzeworząd to drzewo-w-rzędzie, ale – drzewo na przecięciu dwóch rzędów, to dwa drzeworzędy”? Moim zdaniem „drzeworząd” to rząd drzew (rząd jest tu rdzeniem wyrazu), natomiast drzewo w rzędzie nazwałbym raczej: „rządodrzewem”.
W sumie określenie „drzeworząd” można by użyć, jeśli potraktować je jako wielkość, w jakiej jest liczona bytność drzewa w rzędach , bo trudno mi się zgodzić, że: „drzewo na przecięciu dwóch rzędów, to dwa drzeworzędy”, może tak: „drzewo na przecięciu dwóch rzędów ma wartość dwóch drzeworzędów (bo znajduje się w dwóch drzeworzędach)”.
Wiązie, jak zwał, tak zwał – istotne, że wiadomo, o co chodzi.
I „drzeworząd” i „rządodrzew” trochę mi zgrzytają, ale ten pierwszy mniej.
„Drzeworząd” to (potencjalne) sprzężenie drzewa z rzędem. Np. drzewo x w rzędzie a to drzeworząd xa; drzewo x na przecięciu rzędów a i b to dwa drzeworzędy – xa i xb. Tak to widzę.
mp
E1, F1, F2 (b. latwe)
a
To prostsze zadanie ma aż 4 rozwiązania?
Zapomniałem o rozwiązaniach:
1) a(1,2),e1
2) b(1,2),e1
3) a2, (e,f)1
4) b2, (e,f)1
Trochę przydużo. Na przekątnych też powstają rzędy.
mp
A ja znalazłem 😉 dla n=4 🙂 normalnie d=3, ale bez ograniczenia dla k=3, mamy d=4 przy umieszczenie tych 4 drzew w jednej linii.
Albo takie proste albo czegoś nie zrozumiałem:
a2
e1
f1
Ech te przekatne, w takim razie zostaje tylko jedno.
Oj, niestety, nie. Aż tak idealnie nie jest, tzn. jeszcze by się coś znalazło.
mp
No tak, jeszcze 1(e,f),2f.
Mam pytanie: dlaczego przekątne są uprzywilejowane? W treści nic nie było o przekątnych, poza tym siatka oraz warunek spójności drzew sugeruje rzędy pionowe i poziome. A więc dlaczego rząd: a2,c3,e4,g5 już nie jest rzędem???
Oczywiście, że jest! Czyli (mea culpa) rozwiązanie jest jednak jedno.
mp