Pentagram bez magii
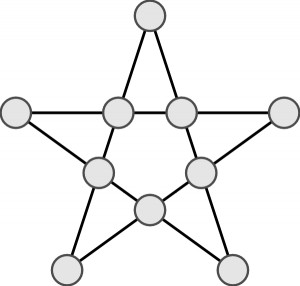
Pod koniec XIX wieku Dudeney jako pierwszy sięgnął gwiazd – magicznych i logicznych oczywiście. Zaczął od pięcioramiennej, czyli od pięciokąta gwiaździstego zwanego też pentagramem:
i wymyślił łamigłówkę, która po rzuceniu okiem na rysunek właściwie wymyśla się sama:
Liczby od 1 do 10 wpisz do kółek tak, aby suma czterech liczb na każdym boku pięciokąta była jednakowa.
Arytmetycznie niby wszystko gra. Suma liczb = 55, każda znajdzie się na dwóch bokach, czyli suma pięciu sum wyniesie 110, a zatem na każdą sumę czterech liczb przypadnie 22. Okazało się jednak, że zadanie byłoby dobre, ale na prima aprilis, bowiem z kombinatorycznego punktu widzenia sprawa się rypie. Krótko mówiąc, rozwiązania, czyli klasycznego pentagramu magicznego nie ma i nie tak łatwo to udowodnić, tzn. jest z tym trochę dłubaniny. Spróbujmy przeprowadzić taki dowód możliwie sprytnie i bezboleśnie.
Czwórkowych zestawów wybranych z kompletu 1-10, których suma równa jest 22, mamy 18:
(10,9,2,1) (10,8,3,1) (10,7,4,1) (10,7,3,2) (10,6,5,1) (10,6,4,2) (10,5,4,3) (9,8,4,1) (9,8,3,2) (9,7,5,1) (9,7,4,2) (9,6,5,2) (9,6,4,3) (8,7,6,1) (8,7,5,2) (8,7,4,3) (8,6,5,3) (7,6,5,4).
Załóżmy na wstępie, że na jakimś boku znajdzie się pierwsza czwórka – (10,9,2,1). Wtedy za pośrednictwem 10 musiałaby się z nią łączyć czwórka (10,5,4,3), bo inne czwórki zawierają wykorzystaną już liczbę 1 lub 2. Niestety, wówczas dziewiątki z pierwszej czwórki nie da się już z niczym skrzyżować, bo wszystkie pozostałe kwartety z dziewiątką zawierają albo jedną liczbę z pierwszej czwórki (1 lub 2) albo dwie z drugiej (3 i 4).
Czyżby koniec dowodu? Prawie, bo wypadałoby jeszcze dowieść, że założenie wstępne w istocie nie jest założeniem, tylko koniecznością, czyli czwórka (10,9,2,1) musi się znaleźć w gwieździe, jeśli miałoby istnieć rozwiązanie. Wbrew pozorom udowodnienie tego jest dość proste i krótkie, jeżeli wpaść na pomysł. Kto wpadnie?
A może ktoś zaproponuje jakiś inny w miarę prosty dowód, że magiczny pięciokąt gwiaździsty z liczbami od 1 do 10 nie istnieje.
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Obawiam się, ze mój dowód jest zbyt długi i niezbyt pomysłowy, ale:
jeżeli wybierzemy czwórkę z 10 bez 9 to możemy wybrać dwie czwórki na dwa sposoby: 10,8,3,1 + 10,6,4,2 oraz 10,7,3,2 + 10,6,5,1 (dlatego ponieważ inne czwórki zawierają te same liczby) wtedy w którymś z kolejnych kółek musimy wstawić 9. Jest to możliwe tylko na 1 sposób ponieważ inne czwórki z 9 zawierają 2 liczby z jednej czwórki. Jednak gdy wstawimy 10,7,3,2 oraz 10,6,5,1 oraz 9,6,4,3 to zostaje nam do wstawienia 8 co nie jest możliwe bo nie ma czwórki z 8 która by pasowała.
Przeciwnie – i pomysłowo, i krótko. Można inaczej, ale chyba nie krócej.
Gratuluję!
mp