Trasa z rygorami

1 grudnia 2011
Marek Penszko

Wędrowanie królem po szachownicy jest łatwe i niezbyt ciekawe – w przeciwieństwie np. do obskakiwania jej konikiem. Trywialną trasę królewskiej wędrówki można jednak przerobić na „przyrząd” do gimnastyki szarych komórek. Jest nim łamigłówka hidato z poprzedniego wpisu, polegająca na odtwarzaniu takiej trasy na podstawie ujawnionych numerów niektórych kolejno zaliczanych pól. Co prawda taka zabawa, jak wiele podobnych, może się łatwo przejeść, ale jeśli ktoś lubi łamać głowę, a nie tylko zabijać czas, to zwykle z przyjemnością zmaga się z trudniejszymi lub niesztampowymi jej wariantami.

Oficjalnie twórcą hidato jest izraelski informatyk Gyora Benedek, który zaczął lansować swój pomysł w 2007 roku. Bardzo podobne zadania pojawiały się jednak znacznie wcześniej, więc choć „plagiat” był zapewne przypadkowy, to wątpliwości nie budzi tylko to, że pan Benedek wymyślił nazwę, którą zresztą zastrzegł. Sytuacja prawna w tej dziedzinie jest dziwna, bo pomysłu zastrzec nie można, więc dwie inne przedsiębiorcze osoby bez przeszkód próbują komercjalizować taką samą łamigłówkę, nazywając ją inaczej – hidoku i numbrix.

Nie najstarsze, ale ciekawe i oryginalne „hidato” pojawiło się na łamach Scientific American w kwietniu 1977 roku – oczywiście w rubryce Mathematical Games Martina Gardnera:

Ujawniono numery tylko czterech pól trasy. Diagram jest wprawdzie mały, ale rozwiązań byłoby mnóstwo, gdyby nie dwa dodatkowe warunki:
1) w każdym kroku kierunek trasy powinien się zmieniać,
2) ukośne fragmenty trasy powinny przecinać się jak najmniej razy.

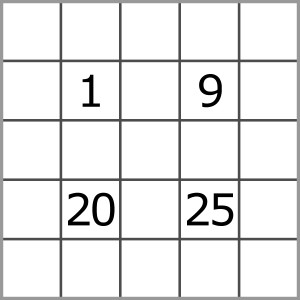
Gwoli jasności poniżej znajduje się rozwiązanie podobnego zadania na mniejszym diagramie; ukośne odcinki przecinają się trzykrotnie (mniej się nie da):

W rozwiązaniu wystarczy podać, jakie liczby znajdą się w rogach i w środku diagramu.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.