Liczebniki
Wiele lat temu w angielskim miesięczniku Games & Puzzles ukazało się następujące zadanie:
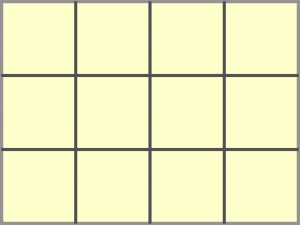
Do 12 pól prostokątnego diagramu 3×4 należy wpisać 12 liter (E F H I N O R T U V W Z) tak, aby poruszając się ruchem króla szachowego, można było odczytać jednym ciągiem liczebniki: ZERO, ONE, TWO, THREE, FOUR, FIVE.
Inaczej mówiąc, każda następna litera powinna być na polu sąsiadującym bokiem lub rogiem z polem z poprzednią literą. Dwie kolejne takie same litery (np. O „na przełomie” ZERO i ONE lub E w THREE) można zaliczać na tym samym polu. Tego rodzaju zadania znane są od dawna, gościły już także kiedyś w Łamiblogu.
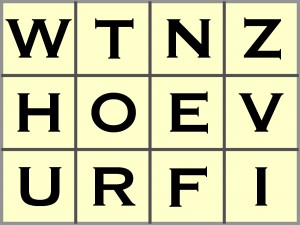
Rozwiązanie autorskie angielskiego zadania wyglądało tak:
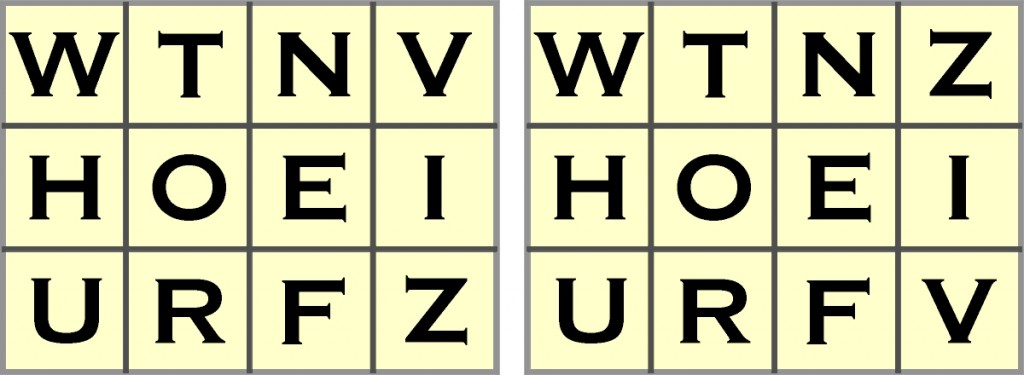
Czytelnicy nadesłali jeszcze dwa nieco inne:
Trudno oprzeć się pokusie spolszczenia pomysłu. Z takim samym zestawem polskich liczebników nie sposób się jednak zmieścić w diagramie 3×4. Ograniczenie liczby liczebników wydaje się ciekawsze niż zwiększanie diagramu, zwłaszcza że od ZERO do CZTERY liter będzie dokładnie 12 (A C D E J N O R T W Y Z; po ZERO jest oczywiście JEDEN, a nie RAZ).
Pytania są trzy:
– czy istnieje rozwiązanie?
– ile jest całkowicie różnych (z dokładnością do obrotów i odbić lustrzanych) rozwiązań, jeżeli jest ich więcej niż jedno?
– jeśli nie ma żadnego rozwiązania, to dlaczego?
Polska wersja zadania wydaje się nieco trudniejsza, bo choć liczebników jest mniej, to polski ciąg liter – a właściwie kroków, czyli ruchów królem – (ZEROJEDENDWATRZYCZTERY) jest dłuższy o jedną literę od angielskiego (ZERONETWOTHREFOURFIVE).
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze
Znam odpowiedź na dwa z trzech pytań.
Rozwiązanie istnieje, tym samym trzecie pytanie jest bezprzedmiotowe (ładnie napisane prawda?).
OJND
CREW
YZTA
DWA
NET
JRZ
OYC
P.S. Zadanie poszło w ciągu minutki, ale juz dalej nie brnąłem i nie szukałem dalszych rozwiązań.
NDJO
WERY
ATZC
C mozna zamienic z Y, a N z D, co daje cztery rozwiazania.
Dlaczego nie wiecej?
1. E ze wzgledu na ilosc sasiadow musi zajmowac jedno ze srodkowych pol.
2. R, T i Z sasiadujace z E nie moga zajmowac rogow planszy (powod – jak wyzej).
3. Analizujac wspolnych sasiadow mozna zbudowac klocki ktore musza znalezc sie w rozwiazaniu:
CY NE ER RY
Z D TZ Z
Liczy sie ksztalt (klocki mozna obracac) i litery ktore skladaja sie na klocki (litery mozna przestawiac).
4. Po zlozeniu tego wszystkiego do kupy pozostaja dwie mozliwosci uplasowania R i Z:
**** ****
*ERY *EZY
*TZC *TRC
5. Z w drugim srodkowym polu odpada bo R musi ‚miec wyjscie’ na O.
6. Dalej idzie jak po sznurku.
Bardzo smaczne 🙂
OJND
CREW
YZTA
i jest to jedyne rozwiązanie (E i R muszą być blisko wielu liter, muszą więc zajmować dwa środkowe pola, a potem jakoś idzie)
Zagadka ta przypomniała mi 12. zadanie eliminacyjne z VI Pucharu Polski (http://sfinks.org.pl/files/puchar2009/puchar2009_eliminacje.pdf)
Znalazłem 4 rozwiązania.
1)
DNJO
WERY
ATZC
2)
DNJO
WERC
ATZY
3)
NDJO
WERC
ATZY
4)
NDJO
WERY
ATZC