Trudno nierówno

21 września 2011
Marek Penszko

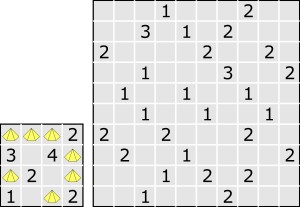
Pierwszym zadaniem w tym wpisie są skarby „1-2”, czyli:
Cyfra w danym polu oznacza, ile skarbów znajduje się w sąsiednich kratkach – stykających się z polem z cyfrą bokiem lub rogiem. W jednej kratce mogą znajdować się jeden lub dwa skarby. W polach z cyframi skarbów nie ma. Należy oznaczyć wszystkie skarby.

Drugie zadanie to skarby „1”, czyli klasyka. Instrukcja jest taka, jak wyżej, poza jednym wyjątkiem: w jednej kratce zawsze jest tylko jeden skarb. I dodatkowa informacja, by rozwiązanie było jedno: wszystkich skarbów jest 20.

Przed zadaniami znajdują się, gwoli jasności, małe przykłady.

Pierwsze zadanie jest najtrudniejszym tego rodzaju („1-2„), jakie zostało dotąd opublikowane. Łatwo było je odszukać, bo takie łamigłówki zamieszczane są regularnie tylko w tureckim piśmie Akil oyunlari, a wszystkich ukazało się dotąd około 20. Drugie to jedno z najtrudniejszych klasycznych skarbów, jakie wyszperałem w archiwum. Pochodzi z działu eksperckiego japońskiego miesięcznika Puzzler.

Teza, którą zamierzałem udowodnić, zamieszczając oba zadania razem, brzmi:
najtrudniejsze skarby „1-2” są trudniejsze niż najtrudniejsze skarby „1”.
Niestety, szybko zauważyłem, że to się nie uda. Wręcz przeciwnie. Ci z Państwa, którzy wezmą się za rozgryzanie obu orzechów, zauważą, że klasyka stawia większy opór. Podstawowa przyczyna tej różnicy jest prosta: nic nie ujmując autorowi tureckiego zadania, skarby „1-2” są dziełem amatora, skarby „1” wyszły spod ręki profesjonalisty, wspomagającego się komputerem. Amator tworzył niczym Matejko, po kawałeczku, bardzo uważając, aby zawsze dało się wnioskować jak po sznurku. Profesjonalista panował równocześnie i nad całością, i nad fragmentami, balansując na granicy logiki i metody prób i błędów oraz dbając o formę (symetryczne rozmieszczenie cyfr). Tę różnicę można zauważyć już na początku rozwiązywania. Tureckie zadanie da się nadgryźć na kilka sposobów w różnych miejscach, natomiast ze znalezieniem punktu zaczepienia w japońskim jest niezły zgryz. Taki punkt startu, w którym wystarczy rozpatrzyć minimum alternatyw, nie uciekając się do próbowania i błądzenia – jest jeden.

W rozwiązaniu pierwszego zadania wystarczy podać, ile jest wszystkich skarbów; w rozwiązaniu drugiego – liczbę skarbów na przekątnych diagramu.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.