Supasu
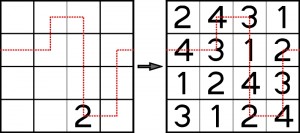
Sudoku, futoshiki, kenken, kropki, strimko, blokowisko – to nazwy najpopularniejszych rodzajów łamigłówek opartych na kwadracie łacińskim, które gościły w Łamiblogu. Rozwiązanie każdej z nich może wyglądać identycznie, np. tak:
1 2 3 4 5
3 1 2 5 4
2 5 4 1 3
5 4 1 3 2
4 3 5 2 1
Inny jest natomiast w każdym przypadku klucz do rozwiązania, czyli dodatkowe relacje między cyframi, które powinny być spełnione, a więc odmienny jest także sposób rozwiązywania.
Całkiem różnych kluczy wymyślono dotychczas kilkanaście (nie całkiem różnych koło setki), choć większość z nich jest mało używana, czyli „otwierane” nimi zadania pojawiają się sporadycznie w specjalistycznych pisemkach. Kilka z tych mniej znanych prezentowałem w Łamiblogu. Dorzucę jeszcze jedno, na które trafiłem ostatnio, przeglądając japoński magazyn Puzzler.
Łamigłówka nazywa się supasu, czyli cyfrowa ścieżka. Oto mały przykład z rozwiązaniem:
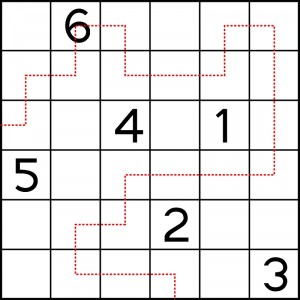
Nie podam jednak, jaki jest klucz do rozwiązania. Postanowiłem powrócić do dawno nie widzianych w Łamiblogu indugadek. Inaczej mówiąc, chodzi o rozszyfrowanie zasad łamigłówki na podstawie przykładu. Zachęcam – nie bez wahania – do indukowania, bo choć zasada do odgadnięcia jest prosta (jedno krótkie zdanie), to wpadnięcie na nią niekoniecznie. Może będzie łatwiej, jeśli dorzucę jeszcze jeden, nieco większy przykład i z większą liczbą su podanych na początku, w tym dwóch na pasu:
A na koniec orzeszek do rozgryzienia jako nagroda dla tych, którzy okażą się dobrymi induktorami:
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
Na ścieżce ma się znależć:
– jedna jedynka,
– dwie dwójki,
– trzy trójki,
– cztery czwórki
itd. aż do zapełnienia całej ścieżki.
Pozdrawiam
263154
431562
624315
512436
356241
145623
Już mi się wydawało, że znalazłam zasadę, która jest dość prosta i pasuje do przykładów, ale według niej nie da się rozwiązać zadania 🙁
Oto ona:
We wszystkich pionach pozostały niewykreślone liczby które są mniejsze bądź równe liczbie niewykreślonych liczb.
Czyli np.: w pierwszym przykładzie w pierwszym pionie jest niewykreślonych 3 liczby, więc są to 1, 2 oraz 3. (Czwórka jest skreślona, bo jest większa od 3).
Według tej zasady da się równoznacznie rozwiązać dwa przykłady, jednak nie da się rozwiązać zadania 🙂
No cóż, będę myślała dalej.
Hm…, na to bym nie wpadł. Chyba ciut zbyt zakręcone.
mp
263154
431562
624315
512436
356241
145623
Na ścieżce musiały wystąpić cyfry: 1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,6,6,6,6,6.
Udało mi się (chyba):
Skreślonych jest tyle jednakowych liczb jaka jest ich wartość (czyli jedna jedynka, dwie dwójki, itd).
Rozwiązanie:
263154
431562
624315
512436
356241
145623
Witam,
W podanych ciągach musi się znaleść jedna cyfra 1, dwie cyfry 2, trzy cyfry 3, itd…
rozwiązanie wierszami:
263154
431562
624315
512436
356241
145623
i Pozdrawiam
zasada: w częśc ściezki z danego rzędu kwadratu łacińskiego wpisujemy największe cyfry (poza ujawnionymi)
263154
431562
624315
512436
356241
145623
pzdr
ha, do mojego rozwiązania nie pasuje drugi przykład:)
Ha, nie ujawniam od razu rozwiązania, bo – o dziwo – choć zasada jest zła, to rozwiązanie jest dobre.
mp
Wydaje mi się, że suma wszystkich su znajdujących się na pasu jest sumą szeregu n^2 gdzie n = 1 do 4 w pierwszym przykładzie (30), do 5 w drugim (55) oraz 6 w zadaniu (91)
1^2+2^2+3^2+4^2+5^2+6^2 = 91
czyli na pasu musi się znaleźć 6 szóstek, 5 piątek, itd. Trochę kreślenia i zmazywania dało mi poniższy kwadrat. Mam nadzieje, że dobrze przepisałem…
2 6 3 1 5 4
4 3 1 5 6 2
6 2 4 3 1 5
5 1 2 4 3 6
3 5 6 2 4 1
1 4 5 6 2 3
Pozdrawiam 🙂
Odpowiednio odczytane równanie:
n(n+1)/2=1+2+3+…,
gdzie n-długość boku diagramu (kwadratu),
może być wskazówką do umieszczenia liczb na „pasu”.
263154
431562
624315
512436
356241
145623
Na „pasu” pojawiaja sie cyfry od 1 do n (gdzie n=bok kwadratu), przy czym cyfra n pojawic sie musi n razy (jedna jedynka, dwie dwójki, trzy trójki … itd)
Warunek okazał się być dość latwy do wykrycia, a samo zadanie jeszcze łatwiejsze …
Jak dla mnie – dość łatwe.
Na linii mają być: 1 jedynka, 2 dwójki, 3 trójki, itd.
Rozwiązanie zadania:
263154
431562
624315
512436
356241
145623
Na nitkę należy nawlec jedną 1, dwie 2, trzy 3, …, sześć 6. Pozdrawiam 🙂
nie było zbyt trudne:
263154
431562
624315
512436
356241
145623
zasada jest taka:
na linii jest po n liczb n (jedna jedynka, dwie dwójki, …, sześć szóstek)
lub:* suma liczb na linii jest równa:
Sum(i (1,N)) i^2, gdzie N jest wielkością kwadratu
*co do drugiej zasady to nie jestem pewny 😉
263154
431562
624315
512436
356241
145623
W kwadracie o boku n każda liczba od 1 do n występuje na linii przerywanej tyle razy ile wynosi jej wartość.
Pozdrawiam
263154
431562
624315
512436
356241
145623
Każda cyfra wystepuje na sciezce tyle razy, jaka jest jej wartosc.
a
263154
431562
624315
512436
356241
145623
263154
431562
624315
512436
356241
145623
Na linii musi być jedna jedynka, dwie dwójki,…, sześć szóstek.
Zaintrygowana sformułowaniem „jedno krótkie zdanie” postanowiłam ograniczyć słowa do minimum.
Wychodzi mi, że potrzeba sześciu słów, a mianowicie:
„n występuje na linii n razy”.
Krócej się chyba nie da?
Pozdrawiam
mw
Każda cyfra powinna być na drodze swoją ilość razy (użyłem wyrazu „swoją”, by zdanie było rzeczywiście krótkie)
Poruszyło mnie słowo INDUGADKI. Doskonałe! Prawie jak „indugatki”… choć nie wiem, co to mogłoby być…
Wracając do zadania – tak sobie myślę ironicznie i szyderczo, iż nieszczęsny czytelnik nie dość, że zadanie ma rozwiązać, to jeszcze musi wymyślić sobie jego treść! No wie Pan? Takie rzeczy ?! Idzie Pan na łatwiznę! 🙂 Niedługo będzie trzeba wymyślać jeszcze nazwy zadań. Sam sobie zrób zagadkę i sam sobie ją rozwiąż, a ja w tym czasie zajmę się czymś innym. :))
A tak trochę bardziej na poważnie:
Intryguje mnie, czy udało się Panu stworzyć kiedyś zagadkę, której nie umiał Pan rozwiązać. Rozwiązywalną zagadkę rzecz jasna. Taką, którą rozwiązałby być może ktoś inny.
Jeśli nie – to oto ja – skromy czytelnik, mam właśnie taką zagadkę dla Pana. Czy Bóg może stworzyć kamień, którego nie będzie mógł podnieść? Filozoficznie się zrobiło…
Pozdrawiam bardzo serdecznie.
Jest mnóstwo nierozwiązanych problemów matematycznych.
Zdarza się, że mam spore kłopoty z rozwiązaniem jakiejś dawnej zagadki własnego autorstwa, do której przymierzam się po kilku latach. Natomiast taką „radykalną” sytuację, o jaką Dalaj Lama pyta, przypominam sobie tylko w kulinarnym kontekście: upitrasiłem kiedyś potrawę, której nie byłem w stanie zjeść, natomiast zjadł ją z apetytem pies sąsiada (i przeżył).
Boskich kwestii nie będę wałkował, bo to znany paradoks http://pl.wikipedia.org/wiki/Paradoks_omnipotencji
mp
I jeszcze jedno. Spieszę skonstatować, iż nad Pana wizerunkiem u góry strony kąpie się dziś jakaś na wpół naga kobieta zachęcając tym samym do wjazdów w tropiki. Miło się zrobiło. Tylko na zadaniu skupić się nieco trudniej.