Nieprostą drogą

9 stycznia 2011
Marek Penszko

Układanie zadania może być plątaniem prostej drogi. Rozwiązywanie – odwrotnie.
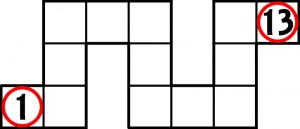
Prosta droga wygląda np. tak:

Należy dotrzeć od jedynki do trzynastki, wpisując w zaliczane pola kolejne liczby. Z pola na pole można przechodzić także na ukos.
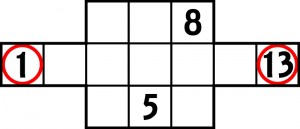
Siedząc przy piwku z góralem, który ma smykałkę do zagadek, zastanawialiśmy się, ile by trzeba wypić, aby mieć kłopot z rozwiązaniem tego „zadania”. Góral stwierdził, że w tym lokalu nie ma tyle alkoholu. Nie sprawdzaliśmy, czy o słuszności tego stwierdzenia zadecydowałoby słabe zaopatrzenie, czy mocna głowa. Spróbowiliśmy natomiast nieco poplątać drogę. Efekt był taki:

Zasady zabawy są identyczne, a niektóre „przejściowe” liczby są już ujawnione. To oczywiste, że teraz jest łamigłówka, bo trzeba pokombinować i pogłówkować, ale tylko odrobinę.

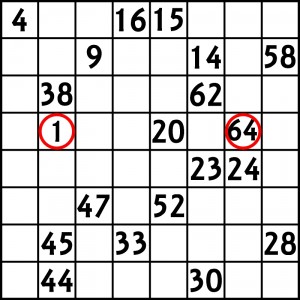
Przed 4 laty pewien izraelski matematyk w ramach mody posudokowej rozwinął powyższy pomysł plątania drogi i próbował pójść śladem Wayne’a Goulda, czyli zarobić na miłośnikach rozrywek umysłowych. Włączyło się w to kilka amerykańskich i angielskich gazet (m. in. USA Today i Daily Mail), publikując łamigłówki w rodzaju takich, jak powyższa, ale oczywiście trudniejsze, czyli mniej więcej takie, jak poniższa:

Wprawdzie świata toto nie podbiło, ale do w miarę pożytecznego zabijania czasu nadaje się równie dobrze jak sudoku i też jest matematycznie ciekawe (wyznaczanie ścieżki Hamiltona w grafie króla szachowego).
W rozwiązaniu wystarczy podać 15 liczb: na przekątnej łączącej lewy górny róg z prawym dolnym (zaczynając od ujawnionej czwórki) oraz w dolnym rzędzie z ujawnionymi 44 i 30.

I pytanie dodatkowe: kto znał tę łamigłówkę wcześniej i wie, jak się nazywa (nazwy są przynajmniej dwie)?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.