Sudoku z wiesiołkiem
W sezonie ogórkowym powracają kuriozalne tematy. Dawniej był to potwór z Loch Ness, dziś powraca… „potworne” sudoku.
Daily Mail odgrzał informację sprzed czterech lat o najtrudniejszym na świecie sudoku, którą podchwyciły media, np. Onet.pl. Główny bohater jest ten sam, fiński matematyk Arto Inkala z Politechniki Helsińskiej, natomiast inne jest jakoby najtrudniejsze zadanie i specyficzne są okoliczności, w jakich się pojawiło.
Fin, specjalista od matematyki stosowanej, szerzej znany jest z wydanego w 2006 roku zbiorku zadań, zawierającego m. in. sudoku, które uznano wówczas za najtrudniejsze na świecie. Miało nawet nazwę – AI Escargot. AI to inicjały autora, Escargot – po francusku ślimak. To drugi ślimak, bo pierwszy powstał rok wcześniej – nie był jeszcze francuski, tylko fiński (Etana), ale oczywiście także się ślimaczył, czyli rozwiązywało się go bardzo długo, jeżeli komuś w ogóle starczało cierpliwości, by dobrnąć do końca.
Tym razem zaczęło się od firmy Efamol, znanej z leku o takiej samej nazwie, wytwarzanego z nasion wiesiołka. Lek uchodzi za niemal panaceum. Firma zamówiła u matematyka trzeciego ślimaka dla uczczenia… dobroczynnego wpływu na umysł kwasów tłuszczowych omega-3. Zapewne chodziło też o coś w rodzaju reklamy: „nie możesz rozwiązać tego zadania? – zażywaj nasze medykamenty, a na pewno sobie poradzisz”.
Warto wyjaśnić, że fiński matematyk od początku traktuje sudoku jako pole doświadczalne do badań nad algorytmami; szczególnie interesują go tzw. algorytmy genetyczne. Najtwardsze plony z tego pola przeznaczone są raczej dla komputerów, niż dla ludzi, chyba że ktoś lubi ślęczeć nad rozwiązaniem, ćwicząc na przykład upór.
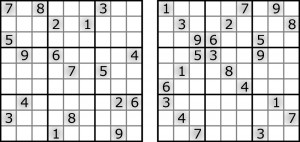
Trzeci ślimak pełznie na podanych wyżej stronach Daily Mail i Efamolu. Pierwszy i drugi poniżej.
Aby zrozumieć, dlaczego wszystkie ślimaki określane są jako najtrudniejsze sudoku, proponuję zabawę, polegającą na rozwiązywaniu zadań etapami za pomocą metodycznego solvera Stuarta. Przedtem nie zaszkodzi przekonać się, że rozwiązując na piechotę, ale logicznie, w każdym przypadku wpiszemy do diagramu nie więcej niż dwie cyfry. Wspomniany solver jeszcze to i owo wyeliminuje, korzystając z ekstremalnych metod, ale więcej cyfr nie wpisze tylko… podda się. To bardzo rzadki przypadek, aby stosujący logiczne metody program komputerowy nie poradził sobie z sudoku. Ślimaki są więc najtrudniejsze nie z punktu widzenia – że tak powiem – ludzkiej logiki, tylko komputerowej. Wprawdzie w obu przypadkach logika (sposób wnioskowania) jest taka sama, ale by znaleźć miejsce, w którym należy skorzystać z jakiejś zawiłej metody oraz ustalić z jakiej, potrzebne są komputerowa spostrzegawczość i cierpliwość. Gdy logiczna metoda, którą wypada zastosować, jest diaboliczna lub ekstremalna, człowiek albo da sobie spokój, albo zdecyduje się na próbowanie i błądzenie, bo to prostszy, pewniejszy i zwykle szybszy sposób dotarcia do celu. Gdy natomiast, jak w przypadku ślimaków, logika zawodzi, wówczas i człowiek, i komputer skazani są na metodę prób i błędów. Człowiek jest niestety ślimakiem, natomiast solvery, stosujące np. backtracking, podają rozwiązanie w ułamku sekundy.
Dla odmiany proponuję w pełni i po ludzku logiczną zabawę z krewniakiem sudoku.
W puste pola należy wpisać takie liczby, aby w każdym rzędzie i w każdej kolumnie występowały różne, ale kolejne (tworzące, po ustawieniu od najmniejszej do największej, fragment ciągu liczb naturalnych).
Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.


Komentarze
Czy 0 to liczba naturalna?
Istotnie, wypadałoby sie umówić, bo nie ma jednoznacznej odpowiedzi.
Zakładałem, że nie. Nawet nie wiem, czy z zerem naturalnym zadanie ma rozwiązanie.
m
PS Rzuciłem szybko okiem i jakoś nie widzę miejsca, gdzie możnaby wstawić zero
1 3 6 X 2 7 4 5
X 6 X 5 8 4 7 3
5 7 8 9 X 6 X 4
X 8 9 6 7 X 10 X
3 X X 7 4 5 8 6
4 5 10 8 6 X 9 7
2 4 X X 5 3 6 1
6 9 7 4 3 8 5 2
Akurat się tak szczęśliwie złożyło, że rozwiązania z zerem nie ma. A rozwiązanie bez zera prezentuje się następująco (mam nadzieję, że niczego nie pokręciłem):
1 3 6 x 2 7 4 5
x 6 x 5 8 4 7 3
5 7 8 9 x 6 x 4
x 8 9 6 7 x 10x
3 x x 7 4 5 8 6
4 5 10 8 6x 9 7
2 4 x x 5 3 6 1
6 9 7 4 3 8 5 2
gdzie x oznacza czarne pole.
136 2745
6 58473
5789 6 4
8967 A
3 74586
45A86 97
24 5361
69743852
A=10, żeby równo wyszło 🙂
Oops! I tak, nie wyszło równo 🙁 Jeszcze raz.
136X2745
X6X58473
5789X6X4
X8967XAX
3XX74586
45A86X97
24XX5361
69743852
136.2745
.6.58473
5789.6.4
.8967.0.
3..74586
45086.97
24..5361
69743852
Gdzie zero to 10. (Ale i tak pewnie komentarz się rozjedzie :))
MATKO BOSKA jak takie sudoku się układa?
A co do zadania:
1362745
658473
578964
8967 10
374586
45 10 8697
245361
69743852
1,3,6-2,7,4,5
-6-5,8,4,7,3
5,7,8,9-6-4
-8,9,6,7-10-
3–7,4,5,8,6
4,5,10,8,6-9,7
2,4–5,3,6,1
6,9,7,4,3,8,5,2
1-3-6-X-2-7-4-5
X-6-X-5-8-4-7-3
5-7-8-9-X-6-X-4
X-8-9-6-7-X-0-X
3-X-X-7-4-5-8-6
4-5-0-8-6-X-9-7
2-4-X-X-5-3-6-1
6-9-7-4-3-8-5-2
X = czarne pole
0 = 10
a
136_2745
_6_58473
5789_6_4
_8967_0_
3__74586
45086_97
24__5361
69743852
(0 znaczy 10)
pozdrawiam
Michał
136X2745
X6X58473
5789X6X4
X8967X10X
3XX74586
451086X97
24XX5361
69743852
Drugi ślimak ma 308 rozwiązań. Ale to dlatego, że brakuje jednej cyfry. W ostatniej kolumnie w 5 wierszu powinna być 2. I wtedy jest oczywiście jedno rozwiązanie