26 stawów

29 czerwca 2010
Marek Penszko

Nurikabe jest łamigłówką binarną, bo w każdej kratce diagramu możliwe są dwa stany – albo jest czarna albo biała. Diagram z rozwiązaniem odpowiada macierzy binarnej, w której jedynki zastąpiono czarnymi kratkami, a zera białymi. Przypomina do złudzenia niektóre tzw. kody dwuwymiarowe.
Ta własność jest podstawą wszystkich sposobów rozwiązywania. Po prostu: jeśli ustalimy, że pole nie może być białe, to musi być czarne – i odwrotnie. Stąd już tylko krok do szkółki rozwiązywania, ale w Łamiblogu szkółek nie ma. Po pierwsze dlatego, że większość uczniów przerasta nauczyciela, a jeśli przypadkiem tak nie jest, to po drugie – nie ośmieliłbym się zabierać nikomu przyjemności samodzielnego przecierania szlaków wiodących do celu. A po trzecie – szkółki są zwykle nudnawym mądrzeniem się i mało kto je czyta. Warto natomiast pochwalić się odkryciem jakiegoś oryginalnego sposobu rozwiązywania.

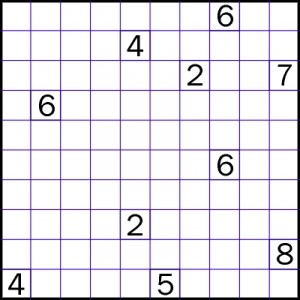
Nurikabe przez kilka lat pozostawało zadaniem firmowym wydawnictwa Nikoli i nie było znane poza Japonią. Dopiero w roku 1998 konkurencja uprowadziła je za granicę i pojawiło się pod nazwą Lay bricks (ułóż cegły) na 7. Łamigłówkowych Mistrzostwach Świata, a potem na kilku następnych. Szerzej stało się znane na fali posudokowej mody na główkowanie po japońsku. Dziś stron z tą łamigłówką w sieci jest tyle, że prezentowanie zwykłych zadań w Łamiblogu wydaje się tak nieoryginalne, że aż deprymujące. Mam jednak nadzieję, że poniższe propozycje są choć trochę niezwykłe, ponieważ pochodzą ze wspomnianych mistrzostw świata – pierwsze ze Stambułu (1998), drugie ze Stamfordu (2000). Które z nich jest twardszym orzechem? Pytanie retoryczne – wystarczy spojrzeć na diagramy.

W każdym rozwiązaniu wystarczy podać, ile czarnych kratek, tworzących groblę, jest w sumie na przekątnych i przy brzegach diagramu.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.