My, blokersi

8 czerwca 2010
Marek Penszko

Błądzę ostatnio po blokowiskach, czyli wśród wieżowców, ale nie sam. Co ciekawe, mój towarzysz wędrówki ma oryginalny pogląd na kluczowe informacje ujawniane w tych zadaniach. Zanim jednak ów pogląd przedstawię, przypomnę, na czym polega błądzenie, bo może zajrzy tu nowy kandydat na łamacza głowy.

Prostopadłościennych bloków jest n^2 i są one ustawione w kwadrat n x n. Każdy blok to albo sześcian, albo słupek z sześcianów – ich liczba określa wysokość bloku. W każdym rzędzie i w każdej kolumnie stoi n bloków o różnych wysokościach – od 1 do n.
Dla n = 4 blokowisko może wyglądać np. tak:

Jeśli na dachu każdego domu napisać liczbę oznaczającą jego wysokość i spojrzeć z lotu ptaka-matematyka na całą zabudowę, to pojawi się kwadrat łaciński:

W roku 1992 pewien nauczyciel matematyki z Osaki wpadł na pomysł przerobienia tego widoku-kwadratu na ćwiczenie gimnastykujące umysł. Najpierw umieścił 4n cyfr ze strzałkami wokół blokowiska:

Każda cyfra przy brzegu oznacza, ile bloków widzi ptak „zawieszony” w miejscu tej cyfry – mniej więcej na wysokości n/2 – wpatrzony, zgodnie ze wskazaniem strzałki, w rząd (kolumnę) bloków, przed którą się znajduje.
Teraz wystarczy oczyścić wszystkie dachy i usunąć większość cyfr ze strzałkami (oczywiście nie byle które) – i łamigłówka gotowa:

Celem jest oczywiście wypełnienie diagramu cyframi, czyli określenie, wysokości każdego bloku.

Warto dodać, że z matematycznego punktu widzenia każdy rząd bloków odpowiada permutacji ciągu cyfr od 1 do n, a cyfra przy brzegu określa długość najdłuższego podciągu rosnącego w tej permutacji, zaczynającego się (pierwszy wyraz) od brzegu. Takie ujęcie dodaje prestiżu „frywolnej” łamigłówce, bowiem podciągi w permutacjach są tematem poważnych dysertacji.

Nauczyciel nazwał zadanie budowaniem miasta. Po mojemu (i nie tylko) to blokowisko; często pojawiają się też wieżowce (skyscrapers – najbardziej przewrotne, bo najwyższe wieżowce są kilkupiętrowe), a czasem inne obcojęzyczne określenia, np. urban panorama, flats lub towers.

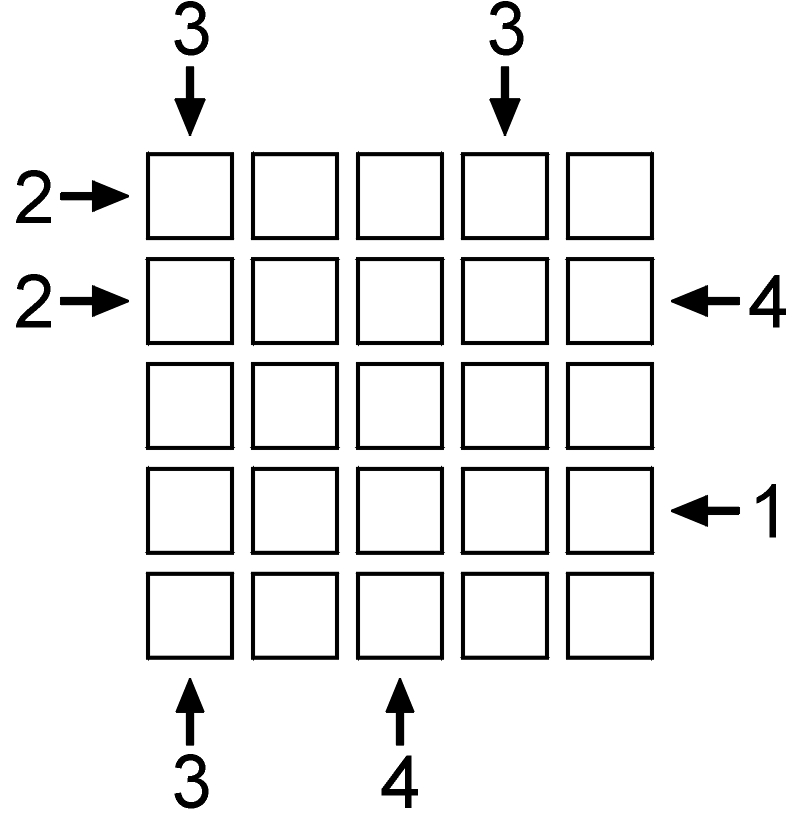
Świeżo upieczonym blokersom proponuję na dzień dobry niełatwą wprawkę z pięciopiętrowymi drapaczami chmur:

A teraz wracam do zapowiedzianego na początku oryginalnego poglądu mojego towarzysza wędrówki po blokowiskach. Otóż jest on zwolennikiem umieszczania przy brzegu wszystkich 4n cyfr, a nie tylko niektórych wybranych. Twierdzi (cytuję):

…za bardzo nie przepadam za zadaniami, gdzie ujawnionych jest tylko tyle cyfr, ile potrzeba, bo rozwiązujący wtedy wie, z czego korzystać, dlatego uznaję to za ułatwienie, a jeśli ujawnione są wszystkie – wtedy dodatkowo musi szukać w gąszczu tych, które naprawdę się przydadzą.

Stwierdzenie, że mniej informacji to ułatwienie, może się wydać dziwne. Z drugiej jednak strony wyjaśnienie, dlaczego tak jest, brzmi całkiem sensownie. Być może ktoś z Państwa chciałby podzielić się własnym zdaniem na ten temat. Dodam dla zachęty, że autorem kontrowersyjnej opinii jest nie byle kto – dwukrotny mistrz świata w rozwiązywaniu sudoku i równie tęga głowa do innych zadań.

Nie sprawdzałem, czy poniższe blokowisko może być przykładem na poparcie którejś opcji, proponuję więc rozwiązać je, następnie wpisać wszystkie cyfry wokół pustego diagramu i po 24 godzinach… zapomnieć i rozwiązać jeszcze raz. Jak pójdzie – łatwiej, czy trudniej?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.