Wolne bandy

24 listopada 2009
Marek Penszko

Dziękuję Państwu za uwagi dotyczące sposobu rozwiązywania „obchodów” zamieszczonych w poprzednim wpisie. Na wyróżnienie zasługuje zwłaszcza Jazza obrona logiki – mimo „zdecydowanego tonu”:). Trudno się nie zgodzić z opisanym w komentarzu Jazza sposobem wnioskowania o przebiegu trasy, ale warto zauważyć, że jest on skuteczny tylko do pewnego momentu („musimy tylko ustalić…”; „nie wiemy tylko jeszcze…”) i w szczególnych okolicznościach („jeśli dwa przystanki znajdują się przy brzegu planszy…”). Poza tymi sprzyjającymi okolicznościami przydaje się – albo przynajmniej jest efektywniejszy – tzw. „czuj”. Mówiąc ogólnie, najwygodniej próbować naszkicować najpierw orientacyjny przebieg trasy – bez zwracania uwagi na pola diagramu. Trzeba jedynie uważać, by nie iść więcej niż n-krotnie między liczbami przesmykiem, którego szerokość umożliwia tylko n-krotne przejście oraz aby trasa nie rozdzielała na amen kolejnych liczb. O niekrzyżowaniu się linii już nie wspominam, bo to wynika z reguł zadania.
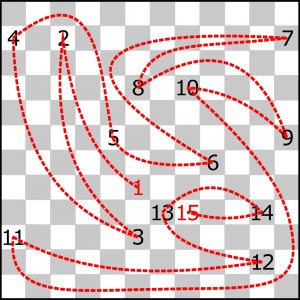
Stosując tę nieprecyzyjną metodę do większego diagramu z poprzedniego wpisu, otrzymalibyśmy coś mniej więcej takiego:

Teraz wystarczy linie ładnie poukładać w kratkach, co nie jest trudne, skoro wiemy, że rozwiązanie jest tylko jedno.
Może się jednak zdarzyć, że układanka nie wyjdzie. Wtedy trzeba próbować coś zmienić w zgrubnej trasie.

Kto często bawi się podobnymi zadaniami (np. number linkiem), ten szybko dochodzi do wprawy, odkrywa pewne typowe triki i rozwiązuje obchody z marszu, od razu rysując łamaną, często zaskakująco szybko. Przykładem może być Pafcio, którego sprint wprawił mnie w osłupienie. Uwolniłem poprzedni wpis, poszedłem na chwilę do kuchni przygotować śniadanie, wracam, a tu pyk! – wskakuje komentarz Pafcia z rozwiązaniami obu zadań, w dodatku z uwagą, że liczenie zakrętów trwało dłużej, niż samo rozwiązywanie. Już nie wspominam o tym, że wpis trzeba przeczytać, a zadania wydrukować. Tym razem Pafciowi należy się szóstka, i to z plusem, nawet jeżeli czyhał na wpis:).

Wracając do komentarza Jazza: podana w nim reguła opiera się na bandach, czyli na liczbach umieszczonych przy brzegach diagramu. Postanowiłem więc sprawić Jazzowi psikusa – oczywiście z pełnym szacunkiem dla rozważań zawartych we wspomnianym komentarzu.
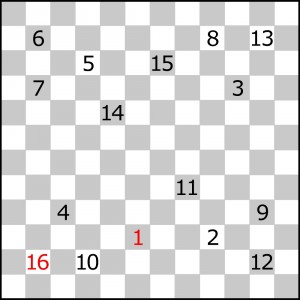
A jeśli przy bandach liczb nie będzie?

Jak teraz nadgryźć skutecznie obchód na logikę? I czy w ogóle warto?

W rozwiązaniu wystarczy jak zwykle podać liczbę załamań trasy.