Same sumy

16 września 2009
Marek Penszko

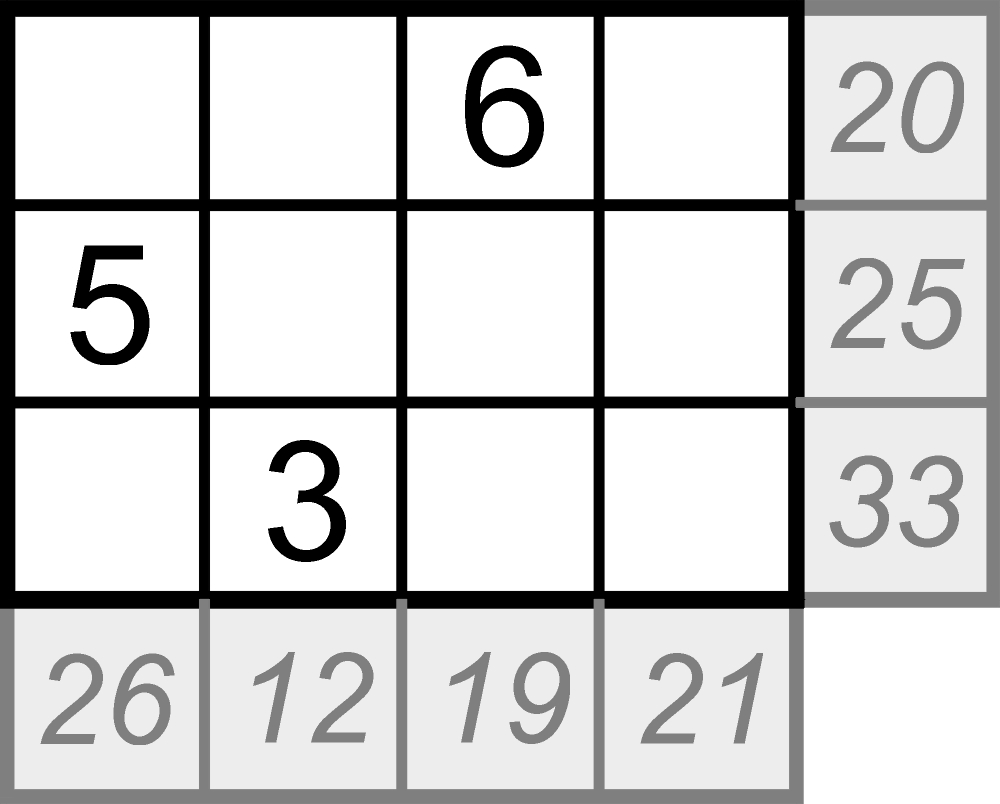
Profesor Seppo Mustonen z Uniwersytetu w Tampere, matematyk zajmujący się głównie statystyką i informatyką, wymyślił przed trzema laty łamigłówki survo. Inspiracją była posudokowa moda na kakuro, co łatwo zauważyć, porównując oba rodzaje zadań. Diagram survo jest prostokątem m x n = k, w pola którego należy wpisać liczby o 1 do k tak, aby sumy liczb w rzędach i kolumnach były równe podanym przy brzegach. Poniżej prosty przykład – w diagramie powinny znaleźć się liczby od 1 do 12; niektóre z nich są już ulokowane gdzie należy. 

 

Łamigłówka przeszła prawie bez echa, pojawiała się tylko niedługo w jednym z fińskich dzienników. I nic dziwnego. Jest nie mniej sztampowa niż kakuro, pod względem atrakcyjności daleko jej do japońskich orzeszków z plantacji Nikoli, a walorami dydaktycznymi (ćwiczenie rachunkowe) nie dorównuje zabawom w rodzaju kenken. Nie jest też oryginalna, bo bardzo podobne zadania pojawiały się od dawna. W gruncie rzeczy kwadrat magiczny to także survo, choć szczególne, bo wszystkie sumy są w nim jednakowe.

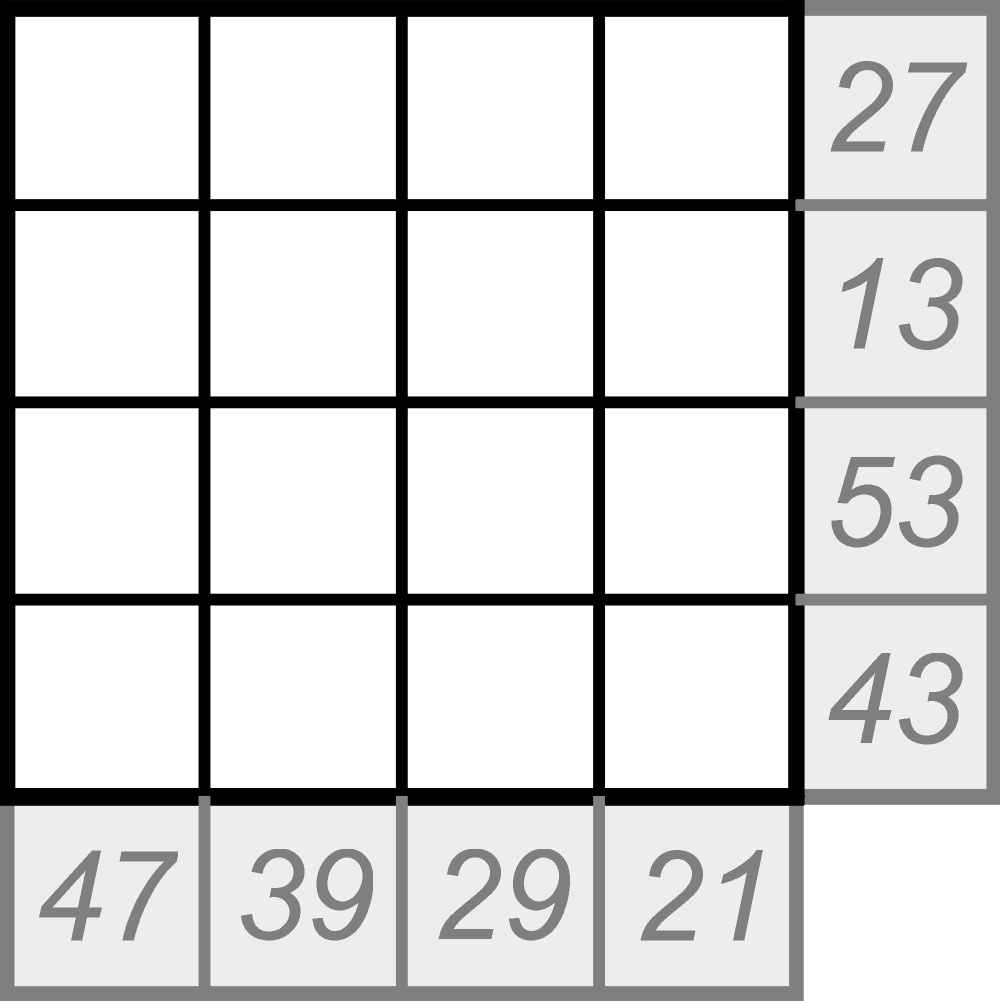
Nie ulega natomiast wątpliwości, że fiński wynalazek jest interesujący jako obiekt matematyczny, czyli tablica prostokątna utworzona z m x n kolejnych liczb naturalnych tworzących m + n sum. Wiąże się z tym kilka ciekawych, dotąd nie rozstrzygniętych problemów algebraicznych. Nie wiadomo na przykład, ile jest różnych czystych (bez ujawnionych na wstępie cyfr-podpowiedzi) diagramów 5 x 5 z podanymi sumami, które mają dokładnie jedno rozwiązanie. Oto przykład takiego „dziewiczego” zadania 4 x 4 z jednym rozwiązaniem – raczej jako ciekawostka, niż do rozwiązywania, chyba że… na własne ryzyko. Jeśli ktoś z Państwa spróbuje się z tym zmierzyć „na piechotę” i dotrze do celu, proszę o informację, ile czasu zajęła droga.

 

Postanowiłem poświęcić parę wpisów protoplastom i kuzynom survo i kakuro, czyli łamigłówkom, w których chodzi o rozszyfrowanie cyfr, gdy sumy niektórych z nich są znane. Najciekawsza w takich dziełkach jest forma, czyli „opakowanie” wspomnianej elementarnej zasady arytmetycznej oraz występujące czasem niuanse merytoryczne.

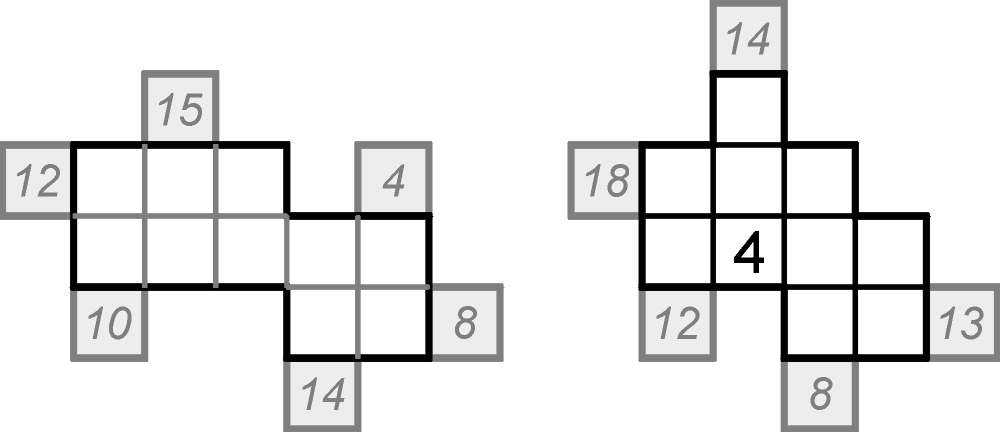
Na początek dwa przykłady drobiazgów lansowanych przez Czechów przed 9 laty.

 

Reguły obu łamigłówek są identyczne. Jakie? – to także zagadka. Bardzo łatwa, skoro temat jest znany, ale z odrobiną podstępu. Warto dodać, że zadania mają po jednym rozwiązaniu.

Zaś tych z Państwa, którzy mieliby ochotę bliżej zapoznać się survo, profesor Mustonen zaprasza na swoją stronę.