Tylko parami

19 sierpnia 2009
Marek Penszko

Łamigłówkom z monetami można by poświęcić odrębny blog. Wiele z nich należy do tzw. rozrywek barowych, którymi przed laty wypełniali czas panowie sączący piwo w pubach. Monety zawsze były pod ręką, a potrzeba zabicia nudy okazała się matką zagadek i sztuczek z ich wykorzystaniem. Powstało tak wiele monecianek, że wydano nawet parę książek-zbiorków, na przykład ten i ten.

Przesuwanki bilonu, do których przyłożyli ręki uczeni, są zwykle nieco trudniejsze i do barowych raczej trudno je zaliczyć – już prędzej do stolikowych kawiarnianych. Goszcząca w dwóch poprzednich wpisach monecianka matematyka holenderskiego Frederika Schuha oparta jest na podobnej łamigłówce opisanej w roku 1884 przez szkockiego fizyka Petera Taita.

Przesuwając w każdym ruchu równolegle (bez obracania) po dwie sąsiednie (stykające się) monety, należy w trzech ruchach zmienić „przeplatankę” w „separatkę”, czyli jak na rysunku – duże na prawo, małe na lewo *** .
Warto zwrócić uwagę, że nie ma tu obowiązującego w zadaniu Schuha warunku, aby przesuwana para była hetero – homo jest równouprawnione.

Ten i dwa poprzednie Łamiblogowe wpisy nie tylko dotyczą jednej grupy łamigłówek, czyli monecianek, ale w dodatku tylko jednego rodzaju zadań z tej grupy – takiego, w którym przesuwa się zawsze równocześnie dwie stykające się monety równolegle, jakby były ze sobą sztywno połączone. Dodatkowym potwierdzeniem wąskiej specjalizacji jest też to, że nawet w ramach tego rodzaju daleko do wyczerpania tematu. Wystarczy zauważyć, że zagadnienie było analizowane po uogólnieniu do n monet małych i n dużych, a nawet do n monet o każdej z k wielkości albo w każdym z k kolorów (w naszych zadaniach ograniczamy się do k = 2). Pojawiały się też nowe „okoliczności” – matematycy rozpatrywali np. sytuacje, gdy przesuwane pary monet można obracać, czyli przesunięcie nie musi być równoległe. Bibliografia dotycząca zadania Taita i wariacji na jego temat liczy ponad 50 pozycji, w tym kilkanaście artykułów w czasopismach naukowych. Zaskakująca jest także informacja podana w Historii matematyki chińskiej Martzloffa, że zadanie to i oczywiście jego rozwiązanie znajduje się w książce wydanej w Chinach w XVII wieku.

Kończąc na razie z monetami, a w szczególności z parami monet, proponuję pogłówkować nad czymś całkiem współczesnym. Autorem zadania jest ukraiński „gołowołomszczik” Serhij Grabarczuk.

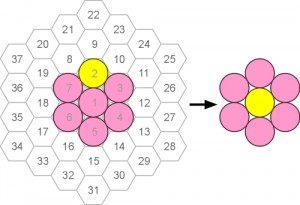
Każdy ruch polega na równoległym przesunięciu pary stykających się kolorowych monet. Po ruchu przesunięta para musi stykać się z grupą pozostałych. Po pierwszym ruchu w każdej chwili w układzie monet musi występować przynajmniej jedna triada (trzy monety, z których każda styka się z dwiema pozostałymi), a w jej skład powinna wchodzić przynajmniej jedna z monet przesuniętych w poprzednim ruchu. Po trzech ruchach żółta moneta stanowiąca dno koszyczka kwiatowego (astra?) powinna znaleźć się na swoim miejscu, czyli w środku.
A gdyby nie było warunku z triadą, czy zadanie byłoby dużo prostsze?

***  – a może odwrotnie?