Winogrona
Wyobrażam sobie, że Ci z Państwa, którzy nadsyłają rozwiązania zadań, stanowią grupę nieoficjalnych przedstawicieli licznego grona rozwiązujących, oddelegowaną do ożywiania Łamibloga, czyli ku pokrzepieniu serca autora. Wielkie dzięki dla wszystkich „chwalących się” rozwiązaniami. Cieszą także dołączane do rozwiązań komentarze – wszystkie, ale zwłaszcza te skłaniające do refleksji lub do rozwinięcia tematu.
Michał napisał, że zadanie z poprzedniego wpisu nie podobało się, bo mało w nim do myślenia, głównie „guess-and-check”. Polemizowałbym, że jednak nie tak mało, a nawet przynajmniej pół na pół, jeśli nie zabierać się zbyt szybko za próbowanie i błądzenie, które wcześniej można elegancko ograniczyć i zaplanować. Wystarczy zauważyć, że do wpisania zostało sześć liczb nieparzystych (N) i sześć parzystych (P), a to pozwala ustalić tylko trzy możliwe schematy rozmieszczenia liczb:
W pierwszym i drugim trzeci rząd jest taki sam, więc oba można sprawdzać w tym samym „podejściu” i dość szybko wyeliminować. Pozostaje krótkie błądzenie w trzecim schemacie; warto przy tym pamiętać, że liczba 15 musi znaleźć się w podstawie trójkąta.
Rozwiązanie jest jedno, a zatem w trójkącie różnicowym piątego rzędu (5-liczbowy bok), czyli utworzonym z liczb od 1 do n = 15, rozmieszczenie liczb jest unikatowe (z dokładnością do symetrii). Dla żadnego n > 15 takiego trójkąta nie sposób utworzyć, choć niełatwo tego dowieść. Dla n = 21 można to zrobić w „toporny” sposób, rozpisując wszystkie ogólne schematy N-P (analogiczne jak każdy z trzech powyżej); potem wystarczy zauważyć, że żaden z nich nie składa się z jedenastu N i dziesięciu P.
Jest jednak znany bardziej ogólny i elegancki dowód niemożności utworzenia trójkątów różnicowych rzędu 2^k – 2 (k > 1). Polega on na wykazaniu, że suma liczb w takim trójkącie powinna być parzysta, co prowadzi do sprzeczności, bo dla rzędów określonych podanym wzorem wartości n są nieparzyste (3, 21, 105, 465, 1953, 8001…), a więc suma liczb od 1 do n także musi być nieparzysta. Istnieje wreszcie bardzo pomysłowy, ale trudny dowód, że trójkąty różnicowe rzędu nie mniejszego niż 9 w ogóle nie mogą istnieć. Dla rzędów 6, 7 i 8 ten dowód się nie sprawdza, ale trzy krnąbrne przypadki nietrudno wykluczyć, pisząc odpowiedni program na komputer (nie wspominając o podanych wyżej sposobach dla szóstego rzędu).
Jeżeli z liczb od 1 do 21 usunąć jakąś nieparzystą (ale nie dowolną), zastępując ją kolejną liczbą, czyli 22, to wówczas utworzenie trójkąta różnicowego będzie możliwe, jednak to łamigłówka iście benedyktyńska, niemal wyłącznie guess-and-check. Zdziwiłem się, znajdując takie zadanie (z usuniętą piętnastką) w szkolnym konkursie. Jeśli ktoś zna metodę rozgryzienia tego orzecha na logikę, wdzięczny będę za informację.
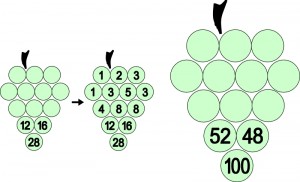
Łamigłówki bliskie trójkątom różnicowym, ale zwłaszcza trójkątowi Pascala, były przed laty w modzie. Pojawiły się między innymi jako Winogrona na Łamigłówkowych Mistrzostwach Świata w Brnie w 2001 roku. Zapraszam do posmakowania lekkostrawnych „owoców” z Mistrzostw, lecz w formie indugadki, czyli reguły zabawy należy samemu wyindukować na podstawie przykładu z rozwiązaniem.
Nietrudno zauważyć, co wspólnego mają Winogrona z trójkątem różnicowym. Wystarczy obrócić kiść z przykładowym rozwiązaniem o 60 stopni zgodnie z ruchem wskazówek zegara.


Komentarze
albo coś ominąłem (bardzo prawdopodobne), albo są 3 rozwiązania:
3 14 1
3 17 15 1
20 32 16
52 48
100
6 10 4
6 16 14 4
22 30 18
52 48
100
9 6 7
9 15 13 7
24 28 20
52 48
100
Warunki zadania są tak ustalone, że rozwiązanie jest jedno.
mp
Niestety będzie to mój ostatni wpis przed urlopem, na szczęście czy też nieszczęście przerwa potrwa tylko/aż tydzień 🙂
A oto rozwiązanie, po obliczeniach matematycznych, już druga próba ‚strzału’ dała porządany rezultat:
__9,_6,_7
_9,15,13,_7
_24,28,20
__52,48
___100
a z wyliczeń wyszło mi tak, że jeśli 3 liczby z górnego rzędu oznaczymy jako a,b i c (tutaj wyszło:a=9, b=6, c=7) to spełniają one dwie równości:
a=2+c
oraz
46=4c+3b
no i tutaj juz zaczalem strzelac:) jak pisalem za drugim razem ustrzelilem:)
Panie Marku, napisał Pan:
„…Ci z Państwa, którzy nadsyłają rozwiązania zadań, stanowią grupę nieoficjalnych przedstawicieli licznego grona …”, a czy mógłby Pan pochwalić się ilu tych czytających jest i jak liczne jest to grono?
Pozdrawiam.
Przepraszam miły Wiązie,
lecz takie statystyki
są w niezbyt dobrym guście
na stronach „Polityki”.
Niechaj więc pozostanie enigmatyczne
„liczne”.
Pozdrav
mp
Fajne zadanko. Myślę, że odpowiedź: 9,6,7 wystarczy. Pozdrawiam.
Witam
Podstawowa reguła uzupełnienia winogron liczbami wydaje się prosta:
liczba w każdym owocu (z wyjątkiem pierwszego rzędu) jest sumą z liczb z owoców z wyższego rzędu stykających się z danym owocem.
Jednak korzystając tylko z tej reguły w zbiorze liczb naturalnych istnieją 4 różne rozwiązania:
_3_14__1
3_17_15_1
_20_32_16
__52_48
___100
_6_10__4
6_16_14_4
_22_30_18
__52_48
___100
__9__6__7
_9_15_13_7
_24_28_20
___52_48
____100
__12__2_10
12_14_12_10
__26_26_22
____52_48
_____100
Niestety przykład ma tylko jedno rozwiązanie w liczbach naturalnych. Brakuje więc mozliwości do porównania i określenia dodatkowego warunku. Dopiero wpis Michała i Pański do niego dopisek o jednym rozwiązaniu zmusiły do poszukania jakiegoś wyróżnika w tych 4 rozwiązaniach.
Jeśli dodakowo przyjmiemy że różnych liczb w rozwiązaniu ma być jak najmniej lub mniej niż 10 to wtedy poprawnym rozwiązaniem jest ostanie (12,2,10)
Wydaje mi się że o to chodzi.
Pozdrawiam
peha
3,14,1
3,17,15,1
20,32,16
52,48
100
No bo pierwsza liczba od góry w rozwiązaniu musi być przez 3 podzielna, z układu równań. Chyba?…
Ja znalazlem 4 rozwiazania i bede sie upieral, ze tyle ich bedzie… (o ile mamy taka sama definicje „induzagadki”: nie dodawaj zasad bez przyczyny)
Najpierw rozwiazania (tylko gorne rzedy)
3 14 1
6 10 4
9 6 7
12 2 10.
Zasada: liczba w kazdym „gronie” jest sumą liczb w gronach powyzej (stykajacych sie).
„Niestety” taka zasada pozwala jednoznacznie rozwiazac przykladowe zadanie i NIE daje sprzecznosci w zadaniu do rozwiazania.
I dlatego uwazam, ze sa 4 rozwiazania, bo teraz jedyne co mi pozostaje to wymyslic dodatkowa zasade przy ktorej bedzie tylko jedno, moga to byc np. (dla opowiednich rozwiazan)
1) Suma wszystkich liczba byla najmniejsza mozliwa; by w drugim rzedzie byla liczba wieksza od innej w rzedzie trzecim
2) (nie mam sensownego pomyslu…)
3) Wiedząc, że różnica liczb w pierwszym rządku wynosi najwyżej 3 (ew. jest najmniejsza mozliwa)
4) np. W drugim i trzecim rządku liczba pojawia się 2 razy; np. umieść liczby tak, żeby była minimalna ilość różnych liczb.
Zdaję sobie sprawę z tego, że propozycje niektorych zasad sa zagmatwane; ale niektore (moze podobne) pamietam z innych zadan. (chyba nie z Łamibloga)
__09__06__07__
09__15__13__07
__24__28__20__
____52__48____
______100_____
W pierwszym rzędzie są liczby jednocyfrowe. Pierwsza i ostatnia liczba w drugim rzędzie są odpowiednio równe pierwszej i ostatniej liczbie w pierwszym rzędzie. Pozostałe liczby są sumami liczb leżących nad nimi.
Najbardziej logicznym rozwiązaniem zadania różnicowego jest zajrzenie do książki Briana Bolta „Matematyczny piknik” zad. 101 odp. na str. 105.
06,20,22,3,21,13 (to pierwszy wiersz)
Wg tego autora jest to jedyne rozwiązanie.
Dziękuję za informację źródłową. Książka jest w stolicy, a ja na prowincji, więc nie mogę do niej zajrzeć, ale domyślam się, że autor nie podał sposobu rozwiązywania.
mp
Zgodnie z Pana domysłem w książce nie ma podanego sposobu rozwiązania, tylko sam wynik. Za to podane są inne informacje o tym problemie. Dokładnie opisany jest on w książce M.Gardnera From Penrose Tiles to Trapdoor Ciphers oraz w artykule C.W. Trigga „Absolute Difference Triangles” w The Journal of Recreational Mathematics z 9(4) 1976-77.
Samodzielnie wymyśliłem to zadanie i rozwiązałem go (program komputerowy) w latach 90-tych. Byłem z siebie bardzo dumny. Potem kupiłem książkę B.Bolta i okazało się, że problem był postawiony i rozwiązany dużo wcześniej. Żeby mieć choć trochę udziału w budowaniu magicznych trójkątów, dodałem warunek, że niektóre liczby są sumą a nie różnicą liczb leżących na nimi .Można zbudować
takie trójkąty z kolejnych liczb od 1 do 15. Np
6 15 1 3 13
9 14 2 10
5 12 8
7 4
11 – suma
Jak było udowodnione nie można zbudować trójkąta z kolejnych liczb od 1 do 21 ale można zbudować taki trójkąt z liczb od 1 do 20 (z obciętym wierzchołkiem) i jest taki trójkąt tylko jeden. Jak on wygląda to zagadka dla czytelników Łamiblogu. Idę spać.
Panie Marku
Ponieważ napisał Pan że „Warunki zadania są tak ustalone, że rozwiązanie jest jedno.”
poproszę o jakiś komentarz gwoli wyjaśnienia.
peha