Z nieskończonością
Jak każdy czytelnik jest pisarzem – najczęściej potencjalnym, tak każdy rozwiązujący zagadki może próbować je układać. Wymyślić oryginalną, ciekawą łamigłówkę nie jest wcale łatwiej, jeśli nie trudniej, niż napisać dobry tekst. Japonia jest jedynym krajem, w którym ranga umysłowego rozrywania się jest na tyle duża, że istnieją tam szkółki (szumnie zwane akademiami) dla przyszłych puzzlemakerów, a w pismach specjalistycznych są obszerne działy, w których młodzi zdolni prezentują nowe pomysły. Od tych działów zaczynam lekturę i zabawę i zwykle na nich kończę; nie ciągnie mnie do standardowych, stadnych typów zadań, które znam na wylot. Co nie mniej ważne, nowe pomysły są dla mnie indugadkami, czyli na podstawie przykładu muszę odgadywać reguły, bo z japońskim u mnie kiepsko. Po wielokrotnym korzystaniu z indukcji można dojść nawet do wniosku, że typowe łamigłówki, w których wiadomo o co chodzi, to tylko półłamigłówki. Prawdziwą sztuką jest rozwiązać zadanie, gdy nie wiadomo, na czym polega rozwiązywanie. Kłania się Piękny umysł. W ciągu kilkunastu lat parę razy się poddałem i prosiłem japońskich kolegów po fachu o podanie zasad. Poniżej jedna z moich klęsk.
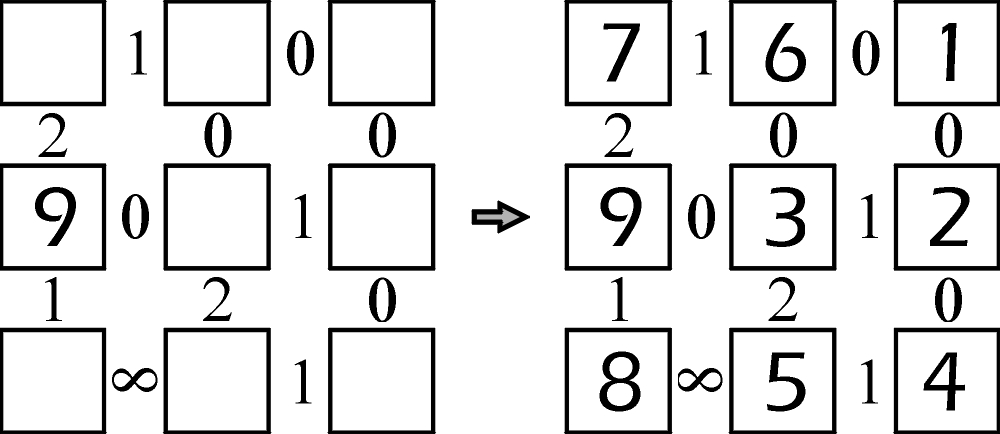
Przykład, czyli małe zadanie plus rozwiązanie, wygląda tak:
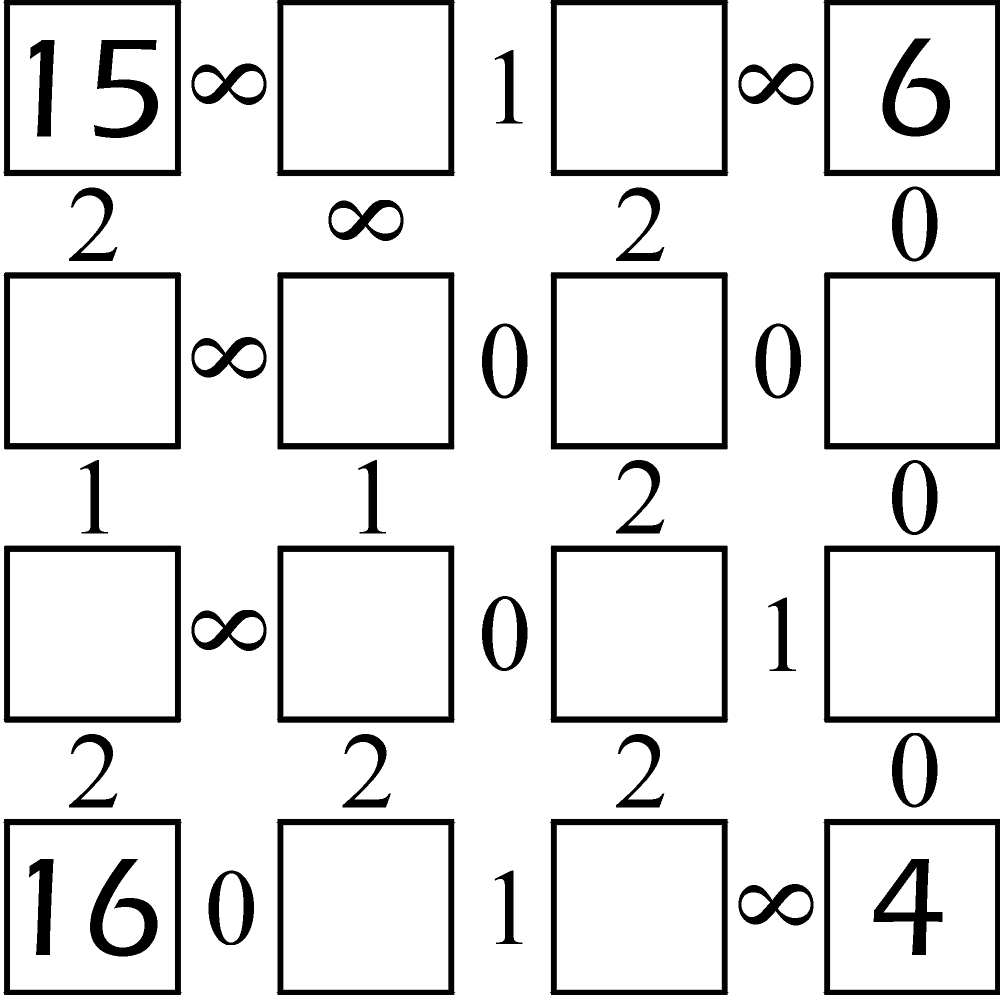
Na jego podstawie należy odgadnąć reguły i rozwiązać zadanie:
Kto pierwszy znajdzie rozwiązanie, otrzyma upominek-nagrodę, do wyboru: jedną z gier – Set!, 6. bierze lub Hive albo książkę Łamigłówki. Podróże w krainę matematyki rekreacyjnej. Wszystkie nadsyłane w komentarzach propozycje reguł i rozwiązań będę ujawniał, ale nie będę komentował. Zabawa jest bezterminowa, czyli trwa do skutku.

Komentarze
Rozwiązanie wierszami:
15, 12, 11, 6
13, 9, 3, 1
14, 10, 5, 2
16, 8, 7, 4
reguła to wpisana pomiedzy kwadraty reszta z dzielenia liczby większej przez mniejszą, jeśli reszta jest większa niż 2 to jest znak nieskonczonosci
15 11 10 6
13 3 12 1
14 10 5 2
16 8 7 4
poprawka:
15 12 11 6
13 9 3 1
14 10 5 2
16 8 7 4
liczby między kratkami mówią ile wynosi reszta z dzielenia większej przez mniejszą (jeśli większe niż 2 to nieskończoność)
Przepraszam za odpowiedź rozciągłą na trzy komentarze, ale zapomniałem dodać, że w diagramie o boku n znajdują się liczby od 1 do n^2
Zasada:
Każda para liczb w kwadratach jest połączona spójnikiem (0,1,2, niesk), będącym resztą z dzielenia większej liczby przez mniejszą (przy czym niesk. oznacza, że R>=3).
Ilość kwadratów wyznacza zakres liczb jakie możemy użyć (3X3 = liczby 1/9; 4×4 = liczby 1/16). Każdej liczby możemy użyć tylko raz.
Rozwiązanie:
15;12;11;6
13;9;3;1
14;10;5;2
16;8;7;4
Rozwiązanie czytane wierszami od góry, od lewej do prawej:
15,12,11,6,
13,9,3,1,
14,10,5,2,
16,8,7,4
Nie doceniłem Państwa. Przepraszam.
Zadanie „padło” błyskawicznie, a w związku z tym nie będę uwalniał komentarzy przed kolejnym wpisem, aby nie psuć zabawy.
Następnym razem spróbuję wybrać coś naprawdę trudnego.
m
Witam
Szkoda że nie jestem pierwszy 😉 Ale co zrobić. Obowiązki.
Moim zdaniem reguły są nastepujące:
Wypełnić pola liczbami od 1 do n gdzie n jest równe ilości pól;
Liczby pomiędzy polami pokazują resztę z dzielenia liczb w danej parze pól. Gdy ta reszta jest większa niż 2 to mamy znak nieskończoności (niewielka ta nieskończoność w tym przypadku)
Rozwiązanie:
15_12_11__6
13__9__3__1
14_10__5__2
16__8__7__4
Pozdrawiam
peha
15 12 11 6
13 9 3 1
14 10 5 2
16 8 7 4
pewnie dobrze reguł nie rozgryzłem, bo wychodzą mi co najmniej dwa rozwiązania
15 12 11 6
13/17 9 3 12
14/18 10 5 4
16 8 7 4
pzdr
15,12,11,6,13,9,3,1,14,10,5,2,16,8,7,4.
15 2 3 6
13 11 5 1
14 12 7 8
16 10 9 4
Na pierwszy rzut oka rozgryzienie reguł wydaje się proste:
-wpisać liczby 1-n, gdzie n to liczba kwadratów
-jeśli między dwoma kwadratami jest 1 lub 2, to tyle wynosi różnica między nimi
-jeśli tam jest 0, to jedna z liczb jest dzielnikiem drugiej
-jeśli jest tam symbol nieskończoności, to różnica jest większa od 2
-znaki między kwadratami można stosować wymiennie
Zakładając takie reguły, małe zadanie ma jednoznaczne rozwiązanie, ale duże nie wychodzi (nie zgadza się tylko z jednym polu, nad czwórką).
Rzeczywiście twardy orzech.
15 12 11 06
13 09 03 01
14 10 05 02
16 08 07 04
Zasady: Wpisz do diagramu liczby od 1 do n^2 (n – długość boku kwadratu). Podane liczby między polami oznaczają resztę z dzielenia większej liczby przez mniejszą. Jeśli reszta jest większa od 2 to podano nieskończoność. Niektóre liczby zostały już wpisane.
15 12 11 6
13 9 3 1
14 10 5 2
16 8 7 4