Antymagia
Kwadrat 3 x 3 można wypełnić liczbami od 1 do 9 na 9!/8 = 45360 różnych sposobów (z dokładnością do obrotów i odbić lustrzanych). Tylko jedno z tych wypełnień ma niezwykłą własność: sumy liczb w wierszach, kolumnach i na przekątnych są takie same. Ten unikatowy egzemplarz, jako układ liczb zwany w matematyce matrycą kwadratową drugiego stopnia, kojarzony w starożytności i w średniowieczu z siłami nadprzyrodzonymi i mistyką, pojawiał się na talizmanach i amuletach jako kwadrat magiczny – i takim pozostał.
Arabski talizman jest nieco zagadkowy. Znadujące się na nim liczby i sumę magiczną łatwo rozszyfrować, ale dlaczego suma jest właśnie taka?
Na temat kwadratu magicznego 3 x 3 i jego nieco młodszych, większych kuzynów wylano od średniowiecza morze atramentu. Zagadnienie jest w zasadzie rozrywkowe, ale nie brakuje prac stricte matematycznych. Na fali mody na sudoku temat powrócił i pojawiły się kolejne dziełka, że tak powiem, podsumowujące całokształt; najnowsze jest tu.
Przed półwieczem kwadratomaniacy wymyślili antymagię – sumy liczb w wierszach, kolumnach i na przekątnych powinny być różne. Takich kwadratów 3 x 3 jest 3120, więc nie stanowią niczego niezwykłego. Dlatego z czasem pojęcie antymagii ograniczono do kwadratów, w których wszystkie sumy tworzą fragment ciągu liczb naturalnych. Okazało się jednak, że antymagicznych kwadratów 3 x 3 nie ma – ciąg sum zawsze będzie przerwany. Można jednak uznać za prawie antymagiczny kwadrat 3 x 3, w którym pojawia się ciąg liczb od 1 do 16 oraz tajemnicza liczba x > 17. Liczby od 1 do 9 wpisane są w diagram, a liczby od 10 do 16 oraz x są sumami.
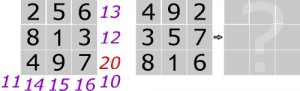
Z lewej strony przykład (x = 20), z prawej zadanie domowe: w kwadracie magicznym należy przestawić cztery liczby tak, aby powstał prawie antymagiczny.
Piszemy o tym, co ważne i ciekawe
Mocne canadiano
Nowy premier Kanady Mark Carney jest chodzącym wzorcem wszystkiego, czego Donald Trump nienawidzi najbardziej. Czy będzie też prorokiem antypopulistycznej reakcji?
Dla ułatwienia, bo zadanie jest trudne: x > 20, trzy z czterech przestawianych liczb są w tym samym rzędzie, a rozwiązania są przynajmniej dwa (przynajmniej tyle znam).
A gdyby ktoś miał ochotę przejść do historii matematyki, może spróbować znaleźć prosty dowód niemożności utworzenia kwadratu antymagicznego 3 x 3. To nie żart, nikomu dotąd się to nie udało. Chodzi oczywiście o logiczny dowód, a nie sprawdzenie przy pomocy komputera, że żaden z 3120 heterokwadratów 3 x 3 (tak obecnie określa się te, w których wszystkie sumy są różne) nie jest antymagiczny.



Komentarze
Są cztery rozwiązania:
—–4–9–1–14
—–3–5–7–15
—–6–8–2–16
12-13-22-10-11
—–4–9–2–15
—–3–6–7–16
—–5–8–1–14
13-12-23-10-11
—–8–2–4-14
—–3–5–7-15
—–9–1–6-16
18-20-8-17-19
—–9–2–5-16
—–3–4–7-14
—–8–1–6-15
17-20-7-18-19
Może to nie jest najistotniejsze w artykule, jednak drugie zdanie wydaje się nie być co końca prawdziwe (czy może lepiej zabrzmi „logiczne”).
Skoro w pierwszym zdaniu ilość rozwiązań podana jest „(z dokładnością do obrotów i odbić lustrzanych).” to w takim wypadku, w określonym zbiorze, magicznych kwadratów jest osiem a nie jeden.
Co nie zmienia faktu że artykuł jest bardzo ciekawy, pozdrawiam.
Przestawiane sa cyfry w dolnym rzedzie (wierszu), a rozwiazania sa rzeczywiscie tylko dwa (dla x > 20):
491
357
682 x=22
492
367
581 x=23
a
Dziękuję.
Magiczne jest jedno z 45360 ustawień.
Określenie „z dokładnością do obrotów i odbić lustrzanych” oznacza, że jeśli jakieś ustawienie można utworzyć, obracając lub/i odbijając inne, to oba te ustawienia uważa się za jednakowe.
Czyli summa summarum moim zdaniem wszystko gra.
Pozdrav
m
Witam dostałem zagadkę od znajomych, która chyba ma coś wspólnego kwadratem antymagicznym. Szukałem kombinacji, która by dała taki wynik, ale jakoś nie mogę znaleźć, a najgorsze, że nie wiadomo czy trzeba uzupełnić liczbami od 1 do 9 czy też większymi.
link do zadania:
http://img22.imageshack.us/img22/3179/kwadratantymagiczny.jpg
Będę wdzięczny za pomoc
Pozdrawiam
Sonus
Nie można wypełnić tego kwadratu zgodnie z podanymi warunkami. W tym kwadracie i w każdym innym suma wierszy musi być równa sumie kolumn, bo liczby w wierszach i kolumnach są te same.
HM, moim zdaniem zadanie NIE ma rozwiazania.
Sume wszystkich liczb w kwadracie magicznych mozna dostac albo poprzez zsumowanie sum wierszy (wychodzi 54) lub poprzez zsumowanie sum kolumn (wychodzi 45). Takze albo cos jest nie tak z obrazkiem, albo ktos Cie robi w konia;)
pozdr
Jeśli to jest kwadrat antymagiczny, który jest mi znany, to błąd polega na tym, że zamiast 19 powinno być 10.
m