Kwadratowo
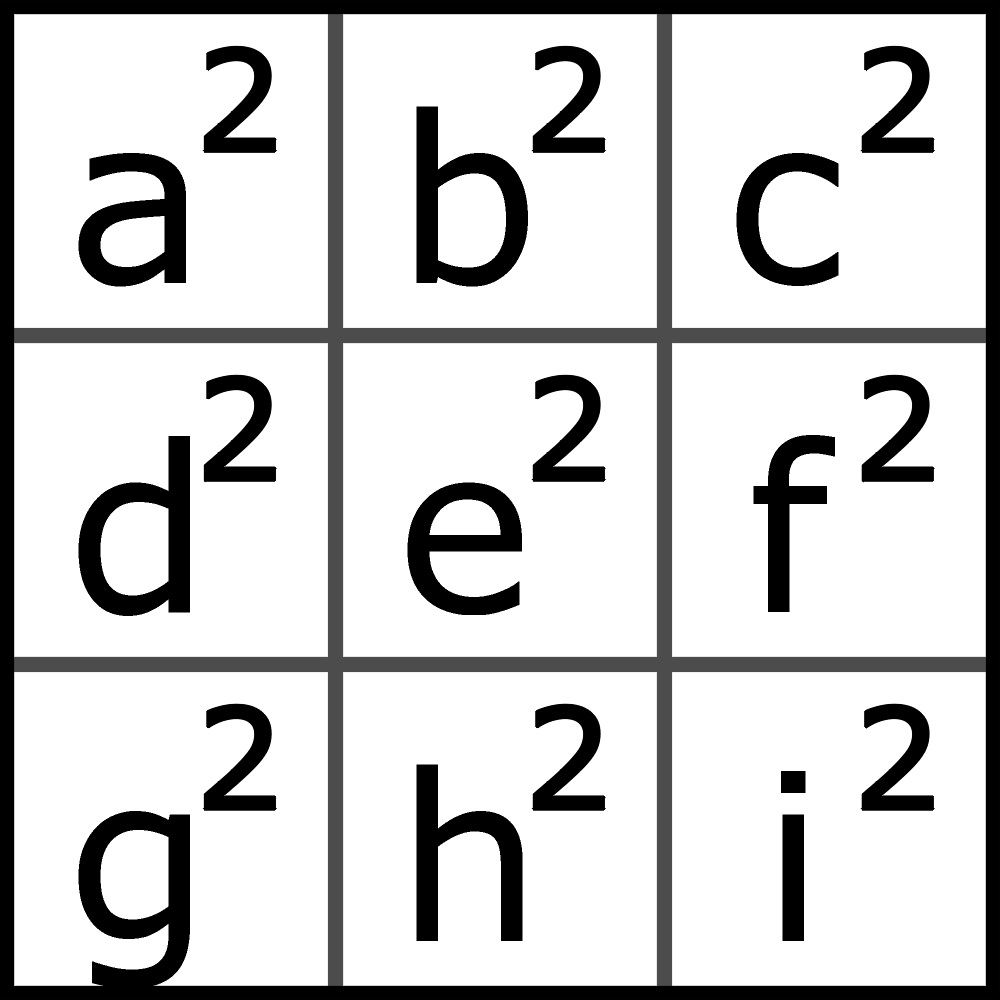
Wspominałem już w paru miejscach (w minionym roku w Łamiblogu, a ostatnio w artykule „Miliony za myślenie” w numerze specjalnym Wiedzy i Życia) o nagrodzie, czekającej na tego, kto ułoży kwadrat magiczny 3×3 złożony z kwadratów, czyli coś takiego:
Dla porządku przypominam, że sumy trójek liczb (w tym przypadku kwadratów liczb) w każdym rzędzie, czyli w każdym wierszu, kolumnie i na obu przekątnych, powinny być takie same.
Nagroda jest więcej niż skromna – 100 $ + 100 euro + butelka szampana – ale lepszy rydz… Poza tym pieniążki czekają na kontach i procentują od lat trzynastu (dolary) i pięciu (euro), więc pula pewnie już się podwoiła. Szampan też chyba (?) im starszy, tym lepszy.
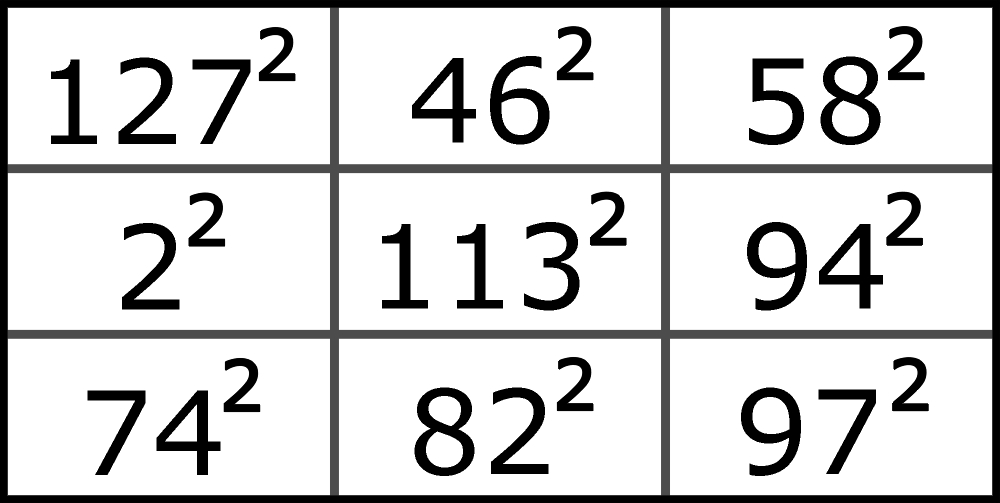
Dolarami sypnął sam Martin Gardner, euro i szampanem (chlusnął) – matematyk francuski Christian Boyer za na pozór prostsze zadanie: wystarczy, że kwadratami będzie tylko siedem z dziewięciu liczb. Jeden kwadrat w wersji Boyera znaleziony przed ufundowaniem nagrody, wygląda tak:
Euro i szampan otrzyma znalazca drugiego, ale całkiem innego kwadratu, czyli takiego, który nie będzie jakimś przekształceniem powyższego. Warto dodać, że na nagrody zasłuży także ten, kto udowodni, że jedno lub drugie zadanie jest niewykonalne.
Kilka dni temu Robim64 napisał w komentarzu pod poprzednim wpisem na ten temat, że znalazł drugi kwadrat. Oniemiałem z wrażenia, bo prędzej spodziewałbym się 100-procentowej frekwencji w eurowyborach. Okazało się, niestety, że nowy kwadrat jest dość prostym przekształceniem starego: podstawa każdej drugiej potęgi jest podwojona, a dwie liczby, które nie są kwadratami, pomnożone są przez cztery, czyli suma magiczna jest czterokrotnie większa (2 167 500).
Istnieje też drugie uproszczenie zadania Gardnera, które można by nazwać wersją Sallowsa (Lee Sallows – informatyk holenderski z uniwersytetu w Nijmegen): kwadratami powinny być wszystkie liczby, ale w jednym z ośmiu rzędów suma trzech liczb może nie być magiczna. Ta wersja wydaje się bliższa ideału, bo magicznych jest siedem sum z ośmiu, a w wersji Boyera kwadratami jest siedem liczb z dziewięciu. Sallows znalazł jeden taki kwadrat („zakałą” jest suma na przekątnej łączącej lewy górny róg z prawym dolnym – 38307, pozostałe równe są 21609):
Za znalezienie drugiego takiego kwadratu nie ma nagrody, więc szukają tylko wolontariusze. Jak dotąd też bezskutecznie.
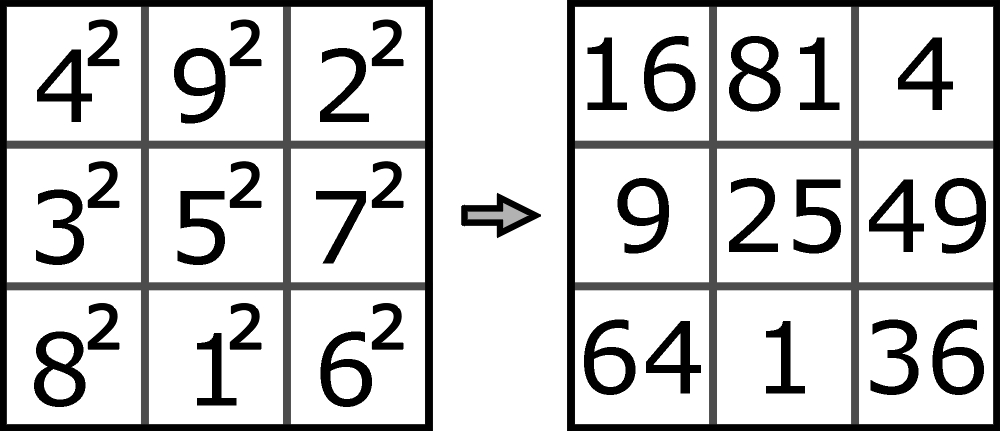
Jako zadanie domowe proponuję spróbować „ukwadratowić” jedyny klasyczny kwadrat magiczny 3×3, znany od paru tysięcy lat:
Jeśli wszystkie liczby podniesiemy do kwadratu, to magia oczywiście zniknie:
Ale nie do końca, czyli nie powstał tzw. kwadrat antymagiczny (osiem różnych sum), bo w dwóch wierszach sumy są takie same (101) i w dwóch kolumnach również, choć inne niż w wierszach (89).
Czy można zwiększyć magiczność tego kwadratu, czyli przestawić liczby tak, aby równe sumy były w więcej niż dwóch rzędach? A jeżeli tak, to w ilu najwięcej? A jeżeli nie, to dlaczego?



Komentarze
Z dziewięciu liczb możemy wybrać trójki liczbowe na 84 sposoby. Wśród sum różnych trójek tylko suma równa 101 powtarza się więcej niż 2 razy. Jest to:
1+36+64=101
4+16+81=101
16+36+49=101
Wśród wymienionych składników dwukrotnie występuje 36 i 64. Zatem te liczby muszą wystąpić na skrzyżowaniu kolumn i wierszy lub przekątnych kwadratu. W wolne miejsca wpisać jeszcze brakujące 9 i 25. Rozwiązań jest wiele; jednym z nich jest:
16_36_49
_4__1__9
81_64_25,
gdzie pierwszy wiersz oraz pierwsza i druga kolumna daje w sumie 101.
Pozdrawiam
Sumy mogą być sobie równe w maksymalnie trzech rzędach. Takich układów liczb od 1 do 9 jest sporo. Jeden przykładowy
| 89
01 04 09 | 14
36 16 49 | 101
64 81 25 | 170
————–|———–
89 101 101| 042
Sumy w trzech rzędach są równe 101.
Jeśli dobrze rozumiem (a rzadko mi się to zdarza 🙂 ) to żeby mieć więcej niż dwa wiersze, pozostaje nam tylko 3 🙂 suma wszystkich liczb to 285.
285/3=95. Musimy znaleźć 3 wiersze z taką sumą w każdym z nich.
Aby to sprawdzić wystarczy wybrać dowolną liczbę m na przykład 81 i wtedy 95-81=14. Nie jesteśmy w stanie uzyskać sumy 14 z dwóch liczb, które mamy do wyboru. Wniosek: nie będziemy mieli 3 wierszy z tą samą sumą. c.n.d.
innym pytaniem jest to czy pod pojęciem wiersza możnaby ująć kolumnę, czyli na przykład mamy dwa wiersze i jedną kolumnę o tej samej sumie….
no, ale będąc w pracy więcej nie mogę w tej chwili pomóc:)
Wystarczy zamienic miejscami dwie liczby w gornym i wierszu i dwie w dolnym, aby w trzech rzedach wystapiła suma 101 (dwa te, co były i prawa kolumna):
4 81 16
9 25 49
1 64 36
Nie da sie zrobic tak, zeby suma byla taka sama w czterech rzedach.
a
🙂 za mało rozwiązuje zadań chyba:):) bo dla mnie rząd równoważny jest z wierszem, dla mnie oba te wyrazy są ‚poziome’ a kolumna to kolumna – pionowa 🙂 mea culpa 🙂
Ciekawe, jeśli mielibyśmy jakąś salę z krzesłami, na przykład kwadrat 10 na 10, równo rozstawione. Ciekawe jak by ludzie zajmowali miejsca, gdyby im powiedzieć żeby zając tylko te w pierwszym rzędzie 🙂
W sumie ciekawe zagadnienie, bo wychodzi na to, że rząd to albo kolumna albo wiersz (w tym zadaniu), ale pytanie czego to dotyczy (okreslenie rzedu jako kolumny lub wiersza)? Bo jeśli wspomnianych krzeseł czy innych rzeczy to już tak nie jest, a jeśli chodzi o macierze (powiedzmy, że wygląd kwadratu 3×3 jest podobny do macierzy) to rząd w macierzy to już zupełnie inna historia. Szukałem, ale jakoś nie mogłem znaleźć określenia rzędu jako kolumny lub wiersza.
No ale te rozważania to tak już na zupełnym marginesie.
A wracając do tej sali z krzesłami, jakby je rozstawić, te krzesła, nie w tą samą stronę , ale przypadkowo, każde ‚siedzeniem’ w losową stronę, ciekawe co byłoby wyznacznikiem takiego ‚rzędu’. Myślę, że w tym przypadku byłoby to biurko albo tablica w tej sali, czy też scena lub cokolwiek co by stanowiło jakiś główny punkt tej sali.
Ale to już jeszcze dalszy margines ‚teorii rzędów’ 😀 .
P.S.
Jeszcze jeden kamyczek do terorii rzędów:)
Znalazłem kilka zadań w których użyto sformułowań typu: „…w każdym rzędzie i w każdej kolumnie…”, i to zadań ze stowarzyszeń zajmujących się łamigłówkami, czyli raczej znających się na układaniu poleceń. Można pogooglować… 🙂
Czy tę flaszkę z dwoma setkami dostanie się też gdy liczby w kwadracie będą nie naturalne, a częściowo całkowite ujemne lub wymierne?
Wiąz:
Z rzędami, wierszami i kolumnami sprawa jest umowna. Ważne, żeby było wszystko jasne.
Dla mnie rząd jest bezkierunkowy, a żeby nie pisać „rząd poziomy” i „rząd pionowy” stosuję terminologię tablicową, czyli „wiersz” i „kolumna”. W przypadku bliźniaczych macierzy też tak jest przyjęte, więc chyba tak jest lepiej.
Rząd krzeseł w kinie to jednak co innego, podobnie jak kolumna w wojsku (tu zamiast wierszy są szeregi).
Org:
Niestety, tylko naturalne.
m