Wielopłaszczyznowo
Komentarze towarzyszące nadsyłanym przez Państwa rozwiązaniom są często ciekawe i inspirujące. Zamieszczone pod poprzednim wpisem także skłaniały do przemyśleń i… wspominków.
Robert_C dopominał się deseru dla smakoszy w postaci zadania trójwymiarowego. Jeżeli miałoby ono być ścisłym odwzorowaniem zadania z podziałem figury i składaniem kwadratu, to należałoby dzielić na dwie części jakąś „niekształtną” bryłę złożoną z n^3 sześcianików tak, aby z tych części można było złożyć sześcian. Obawiam się, niestety, że układanie, a zwłaszcza rozwiązywanie takiego zadania byłoby niezbyt zachęcającym, benedyktyńskim zajęciem, choć nie wykluczam, że ktoś by się na nie skusił. Zakładam oczywiście, że autor zadania nie ograniczyłby się do byle jakiego rozcięcia sześcianu i połączenia otrzymanych dwu kawałków w jakiś przypadkowy sposób.
Ten pomysł przypomniał mi jednak podobną grę-zabawkę o nazwie Superfection, popularną w Anglii w latach 70. i 80. ubiegłego wieku.

32 „postrzępione” klocki należało sczepić parami tak, aby powstało 16 sześcianów, a każdy sześcian umieścić na odpowiednim polu planszy 4×4. Wygrywał, kto szybciej się z tym uporał. Adresowana głównie do starszych dzieci gra uchodzi za bardzo pożyteczną „klasykę” – wyrabia spostrzegawczość, zręczność palców, ale przede wszystkim jest jedną z najlepszych kształtujących wyobraźnię przestrzenną maluchów. Gdyby była dostępna, to bym polecał.
Wracając do Państwa komentarzy, spodobał mi się podany przez tarię zwięzły opis sposobu rozwiązywania, a zwłaszcza zauważenie logicznego fundamentu zadania: jeśli rozetniemy kwadrat na dwie części, to co najmniej dwa z jego boków nie zostaną podzielone. Łamigłówkowym wyjadaczom może się to wydać niezbyt odkrywcze, ale jednak uchodzi uwadze bardzo wielu rozwiązujących.
I wreszcie najważniejsze: dodatkowe rozwiązania podane przez Jazz_ona… Szczególnie drugie zwaliło mnie z nóg oryginalnością. Właściwie mój komentarz jest zbyteczny, wystarcza podziw oraz gratulacje i to podwójne: dostrzeżenia na pozór nieistotnego drobiazgu, czyli braku informacji, że części nie mogą składać się z kawałków połączonych tylko rogami oraz znalezienia rozwiązań wykorzystujących to niedopowiedzenie. Aby wszystko było widoczne jak na dłoni, narysowałem trudniejsze „odkrycie” Jazz_ona – obrazek robi większe wrażenie niż symboliczny zapis.
Raczej nie będę ryzykował zamieszczania trójwymiarowych zadań „manipulacyjnych”. Takie zabawki najlepiej funkcjonują w wersji 3D, czyli po prostu w dłoniach. Natomiast proponuję, nie po raz pierwszy zresztą, coś wielopłaszczyznowego.
Oto cztery L-kształtne figury. Każda złożona z czterech kwadratów – białych i czerwonych.
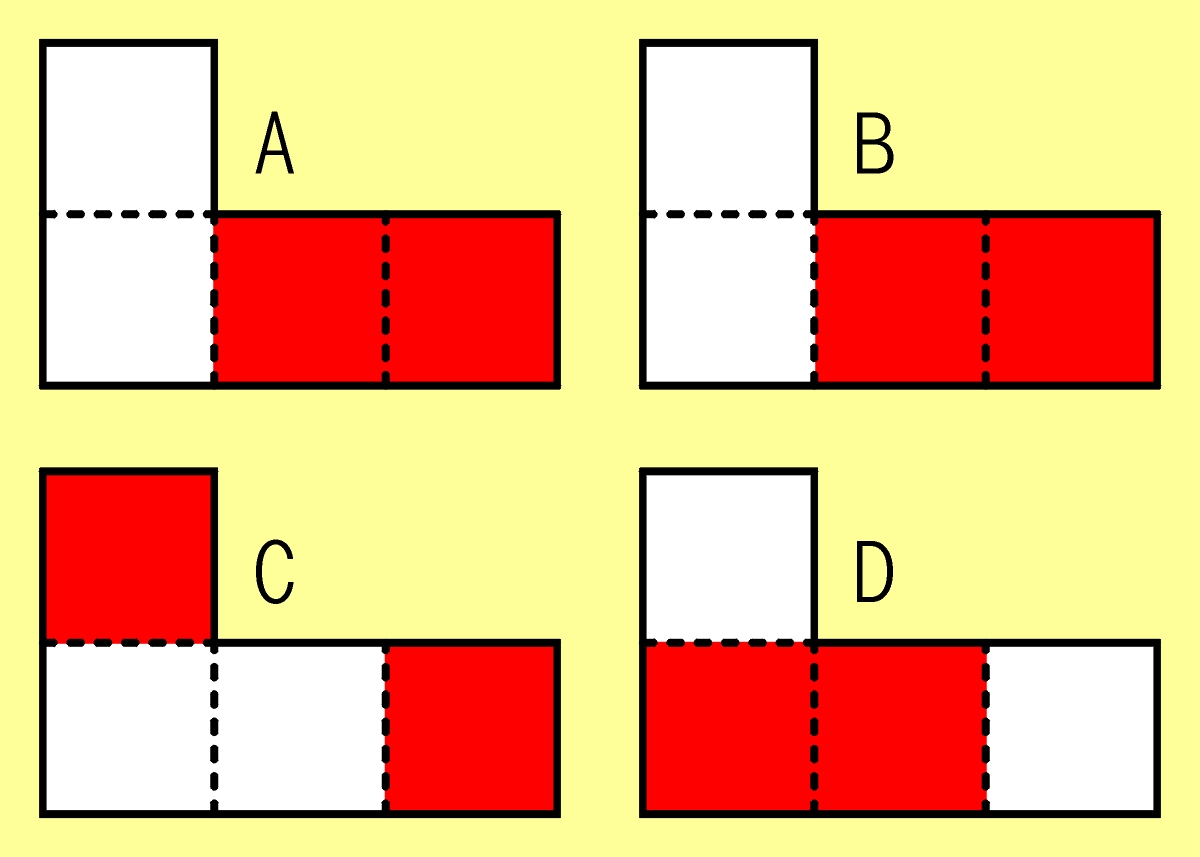
Zadanie polega na tym, by „spleść” je z sobą (nie są całkiem sztywne) tak, aby wszystkie białe kwadraty zostały schowane pod spód, czyli na wierzchu widoczne były wyłącznie czerwone. Figur nie można zginać, a tylko delikatnie wyginać przy splataniu, jeśli będzie konieczne ukrycie białego kwadratu pod czerwonym.
Gwoli jasności przykład z błędem (wystaje jeden biały) oraz sposób zapisu rozwiązania.
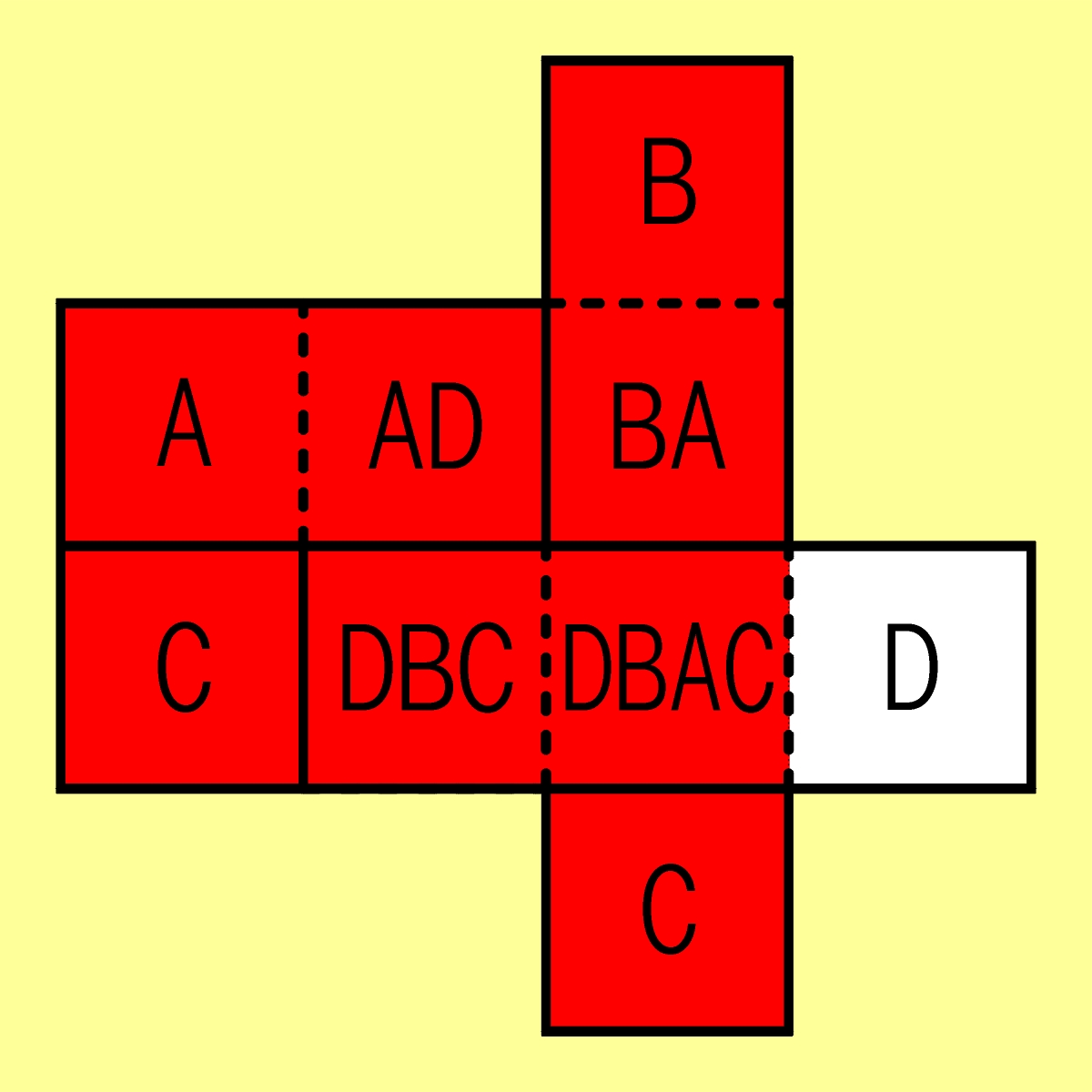
————-B
A—AD—BA
C-DBC-DBAC-D
————–C
Litera w grupie znajdująca się bardziej na prawo oznacza kwadrat danej części umieszczony niżej (polecam wstawianie kreseczek zamiast spacji, bo tekst może się „rozjechać”).
Jeśli komuś z Państwa uda się rozwiązać zadanie wyłącznie w głowie, czyli bez wycinania i pasowania „elek”, może przyznać sobie tytuł Jamesa Bonda wyobraźni wielopłaszczyznowej.
PS Deser dla smakoszy: czy da się spleść figury tak, aby pod spód schowały się wszystkie czerwone?

Komentarze
Przede wszystkim dziękuję za gratulacje. Zawsze to miłe i mobilizujące.
Naszła mnie taka refleksja, że chyba najciekawszymi zadaniami są te, które sformułowane są z takimi niby niedomówieniami, czy też powiedziane jest coś niby nieistotnego. I szczególną ma się satysfakcję, gdy to się zauważy i wykorzysta w rozwiązaniu. Inaczej jednak bywa wtedy, gdy są to „wpadki” jakich niedawno doświadczyli układający zadania testowe do gimnazjum czy na maturę. Kończąc komentarz do poprzedniego wpisu, chciałbym zauważyć, że metoda zastosowana przez tarię może nie być efektywna, gdy dopuścimy niespójność części. Łatwo o przykład. Wyobraźmy sobie, że typową szachownicę dzielimy na dwie części, jedną złożoną z pól białych, drugą zaś – z czarnych. Wówczas podzielone zostają wszystkie cztery boki szachownicy.
Jeszcze raz dziękuję za miły komentarz.
Z pozdrowieniami,
Jazz_off
Udało mi się rozwiązać zadanie w pamięci, bez dodatkowych rekwizytów, choć myślałem, że polegnę.
Oto rozwiązanie:
.DA….CD
DAB..ABC..A
.CD….BC
………..B
Przypuszczam, że mogą być jeszcze inne rozwiązania, nie licząc – oczywiście – obrotów.
Z pozdrowieniami,
Jazz_off
Ja rozwiązałam niestety z wycinaniem.
Czerwone na wierzchu:
___ AB ___ ___
CD.ABC.BC.-B
DA–DA-CD.
Białe na wierzchu:
ADB-DCB–B
AD—CA—BA
DC—-C
Walki o szlachetny tytuł Jamesa Bonda wyobraźni wielopłaszczyznowej nie podjąłem i poszedłem drogą wycinania i pasowania „elek”, bo tak było łatwiej.
1. Czerwone na wierzchu (jedno z rozwiązań):
—CD–DB—DB
A–AC–BAC-CD
———BA—–
2. Czerwone pod spodem (jedno z rozwiązań):
B——BA—-
DCB–CA–C
ADB–AD–DC
Pozdrawiam
Gdy Pan Marek umieszcza wpis tak wcześnie, to oczywiście musi być błąd – no i jest. Rozwiązanie mam dobre tylko było błędnie zapisane. A oto poprawny zapis:
DA – CD
DA – ABC – AB
CD – BC
– – B
A teraz czas na deser:
ADB – DCB – B
AD – CA – BA
DC – C
Z deserem poszło mi dużo szybciej pomimo, że nie mam żadnej sensownej metody – trochę szczęścia, trochę wyobraźni.
Pozdrawiam,
Jazz_off
nie wycinałem elek, ale narysowałem sobie najpierw klocki, a potem końcowe rozwiązanie na kartce, więc w głowie go nie zrobiłem
DA-CD
DA-ABC-AB
CD-BC
__-B
aha, da się też oczywiście zostawić białe na górze. podejrzewam, że rozwiązań może być sporo, bo coś za szybko na jedno wpadłem
ADB-DCB-B
AD-CA-BA
DC-C
Zadanie chyba nie należy do najtrudniejszych. Tylko z pomocą ołówka szybko odnalazłem:
____AB
CD_ABC__BC___B
DA__DA__CD
Deser także szybko zniknął (to znaczy zniknęły wszystkie czerwone kwadraty) w następującym układzie:
DC__AD__ADB
_C__CA__DCB
____BA____B
Podobnie jak Tomkowi, stosunkowo szybkie znalezienie rozwiązania pozwoliło mi przypuszczać, że istnieją inne rozwiązania. Obroty i zamiana figury A z B – z oczywistych powodów – uważam za jedno rozwiązanie. Nie chciało mi się ich szukać licząc na to, że ktoś je poda.
Ku mojemu wielkiemu zdziwieniu wszyscy podali to samo rozwiązanie zadania głównego i deseru. Czy jest to przypadek, czy też nie istnieją inne rozwiązania? Andrzeju, napisałeś w swoim komentarzu, że podajesz jedno z rozwiązań. Czy masz inne?
Z pozdrowieniami,
Jazz_off
W komentarzach, rozwiązanie zadania głównego zostało podane na dwa sposoby.
Jeśli chodzi o „deser” (czerwone pod spodem), to rzeczywiście,zastanawiające jest, że wszyscy podali to samo rozwiązanie.
Pozostałe „desery”:
1.
B—–BA——
DBC–CA–C
ADB–AD–DC
2.
A—–AB—
DCA–CB–C
BDA–BD–DC
3.
A—–AB——
DAC–CB–C
BDA–BD–DC
Być może, że istnieją jeszcze inne rozwiązania.
Pozdrawiam