Sofimetria
Od bardzo dawna ludzkość tkwi w wielu tzw. mylnych błędach przekazywanych z pokolenia na pokolenie. Co gorsza niektóre z nich dotyczą podstaw nauk ścisłych i wpajane są dzieciom w szkołach. Jednym z tych, które należałoby czym prędzej poprawić, jest wzór na powierzchnię kuli. Nawet nie będę przypominał tej żałosnej gafy powielanej w podręcznikach do geometrii. Podam od razu, jak być powinno:
S = pi^2*R^2,
a nawet udowodnię.
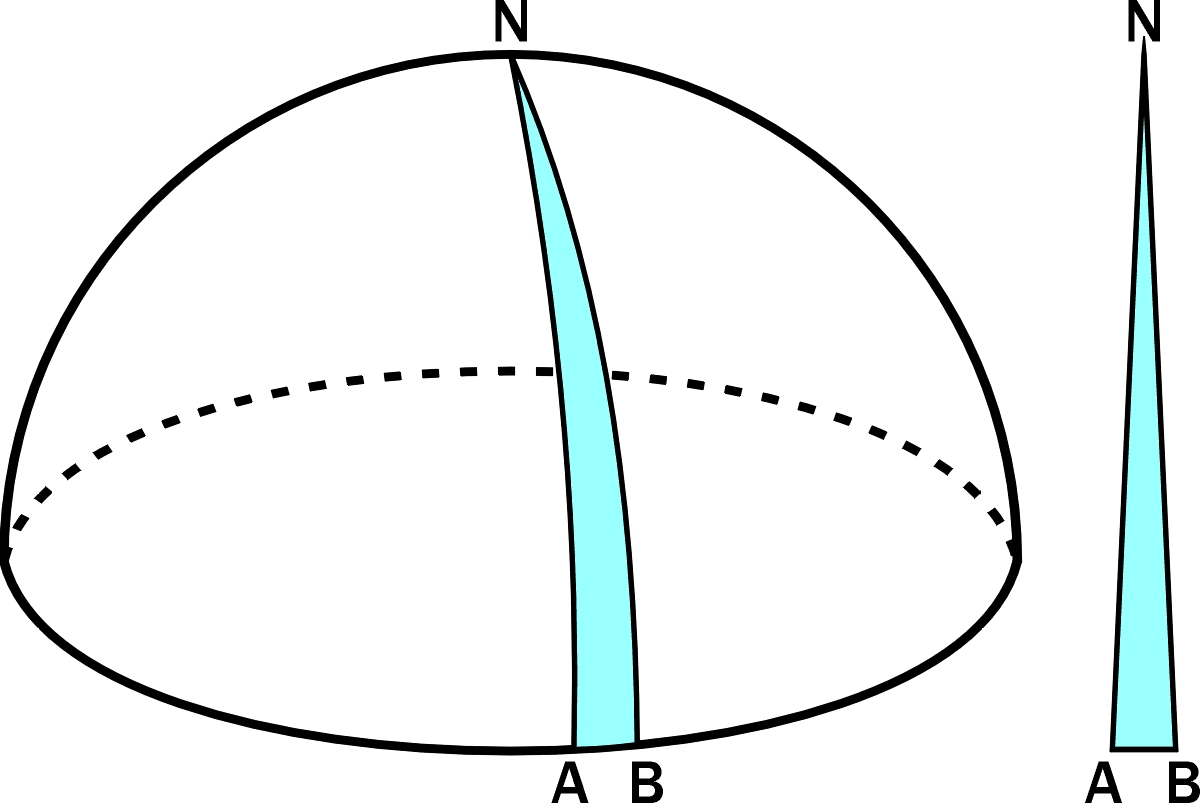
Weźmy półkulę o promieniu R, zaznaczmy biegun (N) i podzielmy równik na n bardzo małych, ale równych części. Z kolei oznaczmy na półkuli wąski mini-trójkąt o podstawie AB umieszczonej na równiku i równej długości jednej z tych n części oraz o wierzchołku na biegunie N. Podstawa tego trójkąta będzie oczywiście równa 2pi*R/n, wysokość pi*R/2 (ćwiartka obwodu), czyli pole powierzchni wyniesie pi^2*R^2/2n. Powierzchnia półkuli będzie równa sumie powierzchni tych wąskich trójkącików, czyli pi^2*R^2/2, zaś powierzchnia kuli będzie dwa razy większa, a więc wyniesie pi^2*R^2.
Mam nadzieję, że Wysoka Komisja doprowadzi wreszcie do zmian w encyklopediach i podręcznikach, a ja tymczasem zajmę się owcami.
Najładniejszy z poprawnych dowodów to ten, który jest krótko, zwięźle i jasno sformułowany oraz ewentualnie sprytny. W związku z tym spośród nadesłanych rozwiązań zadania o rozkułaczaniu górali-owczarzy do nagrody zostali nominowani autorzy dowodów najbliższych następującemu, który udało mi się zmieścić w jednym zdaniu złożonym:
Skoro liczba wszystkich owiec równa jest 128, czyli jest siedmiokrotnie 
parzysta, to po pierwszym rozkułaczeniu każdy góral będzie miał liczbę owiec podzielną przez dwa, po drugim – podzielną przez 4, po trzecim – przez 8, a po n-tym – przez 2^n; zatem po siódmym (2^7 = 128) wszystkie owce trafią do jednego górala.
Operowanie konkretnym przykładem, zwykle sprowadzającym się do sytuacji początkowej {1, 1, 2, 4, 8, 16, 32, 64}, trudno uznać za dowód. To raczej rozwiązanie innego zadania, polegającego na ustaleniu, ilu było co najwyżej górali z owcami, jeśli nastąpiło siedem „transferów”.
Zwycięzcą (wylosowanym) został maczek. Laureata proszę o kontakt pod adresem m.penszko@polityka.com.pl w celu ustalenia sposobu przekazania nagrody. Jest nią owczywiście gra „Owczy pęd” ufundowana przez wydawnictwo Egmont.
Zapraszam do następnych konkursów. Kolejny niebawem.
Komentarze
Jak tylko Wysoka Komisja doprowadzi do wspomnianych zmian za namową Pana Marka, proponuję czym prędzej zwrócić się do wszystkich Biur Kartograficznych, aby w związku z zaistniałymi zmianami uznały w końcu, że kula jest jak najbardziej rozwijalna, czyli odwzorowywalna na płaszczyźnie w taki sposób, aby wszystkie łuki zachowały swoją długość. Dzięki spostrzeżonej gafie bedziemy mogli cieszyć się nowymi, dokładnymi papierowymi mapami.
Komentarze, oprócz pełnych entuzjazmu i podziwu dla mojej propozycji poprawienia wzoru, uwolnię w najbliższy piątek (entuzjastyczne uwalniam natychmiast).
mp
Oszustwo polega na tym, że trójkąta ABN nie da sie „rozprostować” do postaci płaskiego trójkąta, pokazanego na prawym rysunku (sfera nie jest powierzchnia prostokreślną). Skoro mozna powierzchnię kuli podzielić promieniście na plasterki, to mozna jeden z takich trójkątnych plasterków pociąć poziomo na kawałki „trapezowe”. W płaskim trójkącie średnia arytmetyczna podstaw takiego trapezu byłaby wprost proporcjonalna do odległości tego plasterka od wierzchołka trójkąta. A jak jest w trójkącie narysowanym na sferze? Otóż średnia długości podstaw trapezu byłaby oczywiście równa obwodowi koła, podzielonemu na n części, tak jak to zostało zrobione z równikiem. A jaka jest długość obwodu takiego koła? Łatwo zauważyć, że jeżeli opiszemy położenie trapezu kątem między promieniem przechodzącym przez jego środek a płaszczyzna równika, to promień okręgu, zawierającego poziomą linię, przechodzącą przez środek trapezu, jest równy promieniowi kuli pomnożonemu przez sinus tego kata. Czyli zamiast zależności liniowej mamy zależność sinusoidalną i np. w jednej trzeciej wysokości (liczonej od wierzchołka) trójkąt ma szerokość 1/2 a nie 1/3, a w połowie wysokości 0,707 a nie 0,5. Czyli po rozprostowaniu trójkąt „napęcznieje” po bokach. I właśnie w tym napęcznieniu tkwi różnica między prawidłowym wzorem na powierzchnię kuli, a wzorem sofizmatycznym
Podziwiam umiejetnosc rysowania „trojkata” o dwoch katach prostych 🙂
Błąd w rozumowaniu Gospodarza polega oczywiście na tym, że wycinek półsfery narysowany przez niego nie jest płaskim trójkątem. Wycinka tego nie da się spłaszczyć, czyli przenieść na płaszczyznę tak, żeby zachować długości wszystkich linii i wartości kątów, jednak na pierwszy rzut oka widać, że ‚w połowie odległości’ od wierzchołka N jest on szerszy niż trójkąt równoramienny o podstawie 2piR/n
Z trójkątów równoramiennych narysowanych obok można złożyć powierzchnię boczną ostrosłupa prawidłowego o podstawie n-kąta foremnego, która, jako żywo, pólkuli nie przypomina. Przy dużej wartości n przypomina jednak powierzchnię boczną stożka o tworzącej długości pi*R/2 i promieniu podstawy R, której miarę udało się Gospodarzowi uzyskać 🙂
Przede wszystkim gratuluję Maczkowi, podobał mi się jego sposób dowodzenia. Jest, zwięzły i bez niedomówień.
Natomiast nie pojąłem jak Pan, Panie Marku, z założenia, że „liczba wszystkich owiec równa jest 128” wywiódł, że po pierwszym rozkułaczeniu każdy góral będzie miał liczbę owiec podzielną przez dwa itd… 😕
Być może mam przyciężkie myślenie po ostatniej uczcie, gdzie głównym daniem, jakże by inaczej, była właśnie pieczona baranina.
Mam również uwagę co do zasad. Wiem, że należy powściągnąć zapędy powieściopisarzy (do których przez swój przydługi dowód sam się zaliczyłem) a szczególnie tych piszących w odcinkach ;-). Sądzę jednak, że zasady oceny dowodów można było ogłosić przed konkursem.
Powrócę na koniec do Maczka i proponuję rozważyć przypadek, gdzie liczba owiec – po zjedzeniu jednej – równa jest 127. Czy i tym razem wszystkie owce trafią w ręce jednego kułaka?
Pozdrawiam,
Jazz_off
Jazz_onie:
skoro po n-tym „transferze” owieczek ich liczba u wszystkich górali – oprócz jednego – dzieli się przez 2^n, a suma wszystkich owieczek także jest podzielna przez 2^n, to u tego jednego, ktoremu ubywa owieczek, także musi być przez 2^n podzielna.
Jeśli chodzi o sprawy formalne (pomoc losowi) – święta racja. Powinienem wspomnieć na poczatku zabawy o kryteriach oceny. Przepraszam autorów długich dowodów i obiecuje poprawę.
Pozdrav
mp
Pytanie na koncu postu Jazz_ona nie wydaje mi sie specjalnie ciekawe – to chyba od razu widac, ze taka sytuacja nie moze zajsc gdy liczba jest nieparzysta – zeby na koncu u jednego gorala byly wszystkie owce przed ostatnim rozkulaczeniem musza byc u dwoch gorali i to po rowno 🙂
Zagadnienie, ktore wydaje mi sie ciekawsze (aczkolwiek za dlugo sie nie zastanawialem, wiec moze odpowiedz jest podobnie trywialna 😉 ) jest: podaj uklad poczatkowy, w ktorym po dokladnie 7 rozkulaczeniach 127 owiec nie mozna juz wiecej rozkulaczac lub udowodnij, ze taki uklad poczatkowy nie jest mozliwy 🙂
Pozdrawiam,
Michal
Zgadzam się z Karwerem, że nie jest to specjalnie ciekawe pytanie. Miało ono na celu nakłonienie do rozważenie innych zakończeń (nie koniecznie w siedmiu krokach) np. przypadków … niekończącego się zorkułaczania jak m.in. dla rozkładu: 1, 126.
Oczywiście, cóż to za baca z jedną owcą (może to tylko kandydat na juhasa), ale nie o to tu chodzi.
Pytanie brzmi jak rozpoznać, który podział 127 owiec daje rozwiązanie w skończonej liczbie kroków i np. ile istnieje takich podziałów. Może odpowiedź jest trywialna – tego nie wiem.
Pozdrawiam,
Jazz_off
Panie Marku, czyżby Pan jako człowiek gór nie bywał nad morzem i nie widział nigdy dmuchanej piłki plażowej dla dzieci? 😉 Nie wiem jak teraz, ale dawno temu (jednak w czasach, które wcale nie najstarsi górale dobrze pamiętają 🙂 ) były one bardzo popularne – w różnokolorowe, biegnące południkowo „pasy”. Na nich było doskonale widać, że boki owych „pasów” schodzą się nie po prostej, a po łuku. Można to też zaobserwować spoglądając na siatką geograficzną na globusie.
Tak więc błąd tkwi w założeniu, że figura ABN jest trójkątem. Trzeba pamiętać choćby o tym, iż przy podstawie „odcinki” AN i BN są równoległe, zatem muszą się wyginać, aby móc się zbiec na biegunie.
Podaną metodą można obliczyć co najwyżej pole powierzchni bocznej stożka (choć na to jest akurat znacznie prostszy sposób).
Na razie tyle. Spróbuję później jeszcze trochę więcej napisać, ale nie wiem, czy zdążę przed piątkiem. Przyznaję się bez bicia, że dzisiaj pierwszeństwo przed Łamiblogiem ma mecz Polska-Austria.
Pozdrawiam
AB
piłki na euro 2012 opatentować, mniejsza o oszczędności na skórze, ale zwiększymy swoje szanse, choć ze słynnego powiedzenia trenera Górskiego pozostaną tylko 2 bramki