Były sobie świnki…
Dlaczego świnki? Po pierwsze dlatego, że według kalendarza chińskiego mamy rok świni, więc czemu by do tego nie nawiązać, zwłaszcza że do roku szczura już bliżej niż dalej. A po drugie…
Przeglądałem ostatnio książkę otrzymaną kilkanaście lat temu od znanego rosyjskiego „gołowołomszczika”, a z książki wypadł dodatkowy prezent, o którym nie pamiętałem – kartka-łamigłówka. Na kartce naszkicowana jest mapka WNP z pewnym tekstem. Po odpowiednim złożeniu mapka zmienia się w niepoprawny politycznie rysunek. Piszę enigmatycznie, ponieważ mimo upływu lat rysunek pozostaje niepoprawny, więc póki co szczegóły wypada przemilczeć. Natomiast zasada tej zginanki jest dokładnie taka sama, jak pewnej innej, również „politycznie zaangażowanej”, która pojawiła się w czasie II wojny światowej jako dodatek do jednego z czasopism amerykańskich.
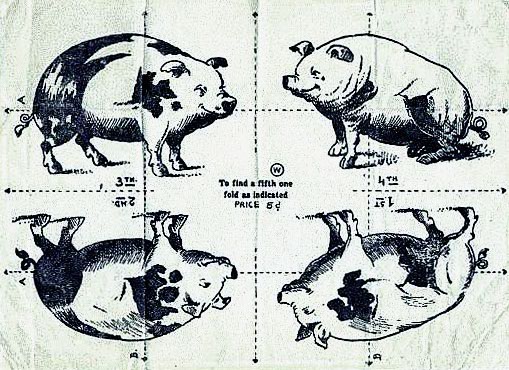
Pytanie brzmi: gdzie jest piąta świnia? Odpowiedź ukazuje się po sprytnym złożeniu kartki – wzdłuż zaznaczonych na rysunku linii przerywanych. Przerabiając nieco rysunek i umaszczenie trzody, można zmieniać rozwiązanie, którym w innych wersjach zginanki były pozostałe antypatyczne typy z ówczesnej zbrodniczej Osi.
Nie udało mi się niestety zdobyć współczesnej wersji z Saddamem Husajnem, wydanej podczas pierwszej wojny w Zatoce Perskiej.
Powyższa łamigłówka należy do bardzo nielicznych o charakterze propagandowym i chyba jest jedyną, w której świnki pojawiają się w złej konotacji. Na ogół te sympatyczne i mądre stworzenia bywają ozdobą zadań.
Do trzech świnek wrzucono sześć monet – trzy 5- i trzy 10-groszowe – tak, że w każdej znalazły się dwie monety.

Wiadomo, że w jednej śwince jest 10 groszy, w drugiej 15, a w trzeciej 20, jednak kwota napisana na żadnej nie odpowiada jej zawartości. Odwracając jedną ze świnek i potrząsając nią dotąd, aż wypadnie z niej tylko jedna moneta, można ustalić, jaka kwota znajduje się w każdej skarbonce. Którą świnką należałoby w tym celu potrząsać i dlaczego?
Swego czasu redaktor naczelna pewnego czasopisma zaskoczyła mnie następującą zagadką:
farmer ma trzy świnki różowe, cztery brązowe i jedną czarną; ile świnek może powiedzieć o sobie, że jest takiego samego koloru, jak jedna z jej koleżanek?
Nie domyśliłem się niestety, że to trywialne zadanie jest żartem i podałem… nieprawidłową odpowiedź.
A na deser dziewięć prosiaczków bez dodatkowych wyjaśnień.
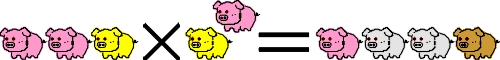
Czy rozwiązanie jest jedno?
PS w następnym wpisie zagadką z nagrodą.

Komentarze
Pierwsze zadanie – trzy świnki :
Obracamy i potrząsamy świnką z napisem 15 ;
– jeżeli wypadnie 5 groszy to znaczy , że w środku były dwie 5 groszówki
w śwince z napisem 20 nie może być ani 10 , ani 20 groszy czyli jest 15 groszy , a w ostatniej z napisem 10 jest groszy 20
– jeżeli wypadnie 10 groszy to znaczy , że w środku były dwie 10 groszówki , w śwince z napisem 10 nie może być ani 10 , ani 20 groszy czyli jest 15 groszy , a w ostatniej z napisem 20 jest groszy 10 .
logiczne
Drugie zadanie : żadna
Różowe świnki mogą powiedzieć , że są tego samego koloru jak dwie z ich koleżanek (nie wiem , czy między świnkami są prawdziwe koleżanki ? )
Brązowe świnki mogą powiedzieć , że są tego samego koloru jak trzy z ich koleżanek . A ta czarna bidula , że żadna nie jest tego samego koloru . A zatem żadna nie może powiedzieć , że „jedna” z jej koleżanek jest tego samego koloru . Taki semantyczny (jakie to słówko stało się popularne !) żart .
Przypominam: komentarzy z rozwiązaniami nie uwalniam ex tempore pro publico bono, lecz dopiero tuż przed następnym scriptum, czyli tym razem w Veneris.
Witam.
Rozwiązania zadań:
1. Trzy świnki-skarbonki.
Należy potrząsać świnką z napisem 15 (dlatego, że tylko w niej może być 5gr + 5 gr albo 10 gr + 10 gr).
W poszczególnych skarbonkach mogą się znajdować następujące zestawy monet:
a) świnka z napisem 10 – 5 gr + 10 gr albo 10 gr + 10 gr;
b) świnka z napisem 15 – 5 gr + 5 gr albo 10 gr + 10 gr;
c) świnka z napisem 20 – 5 gr + 5 gr albo 5 gr + 10 gr.
Jeśli ze świnki z napisem 15 wypadnie 5 gr, to jest w niej 10 gr, a to oznacza, że w śwince z napisem 10 jest 20 gr, a w śwince z napisem 20 – 15 gr. Jeśli natomiast wypadnie z niej 10 gr, to jest w niej 20 gr, w śwince z napisem 10 jest 15 gr, a w śwince z napisem 20 jest 10 gr.
2. Dziewięć różnokolorowych prosiaczków.
223 x 3^2 = 2007
Jest tylko jedno rozwiązanie (przy założeniu, że prosiaczkom o tym samym kolorze odpowiadają te same cyfry od 0 do 9, a zarazem różne dla każdego koloru).
3. Zginanka.
Po odpowiednim złożeniu kartki pojawia się twarz Adolfa Hitlera (piątej świni).
Pozdrawiam
Piotr
Zadanie ze świnkami-skarbonkami nie jest trudne:
Najpierw rozłożenie 6 monet:
świnka 1: dwie pięciogroszówki
świnka 2: dwie dziesięciogroszówki
świnka 3: jedna pięciogroszówka i jedna dziesięciogroszówka
Wyciągamy jedną monetę ze skarbonki oznaczonej cyfrą 15. Z warunków zadania wynika że muszą w niej być dwie jednakowe monety (abo dwie pięciogroszówki albo dwie 10-groszówki). Teraz rozważmy oba przypadki:
ze skarbonki wypadła 5-groszówka.
wnioskujemy ze w skarbonce znajduje sie 10 groszy. Tak więc do zidentyfikowania zostają skarbonki z napisem 10 oraz 20 przy czym znajduje się w nich albo 15 albo 20 groszy. Ponieważ w śwince z numerem 20 nie może być 20 groszy a zatem:
świnka z numerem 15 – 10 groszy
świnka z numerem 20 – 15 groszy
świnka z numerem 10 – 20 groszy
Teraz drugi przypadek: ze skarbonki wypadła 10-groszówka.
wnioskujemy ze w skarbonce znajduje sie 20 groszy. Tak więc do zidentyfikowania zostają skarbonki z napisem 10 oraz 20 przy czym znajduje się w niech albo 15 albo 10 groszy. Ponieważ w śwince z numerem 10 nie może być 10 groszy a zatem:
świnka z numerem 15 – 20 groszy
świnka z numerem 10 – 15 groszy
świnka z numerem 20 – 10 groszy
Trzy świnki:
Potrząsamy świnką z liczbą 15. Ponieważ nie może ona zawierać 5 i 10 gr, więc w środku pozostanie druga taka sama moneta jak ta, co wypadła. Pozostałe dwie już łatwo (bazując na informacji, że zawartość jest niezgodna z opisem).
Kolorowe świnki:
Nie jestem pewien, na czym miał polegać żart, więc strzelam, że zero (żadna ze świnek nie ma dokładnie jednej koleżanki w swoim kolorze).
Dziewięć prosiaczków:
Jeśli tylko zadanie nie ma jakiegoś „drugiego dna”, którego nie zauważyłem, to rozwiązanie jest jedno:
223 x 3^2 = 2007
(czyli otrzymujemy rok świni 😉 ).
Pozdrawiam
AB
Trzy świnki.
Należy odwrócić świnkę z liczbą 15. Mogą w niej być dwie monety pięciogroszowe, lub dwie dziesięciogroszowe. Jeśli wypadnie 5, to wiemy, że w śwince z 15 są dwie 5, w śwince z 10 muszą być dwie 10, a w trzeciej z 20 – 5 i 10. Jeżeli wypadnie 10, to w śwince z 15 są dwie 10, w śwince z 20 dwie 5 a w pozostałej 5 i 10.
Prosiaczki.
Wynik działania to 2007.
Pozdrawiam. e
świnie 1:
po pierwsze, rozkład musi być 10,15,20. łatwo to sobie uzmysłowić.
bierzemy świnię środkową, gdzie jest albo 10 albo 20 i wyjmujemy jedną monetę. jeśli jest to 5 to w świni jest 10 w p.p. 20. jeżeli 10 to po lewej jest 20 a po prawej 15. jeżeli 20 to odwrotnie
świnie 2:
jedno
Należy potrząsnąć świnką „15”.
1) Jeśli wypadnie 5-groszówka, to mamy:
w „10” dwie 10-groszówki
w „15” dwie 5-groszówki
w „20” jedną 5-groszówkę i jedną 10-groszówkę
2) Jeśli wypadnie 10-groszówka, to mamy:
w „10” jedną 5-groszówkę i jedną 10-groszówkę
w „15” dwie 10-groszówki
w „20” dwie 5-groszówki
Deser z prosiaczków: 223 x 3^2 = 2007
Pozdrawiam, Ola 😀
1) Świnka z 15 (z niej może wylecieć tylko 5 groszy co oznacza, że w niej jest 10 groszy lub dziesięć groszy – wówczas jest w niej 20 groszy).
Ponieważ są tylko dwa układy monet
1. 20 10 15
2. 15 20 10
jeżeli wypadnie pięć groszy to układ 1. w drugim przypadku 2.
2)Świnie nie mówią (choć nie wszystkie)
3)223*3^2=2007. Rozwiązanie jest jedno.
Antyp
za rozowa swinke podstawiamy 2, a za zolta 3 i wychodzi 2007 🙂 z komputerowych obliczen wyszlo mi ze rozwiazanie jest jedno. Oczywiscie rozumiem, ze swinki to liczby 0..9.
Zadanie z dziewięcioma prosiaczkami – znalazłem takie oto rozwiązanie:
223 * 3 do potęgi 2 = 2007
Wydaje mi się, że przy standardowych założeniach (świnkom o tym samym kolorze przyporządkowane są te same cyfry, świnkom w różnych kolorach – różne cyfry, ponadto liczby użyte w zadaniu nie mogą zaczynać sie od cyfry 0) zadanie ma tylko to jedno rozwiązanie.
Witam
Mogę zgodzić się, że niepoprawny politycznie rysunek wypada przemilczeć, ale polityka to niezbyt ciekawy świat, więc może wypadałoby pokazać rysunek.
Świnki skarbonki:
Środkowa świnka jest kluczem do prawdy o stanie posiadania wszystkich świnek. Szczegóły, wprawdzie nie wypada, ale przemilcze.
Farmer i jego świnki:
Jeśli zadanie jest żartem to potraktujmy problem poważnie i odpowiedzmy na pytanie: Czy świnki umieją mówić?
Trochę z innej beczki, ale w pewnym sensie podobne do powyższego zadania.
Pytanie stawiane studentom przez profesora Bronisława Knastera na jego wykładach z topologii (dział matematyki, a nie nauka o topolach):
„Czemu sułtan turecki nosi zielone szelki?”
Deser z dziewięciu prosiaczków:
Nasuwa się jedno rozwiązanie (pomysłowy wynik)
223*3^2=2007
Co do innych rozwiązań to … daltoniści mogą nimi sypać jak z rękawa.
Może specjaliści innych systemów liczbowych niż system dziesiętny mogliby coś znaleźć.
Pozdrawiam
W nadsyłanych komentarzach pojawiła się ciekawa sugestia dotycząca zadania z 9 prosiaczkami:
>Może specjaliści innych systemów liczbowych niż system dziesiętny mogliby coś znaleźć.< Moim zdaniem nie, ale głowy nie dam, czy w jakimś systemie "większym" niż dziesiętny nie dałoby się czegoś przypasować. Czy jakiś wytrawny łamigłówkowicz byłby w stanie rozstrzygnąć ten problem? mp
A no tak, o innych systemach liczbowych nie było mowy. Napisałem program, który znajduje rozwiązanie tego równania dla wszystkich systemów liczbowych od dwójkowego do podstawy 36. Niestety, jedyne rozwiązanie jest w systemie dziesiątkowym (to, o którym wspomniałem wcześniej – 2007).
Gdyby jednak nie zwrócić uwagi na to, iż ostatnia cyfra wyniku (brązowa świnka) musi być różna od pierwszej (różowej), wtedy rozwiązań jest wiącej, mianowicie:
w systemie o podstawie 3: różowa=1, żółta=2, wynik 1001
a gdyby jeszcze założyć, że różowa i żółta świnka mogą być takie same to:
– w systemie o podstawie 3: różowa=2, żółta=2, wynik 2220
– w systemie o podstawie 22: różowa=3, żółta=3, wynik 3IIF
– w systemie o podstawie 23: różowa=3, żółta=3, wynik 3FFC
– w systemie o podstawie 24: różowa=3, żółta=3, wynik 3CC9
– w systemie o podstawie 25: różowa=3, żółta=3, wynik 3996
– w systemie o podstawie 26: różowa=3, żółta=3, wynik 3663
– w systemie o podstawie 27: różowa=3, żółta=3, wynik 3330
Oczywiście zdaję sobie sprawę, że te rozwiązania nie spełniają warunków zadania, ale podałem je, bo może kogoś zainteresują.
Pozdrawiam,
Limak
p.s.: aa, nie wiem czy moje obliczenia są dobre, bo mogłem się gdzieś pomylić podczas programowania… wiadomo, późno już 😉
Po przeczytaniu sugestii z komentarza Pana Marka stwierdzam, że muszę skorygować moją odpowiedź na zadanie z prosiaczkami. Otóż jeśli uwzględnić systemy niedziesiętne to rozwiązań jest nieskończenie wiele. A ich postać jest następująca (oznaczam różowego prosiaczka jako a, żółtego – b, białego – c, brązowego – d, podstawę systemu – N):
a=k, b=k+1, c=0, d=(k+1)^k-k,
N=(k+1)^k+1
gdzie k jest dowolną liczbą całkowitą większą niż 1.
Np.:
Dla k=2 mamy rozwiązanie „dziesiętne”, które podałem już poprzednio.
Dla k=3 otrzymujemy:
334 x 4^3 = 300[61]
w systemie o podstawie 65
czyli: (3x65x65 + 3×65 + 4) x 4^3 = 823936 = 3x65x65x65 + 61.
Dla k=4:
445 x 5^4 = 400[621]
w systemie o podstawie 626
obie strony są równe wówczas 981258125.
Itd., itd… – rośnie niemiłosiernie szybko, ale działa 🙂
Uwaga: dla k=1 (system trójkowy) równość też jest spełniona, natomiast nie jest spełniony warunek, że różnym oznaczeniom odpowiadają różne cyfry (tzn. a=d=1).
Nie przeczę, że mogą istnieć również inne postacie rozwiązań, ale na pewno nie dla systemów o podstawie mniejszej niż 1000, bo tu sprawdziłem wszystkie możliwości.
Pozdrawiam
AB
Do Andrzeja:
Na topolach się nie znam 😉 , ale myślę, że sułtan nosi zielone szelki, aby mu spodnie nie spadły 🙂 .
Czy taka jest odpowiedź?
Pozdrawiam
AB
Do Limaka (i innych, których to interesuje 😉 ):
Używanie komputera do rozwiązywania „prosiaczków” w systemie dziesiętnym to przesada, ale w innych systemach to pewnie jedyne sensowne wyjście. Niepotrzebnie chyba tylko założyłeś ograniczenie podstawy do 36 (inna sprawa, że rozważanie wyższych zakrawa na maniactwo 😉 ). Być może chciałeś przy okazji uzyskać dużo innych informacji (co wnioskuję z tego co napisałeś w swoim komentarzu). Ja postawiłem na prostotę (z lenistwa), ale za to bez górnego limitu. Chodziło mi o to, by uzyskać możliwie dużo rozwiązań, bo chciałem poszukać zależności ogólnej.
Jeśli Cię to interesuje, to mogę Ci przysłać moje wypociny (oczywiście nic odkrywczego tam nie ma), napisane w Pascalu (Delphi 6) jako aplikacja konsolowa. Programiki są dwa. Pierwszy – ogólny – natychmiast wyłapuje dwa rozwiązania (tzn. dziesiętne i dla podstawy 65), na trzecie (pods. 626) trzeba krótką chwilę zaczekać, o następnym raczej nie ma mowy (może po miesiącu by było). Ale już te trzy rozwiązania pozwalają zauważyć wiele zależności (m.in. to, że żółty prosiaczek jest o 1 większy od różowego). To skłoniło mnie do małej modyfikacji (drugi programik), gdzie oparłem się na tym założeniu, a w zamian wyleciała jedna pętla. Dzięki temu uzyskałem czwarte rozwiązanie (dla pods. 7777) i korzystając z tego udało mi się sformułować wzór ogólny. Potem jeszcze tylko dowód (wbrew pozorom bardzo prosty!) i stąd wniosek, że uwzględniając systemy niedziesiętne to rozwiązań jest nieskończenie wiele.
Pozdrawiam
AB
P.S. Bloxorz 2? Jestem za!!! 🙂
Do Andrzeja69
TAK,taka jest odpowiedź.
Dlaczego taka odpowiedź?
Szczegóły można znaleźć na:
http://www.uz.zgora.pl/wydawnictwo/miesiecznik03-2005/05.pdf
Pozdrawiam
@Andrzej69:
Do systemu dziesietnego użyłem komputera aby mechanicznie się upewnić czy napewno niczego nie przegapiłem, ale może masz i racje, że to przesada.
Co do tego ograniczenia do 36 to po prostu z lenistwa, bo skorzystałem z gotowych funkcji konwersji liczb na inne podstawy liczbowe, a tutaj ograniczeniem bylo wlasnie 36 (0..9+a..z). Aplikacje napisalem w… PHP! może wiekszosci wyda się to dziwne, ale php również nadaje się do tego typu rzeczy i oczywiscie działa nie tylko w przegladarce ale pod konsolą rownież (po prostu na php sie „wychowalem” i szybciej mi sie w nim programuje niz w delphi/pascalu). Gdybym chcial uwzględnić systemy wieksze niz 36 musialbym po prostu napisac odpowiednie funkcje, a w nocy mi sie juz nie chcialo.. Zreszta teraz widze, ze komuś sie jednak chciało (masz racje, to graniczy z maniactwem 😉 ). Jak chcesz mozesz podesłac swoj programik, kamil at karczmarczyk com
pozdrawiam 🙂
p.s.: ładny wzor, gratuluję dogłebnej analizy i spostrzegawczości:)
Co do farmera i jego 8 swinek to jest przerobiona wersja zagadek szeherezady Raymonda Smullyana i odpowiedz zapewne brzmiala 8 (czarna moze sklamac) 🙂
Z innych takich zagadek to na przyklad
dwa wielbłądy są zwrócone w przeciwnych kierunkach. jeden stoi skierowany „twarza” na wschod a drugi na zachód. wielbłądy widzą siebie nawzajem bez odwracania się, a nawet bez obracania glowami, a poniewaz stoja na pustyni, zadne lustro itp nie sa dostepne. jak to możliwe?
a to tegoz samego autora do pokombinowania 😉 (jakkolwiek tez przerobiona troche)
Pewien Zwykły Ktoś zakochał się w córce sułtana jo3 i poprosił go o jej rękę.
-moja córka jest bardzo wybredna – odpowiedział srogo sułtan jo3 – i chce wyjść za mąż tylko za kogoś o wyjątkowej inteligencji. Jesli chcesz ją poślubić, musisz najpierw przejść sprawdzian.
-jaki sprawdzian? – spytał Zwykły Ktoś.
-musisz napisać liczbę, którą wyślesz Księżniczce Biedronie. Ona odesli ci jakas inna liczbe. Jesli liczba, którą otrzymasz z powrotem bedzie taka sama jak ta, ktora wyslales, bedziesz mogl przejsc do nastepnej proby. Jezeli liczby beda rozne, przestaniesz sie liczyc jako kandydat do ręki Księżniczki Biedrony.
-Ale jaką liczbę mam napisać? – spytał Zwykły Ktoś – skąd mam wiedzieć jaka liczba przyjdzie księżniczce do glowy?
-Liczba, ktora odesle ci ksiezniczka – odparł sułtan jo3 – nie bedzie zupelnie przypadkowa. bedzie zalezala od liczby, ktora ty jej przeslesz. Dokladniej mowiac, liczba ktora wyslesz ksiezniczce, jednoznacznie okresla, jaka liczbe dostaniesz z powrotem. jesli wiec wybierzesz odpowiednia liczbe, ksiezniczka odesle ci taką samą.
-Dalej nie wiem, jak mam odgadnąć, jaką liczbę wysłac.
-To nie polega na zgadywaniu – odrzekł sułtan. – powinienes wydedukowac wlasciwa liczbe z regul, ktore zaraz ci podam. Dla dowolnych dwoch liczb x i y jako xy oznacze nie ich iloczyn, ale polaczenie liczb w jedna. Np. jesli x=5079, a y=863, to xy=5079863. A oto reguły:
REGUŁA 1
dla kazdej liczby x, jezeli napiszesz 1×2, ksiezniczka odesle ci liczbe x. Np. jesli napiszesz 13542, to otrzymasz z powrotem 354.
REGUŁA 2
dla kazdej liczby x powtorzenie to xx. Np. powtorzeniem liczby 692 jest liczba 692692. druga reguła mówi, że jesli x zwraca liczbe y, wowczas 3x (nie mnozenie) zwraca powtorzenie liczby y. Np. 15432 zwraca liczbe 543, wiec 315432 zwraca liczbe 543543. wynika stad takze, ze jesli wyslesz liczbe 3315432, to otrzymasz z powrotem 543543543543 (poniewaz 315432 zwraca liczbe 543543).
REGULA 3
przez odwrocenie liczby rozumiem liczbe zapisana wstecz. np odwroceniem liczby 62985 jest 58926. Trzecia regula mowi, ze jesli x zwraca liczbe y, wowczas 4x (znow nie mnozenie, tylko dostawienie cyfry 4 przed liczbe x) 4x zwraca odwrocenie liczby y. np poniewaz 172962 zwraca liczbe 7296, zatem 4172962 zwraca liczbe 6927. jesli poslesz Ksiezniczce Biedronie liczbe 4172962, ona odesle ci 6927. Albo, laczac reguly 1,2 i 3 – 316982 zwraca liczbe 698698 (korzystajac z regul 1 i 2), wiec 4316982 zwraca liczbe 896896.
REGULA 4
regula usuwania. jesli x zwraca liczbe y, ktora ma co najmniej dwie cyfry, wowczas 5x (pamietaj, nie mnozenie, tylko dostawienie cyfry) 5x zwraca y z usunieta pierwsza cyfra. np 13472 zwraca 347, wiec 513472 zwraca liczbe 47.
REGULA 5
regula dodawania. jesli x zwraca liczbe y, wowczas 6x (pamietasz na pewno 🙂 ) 6x zwraca liczbe 1y a 7x zwraca 2y (to też nie mnozenie, tylko dostawienie cyfry 1 i 2). na przyklad 15832 zwraca 583, zatem 615832 zwraca 1583, a 715832 zwraca 2583.
Takie sa reguly – powiedzial sultan jo3. sprobuj znalezc teraz taka liczbe x, ze jesli wyslesz ja Ksiezniczce Biedronie, otrzymasz z powrotem taka sama liczbe x.
istnieje nieskonczenie wiele rozwiazan, ale wystarczy znalezc jedno.