Jeden warunek

3 sierpnia 2007
Marek Penszko

Myszkuję od czasu do czasu po Internecie, szukając nowości i ciekawostek ze świata sudoku. Poluję głównie się na oryginalne, pomysłowe odmiany tej łamigłówki. W minionym półroczu znalazłem ich niewiele i żadna mną nie „wstrząsnęła”. Pojawia się natomiast sporo ekstrawagancji, które toleruję oraz żartów w rodzaju sudoku piwnego (a propos ubiegłorocznego turnieju sponsorowanego przez japońską firmę piwowarską Asahi).

Piw_d.jpg

Natomiast serio skłaniam się ostatnio ku temu, co nazwałbym pozorną klasyką. Pozorną, ponieważ diagram prawie niczym nie różni się od zwykłego sudoku, czyli nie ma w nim żadnych dodatkowych oznaczeń, które sugerowałyby, że coś jest nie tak. Gdyby jednak, niczego nie podejrzewając, uznać zadanie za tradycyjne, nie zerknąwszy uprzednio do instrukcji, to z reguły dałoby się wpisać ledwie kilka cyfr albo żadnej. Oto przykład:

War_1.jpg

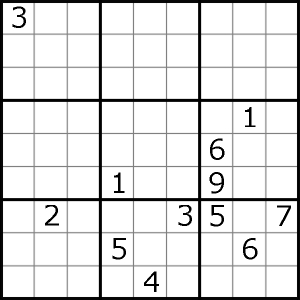
W tym i wielu podobnych diagramach-pozorantach łatwo zauważyć, że cyfr jest zdecydowanie za mało jak na zwykłe zadanie. Dlatego napisałem, że diagram nie różni się „prawie” niczym od klasyki, bo jedyną dostrzegalną natychmiast różnicą bywa rzekomy niedostatek cyfr.
Jak wiadomo w tradycyjnym sudoku cyfr powinno być przynajmniej 17 – to najprawdopodobniej jeden z warunków koniecznych, aby było dokładnie jedno rozwiązanie. Ta siedemnastka od prawie dwóch lat spędza matematykom sen z powiek, bo jak dotąd nikomu nie udało się udowodnić, że właśnie tyle stanowi minimum albo nie stanowi. Próby trwają, więc tylko patrzeć, jak ktoś na przykład zrobi doktorat z sudoku. A może już są tacy.

Wracając do przykładu, cały smaczek takich i podobnych quasi-klasycznych zadań polega na dodaniu jakiegoś eleganckiego warunku – zwięzłego i oryginalnego – który, nie komplikując rozwiązywania, urozmaica je i uatrakcyjnia.
W powyższym przykładzie warunek jest nienowy: cyfry w sąsiednich polach nie mogą być kolejnymi, czyli różniącymi się o jeden. Nazwałem kiedyś takie sudoku NPK (Nie Po Kolei), ale niezbyt mi się widzi takie skrótowe określenie. Może uda się znaleźć lepsze. Po angielsku to „non-consecutive” – też nieszczególne i przydługie.

Takich z wyglądu na pozór klasycznych odmian sudoku jest niewiele. Można by zaliczyć do nich sudoku X, bo o przekątnych nietrudno pamiętać w trakcie rozwiązywania, więc nie trzeba ich koniecznie zaznaczać. Inny pomysł prezentowałem dawno temu w Łamiblogu. Chodzi o sudoku konno, które okazało się polskim produktem eksportowym i trafiło na kilka stron obcojęzycznych, między innymi na hiszpańską jako anti-caballo.

Wymyślaniem nowych wariantów zabawiają się nasi najlepsi solwerzy. Kilka propozycji otrzymałem ostatnio od Janka Mrozowskiego z Krakowa, który w ubiegłym roku w Londynie został wicemistrzem świata w wersji interaktywnej, w bieżącym – mistrzem i międzynarodowym mistrzem Polski, a w 2. Mistrzostwach Świata w Pradze był 17 (tuż przed Janą Tylovą, mistrzynią świata z 2006 roku).
Jeden z jego pomysłów, właśnie taki pozornie klasyczny, bardzo mi się spodobał. Oto przykładowe zadanie:

War_2.jpg

Ile cyfr udałoby się z marszu, czyli bez próbowania i błądzenia, wpisać do diagramu, gdyby było to klasyczne sudoku? Dokładnie trzy (jeśli czegoś nie przegapiłem), a zadanie miałoby, bagatela, 557 rozwiązań. Jak zatem brzmi prosty i sprytny warunek dodatkowy, pozwalający wyłuskać z setek rozwiązań to jedyne?
Początkowo zamierzałem zrobić konkurencję wicehrabiemu Moncktonowi i potraktować to pytanie jako konkursowe z milionem dolarów nagrody. Jednak sponsor w ostatniej chwili się wycofał (żarty żartami, ale byłoby to zapewne horrendalnie trudne zadanie), zatem proponuję bezinteresowną zabawę polegającą na uzupełnieniu zdania stanowiącego wspomniany warunek:
W żadnym ____ ____ wszystkie cyfry nie mogą być ____ ani ____.
Zamiast kresek należy wstawić właściwe wyrazy, choć jeden z nich w gruncie rzeczy trudno nazwać wyrazem (ta informacja może stanowić podpowiedź) – a potem przystąpić do rozwiązywania, przestrzegając rozszyfrowanego warunku. Satysfakcja gwarantowana, bo do celu dochodzi się przyjemnie, choć niełatwo, ale z „momentami”. Wyjaśniam, że „moment” to bardzo miłe, niespodziewane odnalezienie kolejnego tropu po krótkiej lub dłuższej chwili zagubienia w gąszczu cyfr.
„Momenty były?” – czy ktoś jeszcze pamięta skąd to pytanie?

Jeśli w komentarzach pojawią się propozycje warunku dodatkowego, będę naprowadzał na właściwy lub potwierdzę jego poprawność, gdy ktoś trafi w sedno.