Finał
W kilku ostatnich wpisach prezentowałem wybrane zadania z 15 Mistrzostw Świata w Rozwiązywaniu Łamigłówek. Na zakończenie tego wątku jeszcze trzy ciekawe, choć niełatwe przykłady z rundy finałowej.
Finał, jako odrębny, specyficzny etap mistrzostw, wprowadzili Amerykanie w 2000 roku w celu uatrakcyjnienia imprezy – uczynienia jej widowiskową, a samych zmagań bardziej emocjonującymi. Zwykle uczestniczy w nim czołowa dziesiątka z klasyfikacji utworzonej w wyniku poprzednich etapów, zaś wyniki finału rozstrzygają o kolejności w ramach tej dziesiątki. Może się więc zdarzyć, że osoba zajmująca dotychczas dziesiąte miejsce zostanie mistrzem świata.
Finaliści pojawiają się na scenie w światłach jupiterów i błyskach fleszów, zamieniają małe kartki na wielkie arkusze z diagramami zadań przypięte do stojaków, a długopisy na flamastry i dopingowani przez liczną widownię przystępują do zmagań. Na podpowiedzi nie liczą, bo umiejętnościami przewyższają obserwatorów, którzy zwykle mogą się tylko zachwycać sprawnością ich umysłów i szybkimi ruchami dłoni. Z reguły są też odporni na wszelkie hałasy, zwłaszcza szmery podziwu. Skupieni nad łamigłówkami praktycznie odcinają się od świata zewnętrznego. Nawet jeśli widz zauważy coś wcześniej, bo z reguły tok rozwiązywania nie jest ściśle określony, nie odważy się złamać zasady fair play. Co najwyżej szeptem podzieli się z sąsiadem uwagą w rodzaju: „piątka z prawej strony trzynastki” lub „druga litera C w najniższym polu” albo „linia między piątką a dwójką”. Być może takie ciche podpowiedzi padały w trakcie rozwiązywania na finale trzech poniższych zadań.
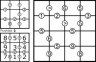
Szesnastka
Wpisz w pola liczby od 1 do 16 (w przykładzie do 9) tak, aby każda cyfra w kółeczku określała różnicę między parą liczb, między którymi się znajduje, a znak – zależność między tymi dwiema liczbami.
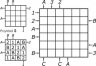
Początki
W każdy rząd pól należy wpisać trzy cyfry – 1, 2, 3 i trzy litery – A, B, C (w przykładzie po dwie – 1, 2 i A, B). Kluczem do ich właściwego rozmieszczenia są „podpowiedzi” znajdujące się przy brzegu – każda w miejscu, z którego patrząc zgodnie ze wskazaniem strzałki, widać:
– jako pierwszą literę tę, która znajduje się przy strzałce,
– tyle cyfr, jaka liczba jest przy strzałce – jeśli wiadomo, że większa cyfra zasłania mniejszą.
Cyfry i litery nie zasłaniają się wzajemnie.
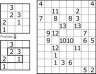
Cięcie liczbami
Podziel diagram wzdłuż linii przerywanych na dwie części o takim samym kształcie i wielkości. W każdej części powinno znaleźć się trzynaście różnych liczb (w przykładzie trzy).

Komentarze
Gdzie można znaleźć inne przykłady z 15 Mistrzostw w Rozwiązywaniu Łamigłówek.
Zadania z WPC nie są ogólnodostępne. Dysponują nimi (poza organizatorami i uczestnikami mistrzostw) tylko przedstawiciele organizacji należących do WPF, którzy z tytułu tej przynależności mają (ograniczone) prawo do ich publikacji. Na tej zasadzie pojawiło się kilka zadań w Łamiblogu, kilka innych znajdzie się w styczniowej „Wiedzy i Życiu”. W przygotowaniu jest książka z wyborem najciekawszych zadań z dotychczasowych mistrzostw świata.
Podoba mi się trzecie zadanie, ale nie podoba mi się, że środek nie jest jednoznaczny – otrzymuje się dwie dzielące linie.
W Początkach chyba powinno być nie „1,2 i 1,B” a „1,2 i A,B”
Dziękuję Pani Anko. Literówkę poprawiłem. O drugim rozwiązaniu „Cięcia liczbami” nic nie wiem (chyba nie „wypłynęło” ono na Mistrzostwach, a w każdym razie informacja o tym do mnie nie dotarła), a chętnie bym się jakoś dowiedział.
„Początki” są całkiem fajne . Przydaje się trening na zwykłej literamie , ale rozwiązuje się podobnie. Trzeba tylko ustalić sobie sekwencje liczb dla poszczególnych podpowiedzi i jeden raz wykluczyć wariant prowadzący do sprzeczności . Widziałem trudniejsze klasyczne literamy , ale to zadanie jest oryginalne i świeże przez swą modyfikację.
Początki są skrzyżowaniem Literami z Blokowiskiem. Ale typowy dla Blokowiska opis został zmodyfikowany i ograniczony do warunku, że większa cyfra zasłania mniejszą. I bardzo słusznie, w przeciwnym wypadku opis byłby zbyt długi i zagmatwany.
Dla „szesnastki” znalazłem dokładnie jedno rozwiązanie. Z braku lepszego pomysłu sprawdziłem wszystkie możliwe warianty dziewięcioliczbowego ciągu , a następnie dopasowywałem możliwe ciągi sześcioliczbowe. Ostatnia liczba wychodzi sama . Ogólnie rzecz biorąc , była to żmudna robota . Albo jest jakiś sprytniejszy sposób , albo trzeba mieć mózg arcymistrza szachowego. Albo jedno i drugie . Powodzenia
Przepraszam za zamieszanie. Rzeczywiście i ja w końcu mam jedno rozwiązanie, a poprzednia uwaga wzięła się z przeoczenia, że obydwie trójki wylądowały w jednej części.
Z badaniem wszystkich ciągów robota chyba była dość żmudna, ja do problemu podeszłam inaczej. Skoro mają w wyniku powstać dwie przystające figury, to muszą one być w prostokącie ulokowane symetrycznie względem środka. Ponieważ kilka jest natychmiastowych podpowiedzi, wystarczy dorysować symetryczne kreseczki, potem już uzupełniając linię, ani na chwilę o symetrii nie zapomnieć.
Pozdrawiam wszystkich.
Brawa dla Anki. Dobrze , że do problemu podeszłaś inaczej , bo moja wskazówka dotyczyła innego zadania i dla „cięcia liczbami” byłaby może nie tyle żmudna , co bezcelowa.