Para komplementarna
Nawróciłem się na krótko na Masterminda. Próbowałem ułożyć nieco dziwne zadanie. O szczegółach za chwilę, a tymczasem efekt moich prób – nie w pełni udany.
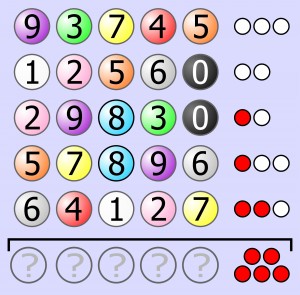
Zadanie polega na odgadnięciu kodu utworzonego z pięciu różnych cyfr. Kluczem do tego jest kilka podanych prób odgadnięcia i ocena zgodności każdej próby z kodem. Ocenę stanowią białe i czerwone kółeczka. Białe oznacza, że w próbie jest właściwa cyfra (taka jak w kodzie), ale umieszczona na niewłaściwym kolejnym miejscu; czerwone to pełna zgodność, czyli dobra cyfra na tym samym miejscu co w kodzie.
Na pozór jest to typowe mastermindowe zadanie w prostszej wersji (bez możliwych powtórek cyfr w kodzie). Istotne są jednak niecne intencje, jakie przyświecały jego układaniu. Otóż chodziło o to, aby miało ono dwa całkiem różne rozwiązania, czyli żadna cyfra kodu stanowiącego jedno rozwiązanie nie powinna występować w kodzie będącym drugim rozwiązaniem.
Kto rozwiąże, przekona się, że byłem bliski celu. A może komuś uda się osiągnąć taki cel, modyfikując to zadanie albo układając własne dziełko. Powinien być w nim jednak spełniony – aby były dwa kompletnie różne rozwiązania – pewien podstawowy warunek (jaki?), który w powyższym zadaniu został kompletnie i to, rzec można, trzykrotnie… zignorowany.

Komentarze
67139
Niestety nic więcej nie zauważyłem.
Pozwolę sobie udowodnić, że nie da się osiągnąć postawionego celu.
Załóżmy bowiem, że ułożyliśmy zadanie, które posiada dwa rozwiązania składające się z kompletu wszystkich 10 cyfr. Bez straty ogólności przyjmijmy, że tymi rozwiązaniami są sekwencje 01234 oraz 56789. Niech teraz pierwsza próba odgadnięcia sekwencji ABCDE zawiera x kółeczek (w sumie białych i czerwonych) jako ocena zgodności.
To oznacza, że zbiór {A,B,C,D,E} zawiera dokładnie x cyfr z zakresu 0-4 oraz dokładnie x cyfr z zakresu 5-9. Zatem cały zbiór {A,B,C,D,E} zawiera w sumie 2x cyfr z zakresu 0-9. Sprzeczność, bo tych cyfr jest dokładnie 5, natomiast 2x jest liczbą parzystą. To oczywiście potwierdza, że porywamy się z motyką na słońce.
Osobiście widzę 2 sposoby obejścia tego problemu:
– zmiana rozmiaru zadania tak, aby kod miał długość parzystą (np. kod o długości 4 cyfr ze zbioru 8-elementowego np. z zakresu 1-8),
– dopuszczenie w próbach odgadnięcia kodu strzałów z powtórzonymi cyframi. (np. strzał 34456 daje dwa kółeczka białe dla każdego z kodów 01234 i 56789
Panie Marku, które podejście obrać w dalszej zabawie z zadaniem?
Mam wątpliwości, jeśli chodzi o dowód, ale na razie pozostawiam sprawę otwartą.
Proponuję podejście z wszystkimi cyframi, czyli z powtórkami.
mp
Rozwiązania podanego zadania (brakuje cyfry 0, podwójnie występuje 7):
45827
67139
Dwa rozwiązania:
67139
45827
Zignorowany warunek, to oczywiście trzy kropy w podpowiedziach. Skoro mają być różne cyfry w obu rozwiązaniach, to taka sytuacja nie może się wydarzyć.
Taki wniosek na szybko (bo w pracy jestem).
Żeby były zupełnie 2 rozłączne zbiory rozwiązań, to w podpowiedziach mogłyby być maksymalnie 2 kropki, ponieważ 3 oznaczają, że conajmniej jedna liczba jest na pewno w obu rozwiązaniach. Skoro Gospodarz pisze, że mu sie prawie udało, to zakładam, że choć jedna liczba sie powtarza (co sugerują układy z trzema kropkami w podpowiedziach).
Mamy 3 takie układy, a we wszystkich powtarza sie liczba ‚7’……. 🙂
wnioski c.d.
wykreslajac ‚7’ z wierszy, mamy po 2 kropki podpowiedzi w kazdym, a wiec kazdy wiersz ma po 2 pary liczb z obu rozwiazan, szczegolnie w wierszach z wykresloną siódemką.
Kombinacji 5 nad 2 jest 10, a że są to pary to skraca sie nam do 5 (co widać w zadaniu, bo mamy 5 wierszy). A więc kazdy wiersz zawiera parę z danego rozwiązania, która sie nie powtarza w innym wierszu. Biorąc na tapetę pierwszy wiersz 9,3,4,5 (bez 7), dla ‚9’ tylko para 9,4 sie nie powtarza w żadnym innym. A więc 2 zbiory rozwiązań powiększyły sie nam o dwie liczby: 7,9,4 i drugi 7,3,5.
Następny wpis to będzie juz rozwiązanie… więcej w pracy nie mam czasu, a i tutaj nie chcę juz spamować. Mam tylko nadzieję, że wnioski wyciągam dobre 🙂
@miodziu: ja mam inny dowód, że się nie da.
Żeby zbiory były rozłączne czyli dwie grupy po 5 liczb, to w zadaniu nie może być więcej niz dwa kółka podpowiedzi. Trzecie kółko podpowiedzi oznacza, że ta 3 liczba wystepuje w obu rozwiązaniach. Więc… jedna podpowiedź może/musi zawierać dwie pary liczb, jedna para należy do jednego rozwiązania, druga do drugiego. To są 4 liczby. Wiersz podpowiedzi zawiera 5 liczb, czyli trzeba dodać jakąś piątą, która nie należałąby do żadnego zbioru rozwiązań, co jest niemożliwe: 5+5=10, nie mamy więcej wolnych liczb nienależących do żadnego rozwiązania, jakaś musi się powtarzać a w tym wypadku jakaś inna nie wystepuje wogóle w żadnym rozwiązaniu (ponieważ są wiersze z tylko dwoma kółkami)!
Wnioski:
1. w rozwiązaniach z tego zadania jest jedna liczba powtarzająca się i jedna niewystepująca (4+1+4=9).
2. jeśliby występowały wszystkie liczby w rozwiązaniach, to nie byłoby wiersza podpowiedzi z dwoma kółkami.
P.S. ewidentnie widać, że w wierszach z dwoma kółkami musi powtarzać się liczba, która nie występuje w rozwiązaniach, natomiast w wierszach z trzema kółkami, musi powtarzać sie liczba, która występuje w obu rozwiązaniach.
Dowód jest poprawny, ale w treści zadania nie ma zakazu zapytań z powtórzeniami, więc dowód dowodzi niemożności rozwiązania czegoś, co byłoby trochę innym zadaniem.
Naturalne wydaje się założenie, że odgadujący może testować dowolny zestaw cyfr – czyli także z powtórzeniami.
Oczywiście pamiętamy, że dwa szukane rozwiązania powtórzeń nie zawierają.
Otóż to 🙂
mp
45827 albo 67139
ale nie wiem, czy to jedyne rozwiązania
Co do trzykrotnie zignorowanego warunku, to chciałem napisać, że chodzi o warunek, że w takim zadaniu nie może być w żadnej linii więcej niż 2 kropki, ale jak przeczytałem, co napisał miodziu to trudno się z nim nie zgodzić: gdyby w rozwiązaniu miało nie być powtórek i w żadnej z podpowiedzi nie ma powtórzonych cyfr to nie jest możliwe stworzenie zadania z dwoma różnymi rozwiązaniami (np. 01234 i 56789)
Ok, rozwiązania :
67139
45827
Wiedząc, że jest 7 i nie ma 0,znalezienie pozostałych liczb jest trywialne , pozostaje tylko je ułożyć.
Zadanie mamy dość enigmatyczne, więc napiszę enigmatycznie, że siódemka jest w nim niezbyt szczęśliwa.
Te dwa rozwiązania to 45827 i 67139. Powtarza się 7. Gdyby każda cyfra pierwszego zestawu miała być inna od każdej cyfry drugiego zestawu, nie mogłyby jako kod trzy kółka- trzy poprawne w pierwszym zestawie, to dwie poprawne w drugim
Moja propozycja:
11089
43624
57729
57644
53023
W subtelności się nie bawiłem, więc każdy wiersz dostał taką samą ocenę: dwie czerwone kropy, żadnej białej.
patrząc już na pierwszą próbę odgadnięcia kodu wynikałoby, że w obu „różnych” rozwiązaniach występują trzy cyfry spośród pięciu: 34579 (kolejność pomijam) czyli co najmniej jedna cyfra powtarza się w obu tychże różnych rozwiązaniach.
Co do legalności zapytań z powtórzeniami, to nie mam zdania.
Bo z jednej strony nie jest powiedziane wprost, że tak nie można robić.
A z drugiej strony „Kluczem do tego jest kilka podanych prób odgadnięcia” – co niejawnie wyklucza zapytania z powtórzeniami, bowiem takie zapytanie nie mogą być „próbą odgadnięcia”, bo nie spełniają reguł prawidłowego kodu.
Oczywiście problem leży w precyzyjności sformułowań i wszelkie wątpliwości powinny być wyjaśniane. Bo język naturalny może być różnorodnie interpretowany, a w matematyce nie ma na to miejsca.
Tak dla rozluźnienia atmosfery podaję dwa zadanka, z dwoma rozłącznymi rozwiązaniami:
00009 10
06280 20
54734 20
80601 02
00009 10
06280 20
54734 20
60774 11
Oczywiście racja, zwłaszcza że dopuszczając powtórki w „strzałach” wypadałoby doprecyzować, na czym polega w takim przypadku ocena.
Przyznam się, że moja wątpliwość dotycząca dowodu była „prowokacją”, aby skłonić do wypowiedzi inne osoby :).
mp
@ y-b
53689
17024
@ miodziu
01234
56789
dla obu zadanek 😉
W zadaniach obu autorów jest według mnie dobra reguła dotycząca oceny powtarzających się cyfr:
– dany kolor/wartość cyfrową oceniamy tylko jeden raz w kolejności: czerwone kółko albo białe kółko.
Taka reguła jest powszechnie stosowana, ale gwoli ścisłości zawsze warto ją przypominać.
mp
Zadanko
3,7,8,9,8 02
7,8,4,7,2 02
0,3,0,9,7 11
0,2,3,2,9 20
1,9,6,5,9 20
A przy okazji nadmieniam, że moje zadanie , które umieściłem we wpisie „Po strzałkach” dostarcza rozwiązującemu wielu niezapomnianych doznań.
Domyślam się, że kilka osób miało z nim kontakt- dodam: to jest wyzwanie dla prawdziwego konesera 😉
Da się.
67139, nigdy nie byłem specjalnym mastermindowiczem, trochę na piechotę to rozwiązałem, ale chyba się zgadza.
I jeszcze drugie rozwiązanie by się przydało – ale to już pestka.
mp
Zabrałem się za to zadanie rzutem na taśmę i przyznam, że nie zrozumiałem przesłania, iż rozwiązania są dwa. Słowa o „bliskości celu”, a więc de facto jego niezrealizowaniu, zrozumiałem właśnie jako potwierdzenie, że udało się tylko jedno rozwiązanie, którego znalezienie było dla mnie pierwszą częścią zadania, a dalsze rozważania częścią drugą. Pomyślałem więc, że chociaż do tej pierwszej części dam odpowiedź 🙂