Powrót ołówków

7 sierpnia 2010
Marek Penszko

Trzy wpisy temu padło pytanie:
jak rozmieścić sześć ołówków, aby każdy dotykał pięciu (albo inaczej: aby stykały się każde dwa)?
Tuż po nim było drugie:
jak rozmieścić siedem ołówków, aby każdy dotykał sześciu?
Warto uściślić, że ołówki są po to, aby zadanie „trafiło pod strzechy” – w domyśle chodzi o walce.

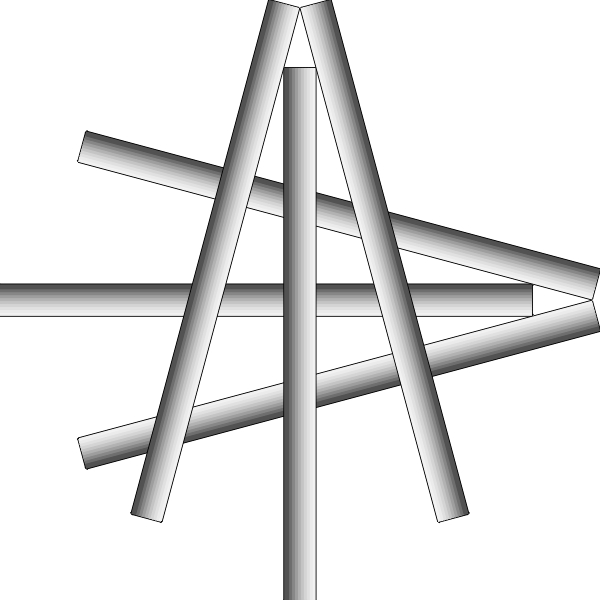
Miłośnikom matematyki rekreacyjnej znana jest odpowiedź na pierwsze pytanie, rzec by można, Gardnerowska, czyli układ taki, jak na poniższym rysunku, zamieszczony w Scientific American w 1957 roku (ale znany wcześniej), a potem pojawiający się w książkach Martina Gardnera.

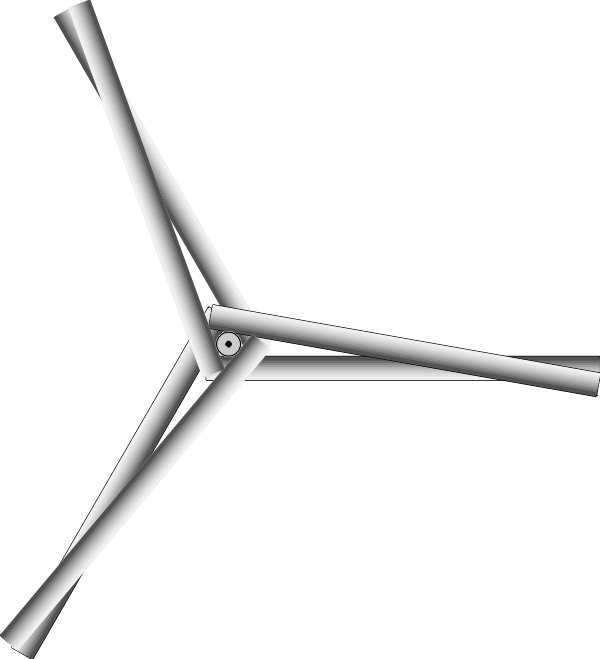
Gardnerowską można nazwać także odpowiedź na drugie pytanie, która była nowością nadesłaną wówczas przez kilkunastu czytelników:

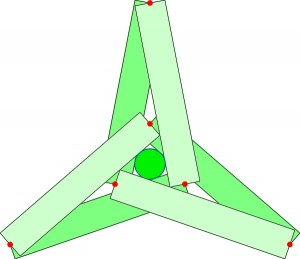
Warto zauważyć, że obie konstrukcje nie są bezwarunkowe. Jeśli założymy, że grubość walców jest jednakowa,  to ich długość (także jednakowa) będzie w obu przypadkach ograniczona z dołu. Dla sześciu walców powinna być mniej więcej 5-krotnie większa od grubości (dokładnej wielokrotności nie znam); dla siedmiu – przynajmniej 7/2*sqrt3 razy większa. Kluczowe znaczenie mają oczywiście punkty styku walców, leżących w dwóch warstwach. Trudno narysować „przełomowy” układ sześciu walców, łatwiej siedmiu:

Po minimalnym skróceniu walców wewnętrzne lub zewnętrzne punkty styku, oznaczone czerwonymi kropkami, „rozjadą się”.

Dla sześciu walców Gardnerowski układ nie jest jedynym rozwiązaniem. W roku 1968 angielski matematyk John Edensor Littlewood „poprawił” zadanie, pytając o największą liczbę jednakowych walców, ale nieskończonych, stykających się każdy z każdym. Inaczej mówiąc, chodzi o ołówki o długości obustronnie nieograniczonej, czyli powierzchnie walcowe (walce nie mają podstaw, a zatem punkty styku mogą być tylko na powierzchniach bocznych). Problem ma kilka rozwiązań dla sześciu walców i wszystkie one są oczywiście także rozwiązaniami dla „skończonych” ołówków. Co ciekawe, jest wśród nich rozwiązanie, które ma jeden stopień swobody, a to sugeruje, że możliwe byłoby „totalne sparowanie” także siedmiu powierzchni walcowych. Niestety, dotąd nikomu się to nie udało. Znany jest dowód ograniczający liczbę walców w układzie, z którego wynika, że nie może ich być więcej niż… 24. Tak wysoko umieszczona poprzeczka świadczy o trudności dowodzenia na styku geometrii, kombinatoryki i topologii.

Wróćmy do ołówków skończonych.
Zapewne przed laty Martin Gardner oniemiałby z wrażenia, gdyby jakiś czytelnik nadesłał rysunek ośmiu ołówków ułożonych tak, że każdy dotykałby siedmiu pozostałych. Jest to bowiem możliwe i wcale nie takie trudne, jeśli pamiętać, że konstrukcje nie są bezwarunkowe. Mówiąc wprost, w tym przypadku długości ołówków nie będą jednakowe, choć różniące się nieznacznie.
Czy ktoś z Państwa poradzi sobie z ósemką?

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.