Przez 7

Cecha podzielności przez 7 w polskiej Wikipedii brzmi tak:

Liczba jest podzielna przez 7, jeśli suma jej cyfr mnożonych (od prawej) przez kolejne potęgi 3 (włącznie z potęgą zerową: 3⁰=1) jest podzielna przez 7.

Od lat szkolnych wydawało mi się, że cechy podzielności są po to, abym mógł w prosty sposób sprawdzić, czy duże a jest wielokrotnością małego b. Tymczasem cytowana powyżej cecha wymaga bardziej skomplikowanych obliczeń, niż podzielenie a przez b.
Wygląda na to, że niektóre cechy podzielności to raczej łamigłówki, czyli są po to, aby próbować rozgryzać mechanizm ich działania albo je wymyślać.
Przypomnę kilka innych siódemkowych cech podzielności.

Liczba jest podzielna przez 7, jeśli przez 7 dzieli się…:

a) …suma algebraiczna liczb, które powstaną po pogrupowaniu trójkami (zaczynając od prawej) cyfr w testowanej liczbie i poprzedzeniu grup-liczb znakami „+” i „-” umieszczonymi na przemian.
Przykład:
2547034 -> -2 + 547 – 034 -> 511

b) …suma iloczynów kolejnych cyfr (zaczynając od prawej) i kolejnych cyfr tworzących cykliczny ciąg: 1, 3, 2, 6, 4, 5… (jeżeli liczba jest ponad 6-cyfrowa, cykl się powtarza).
Przykład:
25389154 -> 4*1 + 5*3 + 1*2 + 9*6 + 8*4 + 3*5 + 5*1 + 2*3 -> 133.

c) …wynik następującego ciągu działań:
– pomnóż pierwszą cyfrę przez 3, dodaj drugą cyfrę i podziel przez 7;
– resztę z dzielenia pomnóż przez 3, dodaj następną cyfrę, podziel przez 7;
– resztę z dzielenia pomnóż… itd. Ostatnim działaniem będzie dodanie ostatniej cyfry.
Przykład:
3465 -> (3*3+4)/7 -> (6*3+6)/7 -> 3*3+5=14

d) …różnica między  testowaną liczbą, z której usunięto ostatnią cyfrę, a dwukrotnością usuniętej cyfry.
Przykład:
1022 -> 102 – 4 = 98

e) … Tę cechę proszę odgadnąć, czyli ustalić, na czym polega, na podstawie przykładu:
546 -> 35463 -> 21

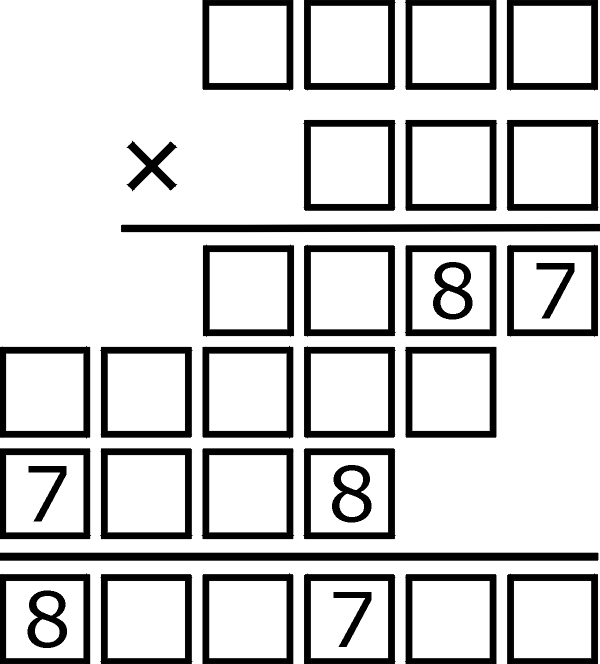
A na deser dla uczczenia przełomu lipca (7) i sierpnia (8) proponuję rozszyfrować mnożenie, w zapisie którego cyfry zastąpiono kratkami; ujawnione są tylko trzy siódemki i trzy ósemki.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3-4 dni.

Komentarze

[Antyp]

Zadanie dość proste, wystarczy zauważyć, że ostatnia cyfra mnożnika musi być równa 1 lub 3, a dalej jak po sznurku.
1887×471=888777

[asia]

Oj, znow, po wielu latach przerwy, uzalezniam sie od Pana lamiglowek 🙂 Uwielbiam je!

Zaczne od tego, ze wydaje mi sie, ze regula podzielnosci (c) jest calkowicie rownowazna regule z Wikipedii. Dzielimy od razu, i w pozostalej czesci obliczen rozpatrujemy jedynie reszte z dzielenia. Sporo upraszcza dzialania.

Reguly (e) jeszcze nie zgadlam… (O ile to tez ma byc cecha podzielnosci przez 7, a nie przez np. 3… ;)) Jakos myli mnie 35463->21 – sugeruje dodawanie cyfr, ktore z zalozenia dla 7 nie ma sensu. Wiec jesli to rzeczywiscie chodzi o dodawanie, to magia musi lezec w tych dwoch 3. Bede jeszcze kombinowac.

I dzialanie: 1887 x 471=888777

Pozdrawiam!

[witman]

1887*471=888777

[bd]

1887
471
1887
13209
7548
888777

[jawa]

1887×471=888777
e) może tak-liczbę trzycyfrową uzupełniamy jedną cyfrą przed liczbą, drugą cyfrą za liczbą tak, by liczby dwucyfrowe: ta utworzona z I i II cyfry oraz ta utworzona z IV i V cyfry były podzielne przez 7. Jeśli suma cyfr liczby pięciocyfrowej dzieli się przez 7, to i liczba trzycyfrowa dzieli się przez 7?

[andy]

Rachunki: 471×1887=888777
Cecha: dopisujemy na poczatku i na koncu takie cyfry, aby liczba dwucyfrowa na poczatku i na koncu byla podzielna przez 7. Jak suma cyfr takiej nowej liczby dzieli sie przez 7, to stara liczba tez.
Ale to dziala tylko dla liczb 3-cyfrowych.
a