Piątka do kwadratu

11 grudnia 2021
Marek Penszko

Łącząc całymi bokami na wszystkie możliwe sposoby pięć jednakowych kwadratów, można utworzyć tuzin różnych wielokątów – każdy z nich i cały ten komplet zwany jest pentominem. Wielokąty mają też literowe nazwy – w zależności od tego, z jaką literą kojarzy się kształt każdego z nich. Tyle gwoli przypomnienia.
Ilu różnych solistów należy wybrać z zespołu pentomina, aby ułożyć z nich kwadrat? Możliwość jest oczywiście tylko jedna – 5, ponieważ 5^2=25. Wzór na kombinacje bez powtórzeń pozwala ustalić, że 5 wielokątów z 12 można wybrać na 792 sposoby. Jednak nie każda piątka zaowocuje kwadratem – takich piątek jest tylko 47, natomiast różnie ułożonych kwadratów 107, bo niektóre piątki dadzą się poskładać w kwadrat na więcej niż jeden sposób. Najbardziej owocny jest kwintet ILPWY, a jeden z kwadratowych okazów splecionych z tej piątki wygląda tak:

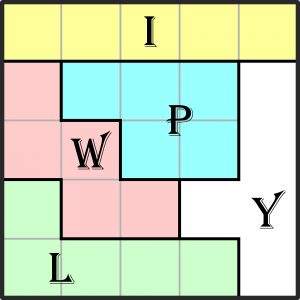
Układ ten jest jako okaz znamienny tym, że jeden z wielokątów (P) stanowi enklawę szczelnie otoczoną trzema i tylko trzema innymi obszarami, a w związku z tym stanowi jakby wizualizację twierdzenia o czterech barwach.
Nieco osobliwy jest także poniższy układ – jedyny w którym „W” dotyka brzegu tylko jednym kwadratem.

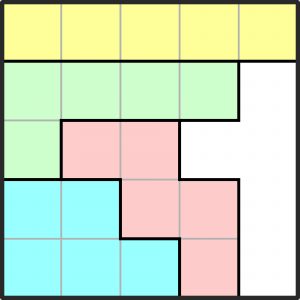
Inne kwadratowe układy z wielokątów ILPWY chyba niczym się nie wyróżniają. A ile ich jest wszystkich różnych? – oto jest pytanie (te, które powstają z innych w wyniku obrotów i/lub odbić lustrzanych uznajemy oczywiście za jednakowe). Odpowiedź znajduje się w grudniowym Świecie Nauki, ale nie polecam jej jako ściągawki, bo jest… błędna.

Komentarze z prawidłowym rozwiązaniem ujawniane są wieczorem w przeddzień kolejnego wpisu (z błędnym zwykle od razu). Wpisy pojawiają się co 7 dni.