Co jeszcze?
Łamigłówki indukcyjne są rozrywkowe inaczej, więc kuszą głównie wybrańców. Mimo tego ograniczenia od czasu do czasu ryzykuję ich wpadanie do Łamiblogu. Poprzednia była przed ponad rokiem, więc pora podręczyć Państwa kolejną.
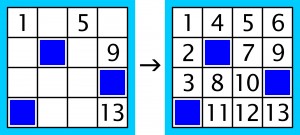
Przykład z rozwiązaniem – oczywiście jedynym możliwym – wygląda tak:
Z przykładu należy wywnioskować, jakie są zasady zabawy, a następnie, korzystając z nich, rozwiązać poniższe zadanie.
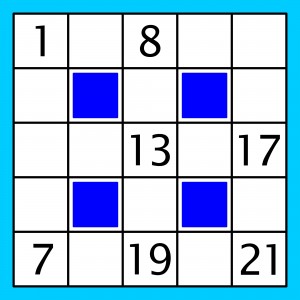
Łatwo ustalić, że w diagramie powinny się znaleźć liczby od 1 do n, gdzie n jest liczbą białych pól oraz że liczby w każdym wierszu i w każdej kolumnie muszą tworzyć ciąg rosnący. Ale co poza tym? Podpowiem, że dalszy ciąg reguł jest prosty, ale nieco kłopotliwy do sformułowania.

Komentarze
01_05_08_09_10
02____11____12
03_06_13_14_17
04____15____18
07_16_19_20_21
Liczby wpisałem zgodnie z pewnym „dalszym ciągiem reguł”, który jest „nieco kłopotliwy do sformułowania.”
🙂
mp
Moja nieśmiała próba:
http://s16.postimg.org/accek2clh/linia.png
Przepraszam…. idę spać 🙂 taki byk…. w moim „rozwiązaniu” 🙁
1,5,8,10,11
2,-,9,-,12
http://s23.postimg.org/aanrimj2j/2016_02_10_23_09_11_01.jpg
mam nadzieję, że dobrze. Poprzednio wpis się zepsuł, bo pisałem z komórki 🙁
To nie to, ale może zgodnie z jakąś regułą inną niż „firmowa”, pasującą do przykładu i zadania.
mp
… juz ułożyłem kilka reguł, które dają jedno jedyne rozwiązanie przykładu…
natomiast każda z tych reguł daje różne rozwiązania zadania głównego…
(choćby, próba z mojego poprzedniego postu)
Mnogość reguł, które można stworzyć, wynika pewnie ze skąpości przykładu, do którego łatwo znaleźć jakąś dodatkową regułę, a która jest niestety odmienna od zamysłu autora.
Nie będę tu strzelał kolejnymi rozwiązaniami, bo mi samemu się one nie podobają, szukam dalej tej jednej jedynej… ładnej reguły 🙂
Rozwiązałem „po swojemu” zadanie, patrzę, a to dokładnie to, co zaproponował @apartado… Reguła jest „prosta, ale kłopotliwa do sformułowania”, mimo to spróbuję. Założenie jest takie wstępne, że liczby już wpisane są zadane z góry i do żadnych reguł stosować się nie muszą. Pozostałe liczby wpisujemy następująco: najpierw ile się da pionowo w dół w lewej kolumnie. Następnie od góry rzędami w prawo, tak aby spełniona była monotoniczność. Czyli 5 między 1 a 8, dalej 6 za 8 się nie da, i nie da się też w drugim rzędzie, więc pierwsze (i zarazem jedyne) pole gdzie można wstawić 6 jest w rzędzie 3. po lewej stronie 13. Dalej 9 i 10 na górze, 11 pod 8, 12 pod 10, 14 za 13, 15 pod 13, a 16 musi być między 7 a 19. 18 i 20 wiadomo. Reguła „najpierw ile się da pionowo w dół w lewej kolumnie, a następnie od góry rzędami w prawo, tak aby spełniona była monotoniczność” działa oczywiście w przypadku diagramu górnego przykładowego.
Czyli „cel uświęca środki”. Gdybyż jeszcze środki były zwięzłe i eleganckie. Obawiam się, że to najtrudniejsze z dotychczasowych zadań indukcyjnych.
mp
1,5,8,9,10
2,X,11,X,12
3,6,13,14,17
4,X,15,X,18
7,16,19,20,21
Jak będzie dobrze to spróbuję opisać regułę a jak źle to po co się męczyć 🙂
Ale może reguła, choć inna, jest ładna i da się zamknąć w jednym zdaniu niezbyt wybujałym.
mp
Ostatnia próba (to wydaje mi się najlepsze z tych co wymyśliłem):
1,5,8,10,11
2,–,9,–,12
3,6,13,15,17
4,–,14,–,18
7,16,19,20,21
Marudzilem juz, ze nie lubię szachów, to teraz pomarudze, że zadań indukcyjnych tez nie lubię! 🙂
To ja pomarudzę, że też niezbyt lubię, ale…muszę, bo drażni mnie, gdy nie mogę rozgryźć reguł zadania w japońskim lub chińskim pisemku, a skorzystanie z googlowego tłumacza nie jest proste. No więc męczę się, korzystając z poszlak i pojedynczych słów, które jakimś cudem rozszyfrowuję. Ale za to jaka satysfakcja, gdy w końcu uda się osiągnąć cel.
mp
Chmmm… Takiej riposty się nie spodziewałem…
A nie prościej byłoby zaprzyjaźnić się z jakimś Japończykiem / Chińczykiem, który wspomógłby od czasu do czasu? 🙂
Jest taka znajomość i możliwość, ale korzystam z niej w ostateczności (dotąd zdarzyło się tylko raz), bo to przyznanie się do porażki. Sporą frajdą jest rozgryźć coś po paru tygodniach prób. To jak złamanie sekretu Enigmy 🙂 .
mp
01_04_08_10_11
02____09____12
03_06_13_14_17
05____15____18
07_16_19_20_21
Wszystkie diagonalne ciągi też są rosnące/malejące.
Przykład był rozwiązaniem jedynym możliwym – tu tak nie jest, ale i tak odczuwam jakąś, trudną do sformułowania satysfakcję.
To już coś, bo jakby pomysł na nowe zadanie.
Oryginalna reguła jest wprawdzie z całkiem innej parafii, ale rozwiązanie „firmowe” spełnia podany warunek, czyli rosnących ciągów ukośnych (prawoskośnych).
mp
A da się tak ułożyć diagram, żeby jakaś diagonalna nie była rosnąca, jeśli wiersze i kolumny są?
To jest tzw. dobre pytanie 🙂
mp
@ Wiąz
W moim pierwszym „rozwiązaniu” pomiędzy 9 a 4 nie jest spełniona reguła „rośnie albo spada”.
Ergo – można ułożyć taki diagram.
Wiąz,
Pytanie dotyczy diagramu z zadania, czy to pytanie ogólne?
Jeśli pierwszego, to wystarczy wziąć ostatni przykład apartado i zamienić miejscami 5 i 6.
A ogólnie, to można nawet wymyślić taki diagram:
1__
_3_
__2
Pomyślę jeszcze nad mniej trywialnym przykładem zaburzającym przekątną o tym kierunku.
Jeszcze takie pytanie: przez diagonalną rozumiecie tylko te linie, które nie zawierają pustych kratek? U apartado jest linia 7-13-11 – celowo, czy przypadkiem?
@Wiąz:
Diagonale idące z lewej góry do prawego dołu oczywiście muszą być rosnące.
Ale te idące z lewego dołu do prawej góry wcale nie muszą.
Podałbym przykład, ale nie mam obecnie możliwości. Proponuje samemu ułożyć diagram przykładowy z główna przekątna od lewego dołu z wartościami 6, 8, 7. To nie jest trudne, a przeczy postawionej tezie 😉
@Wiąz:
Ach.. Teraz mnie olśniło…
W rozwiązaniu przykłady o rozmiarach 4×4 wystarczy zmienić miejscami 6 i 7, i już teza o rosnących przekątnych obalona!
Diagonalna musi mieć zwrot taki, jaka jest monotoniczność wierszy i kolumn.
Przykłady z postów powyżej każą iść pod prąd: kolumna z góry na dół zaś wiersz z prawej na lewą :-). Założenie zadania jest w skrócie takie, że idziemy z lewego górnego rogu do prawego dolnego. I nie potrzebna jest nam diagonalna, może być dowolna łamana (z zachowaniem zwrotu poruszania się).
@Wiąz:
Właśnie sobie uświadomiłem, że nawet przekątna z lewej góry idąca do prawego dołu nie musi być rosnąca!!!
Jednak aby tak było, puste pola muszą mieć odpowiedni rozkład.
Poniżej przykład, który powinien rozwiać wątpliwości:
124
37X
5X6
@miodziu i tu mnie masz, przyznaję! 🙂 Brawo!
„Pomyślę jeszcze nad mniej trywialnym przykładem zaburzającym przekątną o tym kierunku.”
Jak powiedział, tak, o dziwo, zrobił (pewnie dlatego, że nie było o to trudno).
Modyfikuję diagram z zadania (dodaję pustą kratkę na środku) i wypełniam liczbami tak:
1__2__3__4__5
6____12____17
7_10____11_18
8____13____19
9_14_15_16_20
2-12-11-19
Warunkiem koniecznym* (czy wystarczającym*?) jest istnienie dwóch kratek A i B leżących na wspólnej diagonalnej, z których A jest bliżej lewego górnego rogu i jednocześnie nie istnieje ścieżka z A do B wykorzystująca ruchy wyłącznie w dół lub w prawo przez kratki z liczbami. Czyli u mnie np. A=12, B=11.
*by pusty diagram dało się wypełnić zaburzając rosnącość którejś prawoskośnej diagonalnej.
Właściwie to powinno być tak:
01_05_08_10_11
02_XX_09_XX_12
03_06_13_14_17
04_XX_15_XX_18
07_16_19_20_21
wszystkie górne przekątne typu / są rosnące
wszystkie dolne przekątne typu / są malejące
środkowa przekątna typu / do połowy od połowy maleje
wszystkie przekątne typu \ rosną
Problem w tym, że jak zamienimy 4 z 5 to też mamy dobre rozwiązanie według tych reguł skąd wniosek, że nie o to chodzi 🙂
Melduję, że w zagadce indukcyjnej każde rozwiązanie jest poprawne!
To ja zamelduję, że zagadka ma tylko jedno rozwiązanie, tzn. jedną regułę dającą jedno rozwiązanie.
Chyba że ktoś znajdzie drugą taką jednoznaczną regułę 🙂
mp
Kiedy już nadejdzie ta wiekopomna chwila – ujawnienie rozwiązania, proponuję zrobić to w dwóch posunięciach:
1. ujawnienie zawartości diagramu…
i powiedzmy dzień później:
2. ujawnienie magicznej formuły
według mnie będzie ciekawie 😉
Żeby było jeszcze ciekawiej, proponuję:
– zawartość diagramu ujawnię dokładnie w tym miejscu za dni parę
– „magiczna formuła” pojawi się w… czerwcu w letnim „Omnibusie” (będzie w nim kilka takich zadań), choć niewykluczone, że po ujawnieniu rozwiązania, ktoś sam ją odkryje.
mp
Rozwiązanie zadania
bez reguły podania:
01_04_08_09_10
02____12____16
03_06_13_15_17
05____14____18
07_11_19_20_21
mp
A może:
1,2,8,10,11
3,-,9,-,12
4,5,13,14,17
6,-,15,-,18
7,16,19,20,21
??
No, proszę! Niech to będzie dobrze!!! 🙂
Przykro mi… Zaraz wkleję „dobrze” pod ostatnim wpisem apartado
mp
Ktoś rozwiązał? Gdzie jest komentarz 190898? 🙂
Nikt nie rozwiązał. Rozwiązanie zadania zamieściłem pod ostatnim wpisem apartado.
Komentarz 190898 albo był spamem, albo usunąłem na prośbę komentatora (nie pamiętam dokładnie). Na podobnej zasadzie „zniknął” komentarz 190892.
mp