Czary-mary
Uprzedzam i z góry przepraszam zaawansowanych główkołamaczy – tym razem będzie nieco infantylnie.
Dzieci uwielbiają sztuczki – oglądać i pokazywać, nierzadko nawet bardziej to drugie. Lubią także bawić się liczbami. Maciek, ośmioletni syn moich sąsiadów, wie o mojej słabości do łamigłówek.
– Wujku, pomyśl sobie jakąś liczbę od 1 do 10.
– Pomyślałem.
– Pomnóż ją przez dwa.
– Już.
– Dodaj dziesięć.
– Gotowe.
– Weź połowę tego, co otrzymałeś.
– Mam połowę.
– Dodaj cztery.
– Dodane.
– Odejmij tę liczbę, którą pomyślałeś na początku.
– Już odjąłem.
– Wiem, ile ci wyszło – dziewięć.
– Nie.
– Eee… Jak to?
– Żartowałem, oczywiście że dziewięć.
– Hurra! Fajna sztuczka, co nie?
Takie liczbowe odgadywanki były popularną rozrywką już w XVII wieku. Wśród warstw nieoświeconych uchodziły za przejaw umiejętności niemal czarnoksięskich. Dziś uznajemy je za trywialne, choć nie zawsze ich sekret łatwo jest rozszyfrować.
Pytanie kobiety o lata to oczywiście gruby nietakt, ale można go odchudzić prosząc damę, aby podzieliła swój wiek przez 3, przez 5 i przez 7, podała resztę z każdego dzielenia i… już wiadomo, ile pani liczy sobie wiosen. Wystarczy skorzystać z tzw. chińskiego twierdzenia o resztach – jednego z fundamentalnych w teorii liczb. A twierdzenie to ma blisko dwa tysiące lat.
Jeżeli liczby całkowite dodatnie A, B, C spełniają warunki:
– A jest większe od B, a B większe od C,
– A jest mniejsze od iloczynu B i C,
– B i C nie mają wspólnych podzielników większych od jednego,
wówczas liczba A jest jednoznacznie określona przez parę liczb, z których jedna jest resztą z dzielenia A przez B, a druga resztą z dzielenia A przez C.
Oszczędzę Państwu dłuższych wywodów, podam tylko wzór końcowy, z którego należy skorzystać, aby określić wiek – będzie on równy reszcie z dzielenia:
(70x + 21y + 15z) : 105
gdzie x, y, z są resztami z dzieleń lat delikwenta odpowiednio przez 3, 5 i 7. Proszę sprawdzić na sobie, że wzór „działa”.
Wypada, aby wujek czymś się zrewanżował. Poprosiłem Maćka o przygotowanie kwadratowej kartki, podzielenie jej liniami na 16 małych kwadratów i wpisanie w kwadraty kolejno liczb od 1 do 16. Poprosiłem także, by przez chwilę pobawił się zginając kartkę – kilkakrotnie wzdłuż każdej oznaczonej linii, w obie strony, aby zgięcia się „wyrobiły”.
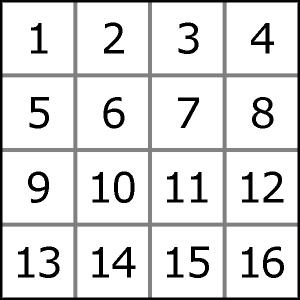
Po paru minutach Maciek zjawił się z ponadginaną kartką.
– Może być?
– W porządku. Teraz zacznij składać kartkę. Dowolnie, byle wzdłuż oznaczonych linii. Możesz złożyć ją na pół, potem znów na pół i tak dalej, ale możesz także zagiąć na początku jeden rząd kwadratów, potem znowu jeden rząd – dłuższy lub krótszy… Wszystko jedno, wzdłuż której linii i w którą stronę, byleby na końcu, czyli po czterech zgięciach, powstała składka w postaci małego, grubaśnego kwadracika.
Maciek kombinował przy składaniu, pytając się za każdym razem, czy tak wolno. W końcu ścisnął finalny kwadracik. Dałem mu nożyczki.
– Zmniejsz kwadratową składkę, obcinając jej cztery boki. W ten sposób usuniesz wszystkie linie zgięć i składka rozpadnie się na szesnaście małych kwadracików, ale wciąż trzymaj je razem. A teraz połóż na stole i – nie odwracając żadnego – porozsuwaj je tak, abyś widział wszystkie. Na niektórych zobaczysz liczby, na innych nie, bo będą leżały spodem do góry. Dodaj wszystkie widoczne liczby i odwróć karteczkę, którą umieściłem obok na stole.
Maciek spojrzał na mnie z niedowierzaniem, gdy okazało się, że obliczona suma i liczba zapisana na karteczce są równe.
– Wujku, jak to zrobiłeś?
– To nie ja. Samo wyszło. Zastanów się, dlaczego.
Ponieważ Maciek chodzi na lekcje angielskiego, zaproponowałem mu, aby zajrzał na tę stronę. Wspaniały iluzjonista i jego pomocnik prezentują tam liczbową sztuczkę-łamigłówkę, która nawet na starych koniach może zrobić spore wrażenie – dopóki jej trik nie zostanie ujawniony. Niektórzy, by nie pozbawiać się iluzji, wolą nie poznawać sekretu, choć jest on dziecinnie prosty.

Komentarze
Sztuczka na angielskiej stronie jest rzeczywiście bardzo fajna i robi wrażenie, jakby zwierzak-iluzjonista czytał w myślach internauty. Rozszyfrowanie jej sekretu to znakomita łamigłówka, ale istotnie dla dzieci po pierwszych lekcjach rachunków.
Fajna i prosta jest jeszcze sztuczka, ktora najlepiej pokazywac na kalkulatorze (albo lepiej kazac zrobic samemu):
Wymyśl liczbę 3-cyfrową, następnie napisz ją dwa razy (np. dla „123” piszemy „123123”). Podziel ją przez 7 (nie przejmujac sie reszta…), potem przez 11 (j.w.) i wreszcie przez 13… i voila -> wyszla pomyslana liczba!
Pieknie jest czytac tak mądre teksty pisane przez Ciebie.Hmmm……Intrygujesz mnie.Ale to chyba dobrze,wtedy świat jest ciekawszy.Myslisz,że wszystko w życiu jest wzorem matematycznym?Ciekawe jaki wzór Ty stosujesz?I czy się sprawdza?Pozdrawiam.Iwa.
jak to jest mozliwe w tym pierwszym ze wyjdzie ta liczba chcialabym sie dowiedziec prosze mi napisac na moj mail : margarita15@poczta.onet.pl
– Wujku, pomyśl sobie jakąś liczbę od 1 do 10.
– Pomyślałem. [x]
– Pomnóż ją przez dwa. [2x]
– Już.
– Dodaj dziesięć. [2x + 10]
– Gotowe.
– Weź połowę tego, co otrzymałeś. [x + 5]
– Mam połowę.
– Dodaj cztery. [x + 9]
– Dodane.
– Odejmij tę liczbę, którą pomyślałeś na początku. [9]
– Już odjąłem.
– Wiem, ile ci wyszło – dziewięć.
iwonkas-to dziala tak:
x-liczba trzycyfrowa
Jesli zapiszemy ja po sobie dwukrotnie to bedzie to 1001*x
1001x/13/7/11=1001x/(13*7*11)=1001x/1001=x
Masz dowod matematyczny
nie rozumiem z angielskim
Rany, mój kolega napisał kiedyś program do robienia podobnej sztuczki? Do pobrania wersja 2.0, napisana od zera przeze mnie: http://brunus.ovh.org/prg/optikal20.exe
Czy można zastosować inne liczby w pierwszym zadaniu? Zamiast dodawania 10 i 4.
Oczywiście, tylko wtedy na końcu „wyjdzie” inna liczba. Jaka? – wystarczy policzyć.
m
baaaaaaaaardzofaaaaaaaaaaaaajne
a jaka liczba była na karteczce którą odwrócił wujek ?????????????????