Ciąg 2D

25 października 2009
Marek Penszko

Na stronach poświęconych matematyce rekreacyjnej trafiam czasem na łamigłówki, które nazywam rasowymi. To te, z napoczęciem których mam problem. Nie wiem, jak je ugryźć, choć są zrozumiałe i w pierwszej chwili wydaje się, że kłopotu nie będzie. Takie zadania uważam za pięciogwiazdkowe, ponieważ najważniejsze to znaleźć na nie sposób, czyli wpaść na pomysł. Nie zawsze się to udaje, bo czasem wiedzy nie staje, czyli nie zna się jakiegoś twierdzenia, a częściej metody, zaś żeby samemu ją odkryć, nie staje intelektu.
Rasowość jest cechą względną – zgryz miewa nie każdy, a poza tym ten, kto ma, przy następnym podobnym zadaniu już mieć nie będzie. Można by jednak uznać za łamigłówki bezwzględnie rasowe te, które stawiają „pomysłowy” opór większości rozwiązujących.

Ostatnio na łamigłówkowym forum Gazety Wyborczej pojawiło się mało znane zadanie sprzed wielu lat (pierwszy opublikował je chyba Ross Honsberger w książce Ingenuity in Mathematics), które zaliczyłbym do rasowych, choć już nie dla mnie.

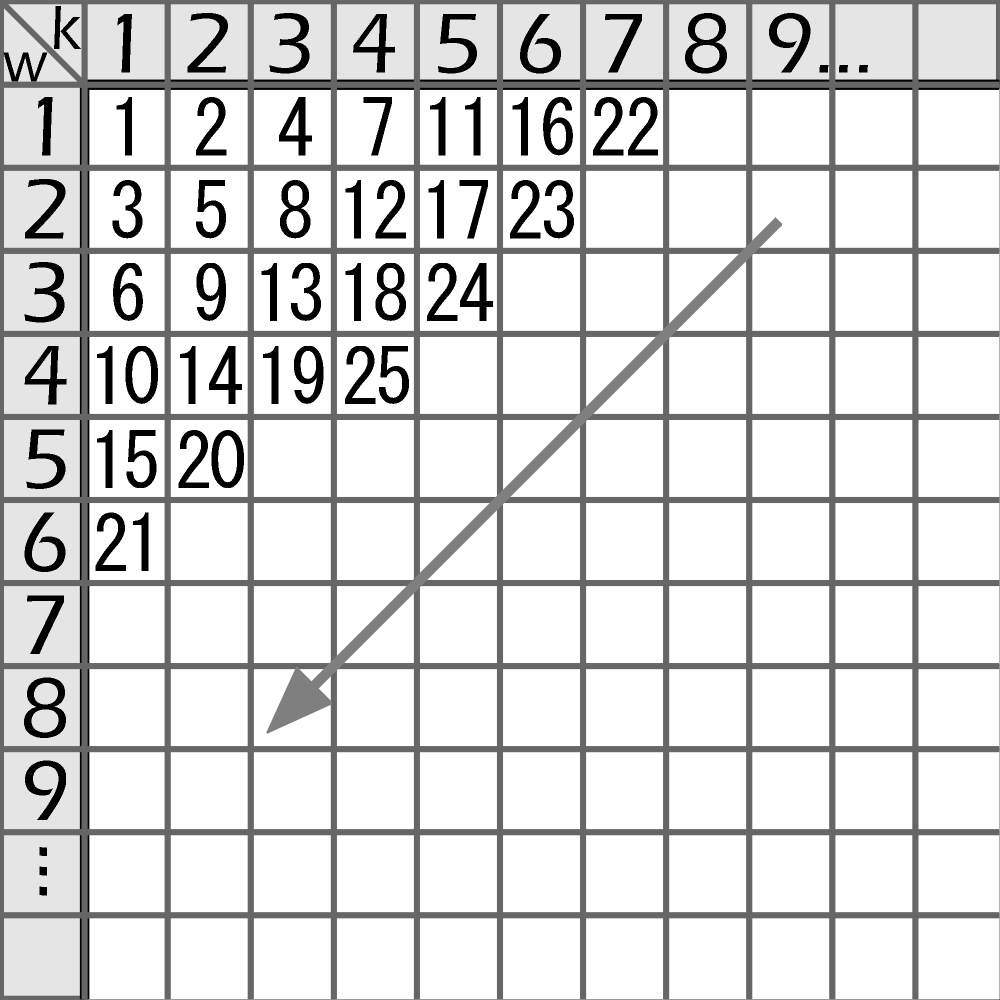
Do tabeli wpisany jest ciąg liczb całkowitych dodatnich – rzędami ukośnymi, zgodnie ze wskazaniem strzałki. Należy utworzyć wzór na wartość liczby w kolumnie k i w wierszu w. Inaczej mówiąc, chodzi o napisanie wzoru na wyraz ogólny ciągu dwuwymiarowego a(w,k). Na forum gazetowym podane jest rozwiązanie, ale o najważniejszym, czyli o sposobie dojścia do niego, nie wspomniano.

Z zadaniem trudno się uporać, nie znając metody tworzenia wzoru na ciąg, gdy znamy jego początkowy fragment. Pozwolę sobie zatem przedstawić stosowaną w takich przypadkach praktyczną metodę różnic skończonych. W odniesieniu do ciągów nie wygląda ona tak „strasznie” jak w Wikipedii. Przeciwnie, jest raczej rozrywkowa.

Weźmy ciąg z głównej przekątnej tabeli na powyższym rysunku, czyli:
1, 5, 13, 25, 41, 61, 85, …
Tworzymy ciąg różnic między jego kolejnymi wyrazami, potem ciąg różnic między różnicami, następnie ciąg różnic między różnicami między różnicami itd. – dotąd, aż pojawią się zera.

1___5___13___25___41___61
__4___8____12___16__ 20___ (pierwsze różnice)
____4____4____4____4______ (drugie różnice)
______0_____0___ 0_________ (trzecie różnice)

Gdyby już pierwsze różnice były zerowe, to wzór nie zawierałby zmiennych, czyli miałby ogólną postać:
a(n) = c, gdzie c jest jakąś stałą.
Przykład: c = 5; ciąg – 5, 5, 5, 5…
Przy zerowym ciągu drugich różnic wzór wyglądałby tak:
a(n)= bn + c (b i c to stałe).
Przykład: b = 2, c = 3; ciąg – 5, 7, 9, 11.
Gdy – jak w naszym przypadku – zerowe są trzecie różnice, to wzór będzie miał postać:
a(n) = an^2 + bn + c.
Warto zwrócić uwagę, że stopień wielomianu jest zawsze o jeden mniejszy od numeru rzędu, w którym pojawiły się różnice zerowe.
Wracając do naszego przykładu, korzystamy z ostatniego wzoru, aby obliczyć stałe a, b, c. W tym celu kolejno podstawiamy pod n wartości 1, 2, 3; w każdym przypadku wynik powinien być równy odpowiedniemu wyrazowi ciągu, czyli:
Jeśli n = 1, to a(n) = 1, czyli a + b + c = 1
Jeśli n = 2, to a(n) = 5, czyli a + 2b + 4c = 5
Jeśli n = 3, to a(n) = 13, czyli a + 3b + 9c = 13
Z układu trzech równań z trzema niewiadomymi obliczamy wartości a, b, c: a = 1, b = -2, c = 2. Podstawiając je do ogólnego wzoru otrzymujemy wzór na nasz ciąg:
a(n) = 2n(n – 1) + 1.

Znając metodę, można przystąpić do rozwiązywania zadania, tworząc najpierw wzór na pewien ciąg, a potem, dedukując, dotrzeć do celu.

Na forum pojawiło się pytanie o współrzędne w i k liczby 2009. Jak dotąd pozostaje bez odpowiedzi. Może ktoś z Państwa spróbuje jej udzielić.

A gdyby to zadanie było dla kogoś za proste, proponuję zastanowić się nad podobnym, które różni się od powyższego tylko sposobem rozmieszczania liczb w diagramie – też rzędami ukośnymi, ale „wężykiem”. Póki co dla mnie jest to twardy „pomysłowy” orzech do zgryzienia, czyli łamigłówka rasowa.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co 3 dni.