Macki zdystansowane

5 maja 2013
Marek Penszko

Przygotowuję artykuł o mackach, a w związku z tym macam tu i ówdzie w poszukiwaniu różnych odmian tej łamigłówki, która rozkwitała w Japonii na początku lat 90., a potem ustąpiła miejsca sudoku. W oryginale nosiła śliczną jakby onomatopeiczną nazwę uororojikku, co znaczy ścianki logiczne, ale na świecie przechrzczono ją na tuzin sposobów – od kiełkujących linii przez cztery wiatry do sieci promieni i wreszcie macek. Krótko przypomnę zasady tej łamigłówki.

Liczby w kratkach mogą wysuwać macki (linie) w czterech kierunkach – w wierszach i kolumnach. Wartość każdej liczby oznacza, ilu pustych kratek w sumie liczba może i powinna sięgnąć mackami. Należy narysować wszystkie macki tak, aby „omacały” wszystkie puste kratki. Ponieważ pustych pól w diagramie jest dokładnie tyle, ile wynosi suma wszystkich liczb, zatem każdego pola może sięgnąć tylko jedna macka i żadna nie pomaca innej cyfry.
Przykład:

W tureckim piśmie dla główkołamaczy Akil oyunlari trafiłem na oryginalną odmianę macek – skrzyżowanie tego zadania z innym zwanym dystansami.
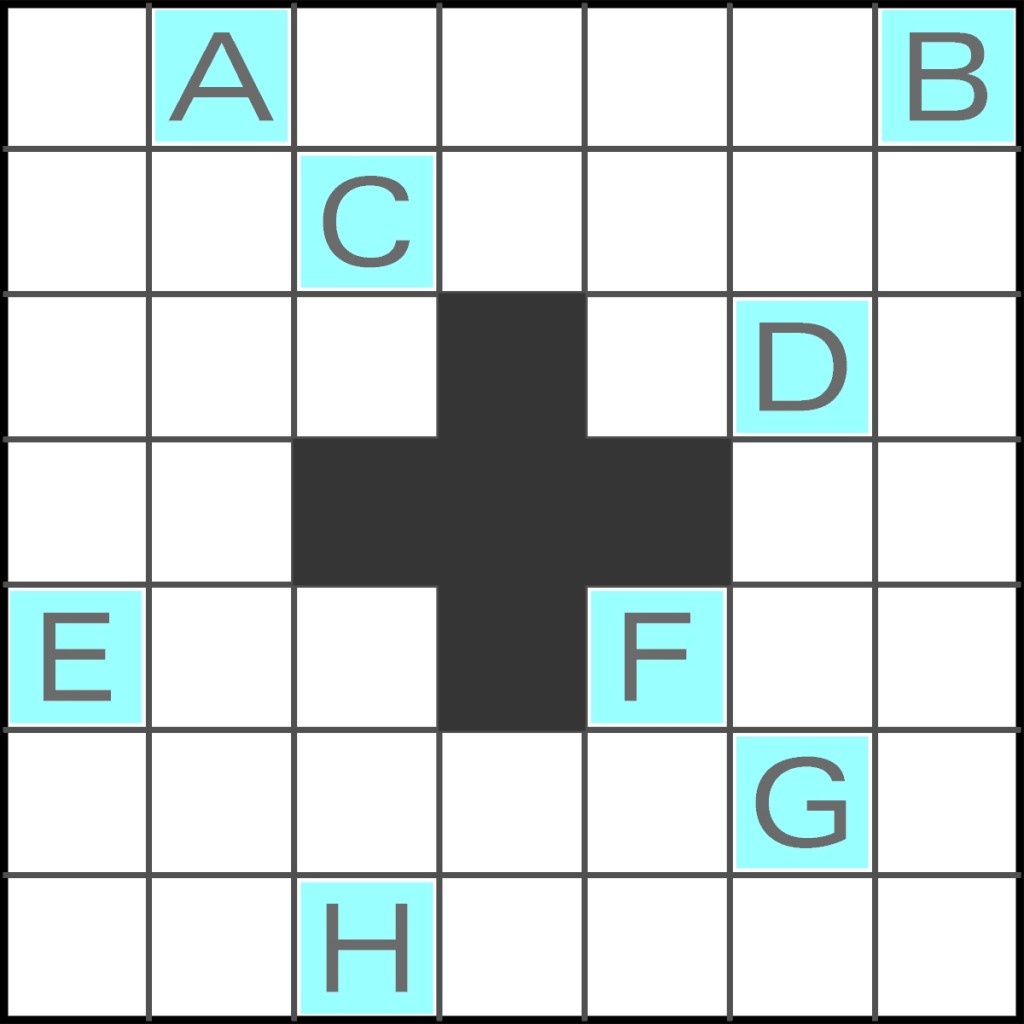
W diagramie oznaczonych jest n pól (niebieskie) – wszystkie, w których znajdują się liczby wysuwające macki. Liczby te są jednak niewidoczne. Ich wartości trzeba ustalić, wiedząc, że są one różne i kolejne – od 1 do n. Kluczem do tego jest reguła dystansów: odległość między każdą parą kolejnych liczb (a ściślej – między środkami pól z liczbami) powinna być większa niż między poprzednią. Inaczej pisząc: od 1 do 2 < od 2 do 3 < od 3 do 4 < … < od (n-1) do n.
Przykład macek zdystansowanych:

Pomysł jest ciekawy ze względu na sprzężenie obu rodzajów zadań, tzn. reguły jednego i drugiego stosuje się przy rozwiązywaniu na przemian – skorzystanie z jednych umożliwia zastosowanie drugich i odwrotnie. Proszę przekonać się o tym samemu, rozwiązując poniższą łamigłówkę.

W rozwiązaniu wystarczy podać, jakie liczby (od 1 do 8 ) odpowiadają poszczególnym literom.
Autorem zadania jest serbski łamigłówkarz Nikola Zivanovic.

Komentarze z prawidłowymi rozwiązaniami uwalniane są wieczorem w przeddzień kolejnego wpisu. Wpisy pojawiają się co kilka dni.